高考数学《回归课本》(二上)
一、选择题
1、下列命题中正确的是
(A) ac2>bc2 Û a>b (B)
a>b Û a3>b3
(C) Û a + c>b + d (D) loga2<logb2<0 Û 0<a<b<1
2、如果关于x的不等式ax2 + bx + c<0的解集是(m<n<0),则关于x的不等式cx2-bx + a>0的解集是 (二上31页B组7)
(A) (B)
(C) (D)
3、若x<0,则2 + 3x + 的最大值是
(二上11页习题4)
(A) 2 + 4 (B)
2±4 (C)
2-4 (D)
以上都不对
4、已知目标函数z=2x+y,且变量x、y满足下列条件: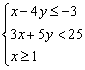 ,则(广州抽测)
,则(广州抽测)
(A) z最大值=12,z无最小值 (B) z最小值=3,z无最大值
(C) z最大值=12,z最小值=3 (D) z最小值=![]() ,z无最大值
,z无最大值
5、将大小不同的两种钢板截成A、B两种规格的成品,每张钢板可同时解得这两种规格的成品的块数如下表所示:
| 规格类型 钢板类型 | A规格 | B规格 |
| 第一种钢板 | 2 | 1 |
| 第二种钢板 | 1 | 3 |
若现在需要A、B两种规格的成品分别为12块和10块,则至少需要这两种钢板张数(广州二模)
(A)6 (B)
7 (C) 8 (D) 9
6、
函数f(q ) = 的最大值和最小值分别是(二上82页习题11)
(A) 最大值 和最小值0
(B) 最大值不存在和最小值
(C) 最大值 -和最小值0 (D) 最大值不存在和最小值-
二、填空题
7、当点(x,y)在以原点为圆心,a为半径的圆上运动时,点(x + y,xy)的轨迹方程是_______。
(二上89页B组10)
8、过抛物线y2 = 2px(p>0)的焦点F的直线与抛物线相交于A、B两点,自A、B向准线作垂线,垂足分别为A/、B/。则∠A/FB/ = _________。 (二上133页B组2)
9、 人造地球卫星的运行轨道是以地心为一个焦点的椭圆。设地球半径为R,卫星近地点、远地点离地面的距离分别是r1,r2,则卫星轨道的离心率 = _________。(二上133页B组4)
10、已知a>b>0,则a2 + 的最小值是_________。16 (二上31页B组3)
三、解答题
11、两定点的坐标分别为A(-1,0),B(2,0),动点满足条件∠MBA = 2∠MAB,求动点M的轨迹方程。(二上133页B组5)
12、设关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,已知
,已知![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
13、已知△ABC的三边长是a,b,c,且m为正数,求证 + > 。(二上17页习题9)
回归课本二下参考答案
一、选择题 1~6 BAC(注意符号)B(注意虚实)B(注意整点)A(注意横纵坐标不要搞颠倒)
二、填空题
7、x2 = a2 + 2y(-a≤x≤a)
8、证明: 设A、B两点的坐标分别为(x1,y1)、(x2,y2),则A/(-,y1)、B/(-,y2)。
∴ kA/F·kB/F = ,
又 ∵ y1y2 = -p2 ,
∴ kA/F·kB/F = -1,
∴ ∠A/FB/ = 900 .
9、e =
10、解:由a>b>0知a-b>0,
∴ b(a-b) = ()2≤( )2 = 。
∴ a2 + ≥a2 + ≥2= 16。
上式中两个“≥”号中的等号当且仅当a2 = ,b = a-b时都成立。
即当a = 2,b = 时,a2 + 取得最小值16。
三、解答题
11、解:设∠MBA = a ,∠MAB = b (a >0,b >0),点M的坐标为(x,y)。
∵ a = 2b ,∴ tana = tan2b = .
当点M在x轴上方时,tana = -,tanb = ,
所以- = ,即3x2-y2 = 3。
当点M在x轴下方时,tana = ,tanb = ,仍可得上面方程。
又a = 2b ,∴ AM > BM .
因此点M一定在线段AB垂直平分线的右侧,所求的轨迹方程为双曲线3x2-y2 = 3的右支,且不包括x轴上的点。
12、解:![]() ;
;
![]() 时,
时,![]() ,
,![]() 时,
时,![]() 。
。
∴![]() 时,
时,![]() 。
。
13、证明:∵ f(x) = (m>0) = 1-在(0, + ¥)上单调递增,
且在△ABC中有a + b > c>0,
∴ f(a + b)>f(c),
即 > 。
又∵ a,b Î R*,
∴ + > + = ,
∴ + > 。
另解:要证+ > ,
只要证a(b + m)(c + m) + b(a + m)(c + m)-c(a + m)(b + m)>0,
即abc + abm + acm + am2 + abc + abm + bcm + bm2-abc-acm-bcm-cm2>0,
即abc + 2abm + (a + b-c)m2>0,
由于a,b,c为△ABC的边长,m>0,故有a + b> c,即(a + b-c)m2>0。
所以abc + 2abm + (a + b-c)m2>0是成立的,
因此 + > 。
已知关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() 。
。
(1)当![]() 时,求集合
时,求集合![]() ;
;
(2)若![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
解:(1)![]() 时,不等式为
时,不等式为![]() ,解之,得
,解之,得 ![]()
(2)![]() 时,
时,![]()
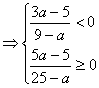
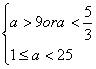
![]()
![]() 时,不等式为
时,不等式为![]() , 解之,得
, 解之,得 ![]() ,
,
则 ![]() , ∴
, ∴![]() 满足条件
满足条件
综上,得 ![]() 。
。