高考数学猜题2
一、定义A*B，B*C，C*D，D*B分别对应下列图形
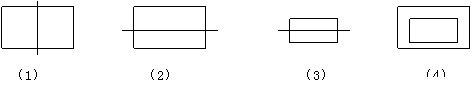
那么下列图形中
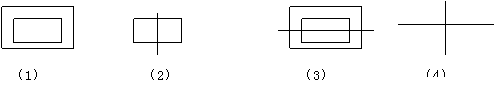
可以表示A*D，A*C的分别是 ( C )
A．（1）、（2） B．（2）、（3） C．（2）、（4） D．（1）、（4）
|
的焦点为F，相应于焦点F（c，0）（c>0）的准线l与x轴相交于点A，过点A的直线交双曲线于点P、Q，过P且平行于准线l的直线与椭圆交于另一点M，则M、F、Q三点共线。
|
证明：设
，
，则
，
|
|
|
|
|
|
且
，
设
，据题意
，
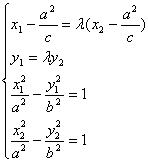
仿性质1的证明可得：
=
=（
）
=（
）
=
=
=
，
点F、M、Q三点共线。（证毕）
三、已知函数
的图像在点
处的切线与直线
平行.
⑴求a、b的值；
⑵求函数
的单调区间；
⑶求函数的在区间
上的最小值和最大值；
解： ⑴∵在的图像上， ∴
又
，
当
时，
⑵ 若
，则
或
∴分别在
和
上是增函数，在
上是减函数
⑶当
时，在区间上是减函数
当
时
当
时
当
时，在区间上是减函数，在
上是增函数
∴当或
时
当
时
当
时，在区间上是减函数，在
上是增函数且
这时当时；当时
四、已知双曲线
的实半轴长与虚半轴长的乘积为
为它的两焦点，过
的直线
与直线
的夹角
满足
与线段的垂直平分线交于点
与双曲线交于点
且
⑴求双曲线的方程；
⑵过点作一直线交双曲线的右支于两点M、N，问△
MN的面积是否有最小值？若有，求出最小值及此时直线MN的方程；若没有最小值，请说明理由.
解：⑴以所在直线为
轴，线段的垂直平分线为
轴，建立直角坐标系.
设所求的双曲线C的方程为
，则
由题意知，
∴
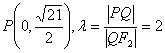
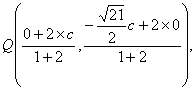即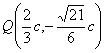
将点
代入双曲线C的方程，可得
，又
∴双曲线C的方程为
⑵设直线MN的方程为
则
将
代入双曲线C，得
∴
∴
=
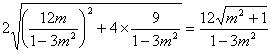
∴当
时，分母最大，分子最小，此时
最小值为12，MN⊥轴
即 MN的方程为=2