高考数学猜题4
1. 为防止某突发事件,有甲、乙、丙、丁四种相互独立的预防措施可供采用,单独采用甲、乙、丙、丁预防措施后此突发事件不发生的概率(记为P)和所需费用如下表:
| 预防措施 | 甲 | 乙 | 丙 | 丁 |
| P | 0.9 | 0.8 | 0.7 | 0.6 |
| 费用(万元) | 90 | 60 | 30 | 10 |
预防方案可单独采用一种预防措施或联合采用几种预防措施,在总费用不超过120万元的前提下,请确定一个预防方案,使得此突发事件不发生的概率最大.
解: 方案1: 单独采用一种预防措施的费用均不超过120万元.由表可知, 采用甲措施,可 使此突发事件不发生的概率最大,其概率为0.9.
方案 2: 联合采用两种预防措施, 费用均不超过120万元, 由表可知, 联合甲、丙两种预防措施可使此突发事件不发生的概率最大,其概率为:
1-(1-0.9)(1-0.7)=0.97.
方案3: 联合采用三种预防措施, 费用均不超过120万元,故只能联合乙、丙、丁三种预防措施,此时突发事件不发生的概率为 :
1-(1-0.8)(1-0.7)(1-0.6)=0.976.
综合上述三个预防方案可知, 在总费用均不超过120万元的前提下, 联合使用乙、丙、丁三种预防措施可使此突发事件不发生的概率最大.
2. 已知函数![]() =
=![]() (a,b
(a,b![]() ).
).
(1)若a=1,函数![]() 的图象能否总在直线
的图象能否总在直线![]() b的下方?说明理由;
b的下方?说明理由;
(2)若函数![]() 在【0,2】上是增函数,
在【0,2】上是增函数,![]() =2是方程
=2是方程![]() =0的一个根,求证:
=0的一个根,求证:
![]() ≤-2;
≤-2;
(3)若函数![]() 图象上任意不同的两点连线斜率小于1,求实数a的取值范围.
图象上任意不同的两点连线斜率小于1,求实数a的取值范围.
解;(1) 不能,取![]() =-1,则
=-1,则![]() =2+b>b,即存在点(-1,2+b)在函数图象上,且在直线
=2+b>b,即存在点(-1,2+b)在函数图象上,且在直线![]() b的上方;
b的上方;
(2) 由![]() =2是方程
=2是方程![]() =0的一个根,得
=0的一个根,得![]() =
=![]() ,即
,即![]() ,又
,又![]() ,令
,令![]() 即解
即解![]() 得两根为
得两根为![]() ,又函数
,又函数![]() 在【0,2】上是增函数,所以
在【0,2】上是增函数,所以![]()
![]() 2,即a≥3,
2,即a≥3,![]() =-1+a+b=-1+ a+8-4a=7-3a≤-2,即
=-1+a+b=-1+ a+8-4a=7-3a≤-2,即![]() ≤-2;
≤-2;
(3) 设函数函数![]() 图象上任意不同的两点
图象上任意不同的两点![]() ,
,![]() ,且
,且![]() ,由连线斜率
,由连线斜率![]() <1,可得
<1,可得![]() <
<![]() ,函数
,函数![]() 在R上是单调递减的,
在R上是单调递减的,![]() ,求导且导数值满足
,求导且导数值满足![]() ,即
,即![]() 在R上恒成立,所以
在R上恒成立,所以![]() ,解得
,解得![]() 。
。
3. 如图,过抛物线![]() 的对称轴上任一点P(0,
的对称轴上任一点P(0,![]() )(
)(![]() 作直线与抛物线交于A、B两点,点Q是点P关于原点的对称点,
作直线与抛物线交于A、B两点,点Q是点P关于原点的对称点,
(1)设点P分有向线段![]() 所成的比为
所成的比为![]() ,证明:
,证明:![]() ;
;
(2)设直线AB的方程是![]() ,过A、B两点的圆与抛物线在A点处有公共的切线,求圆C的方程。
,过A、B两点的圆与抛物线在A点处有公共的切线,求圆C的方程。
解:(1)由条件设直线AB方程为![]() ,代人抛物线方程得
,代人抛物线方程得![]() ①设A、B两点坐标分别是
①设A、B两点坐标分别是![]() 、
、![]() ,则
,则![]() 、
、![]() 是方程①的两根,∴
是方程①的两根,∴![]() ,又∵点
,又∵点![]() 分有向线段
分有向线段![]() 所成的比为
所成的比为![]() ,∴
,∴![]() 即
即![]() =
=![]() .又点Q是点P关于原点的对称点,故点Q的坐标为
.又点Q是点P关于原点的对称点,故点Q的坐标为![]() ,从而
,从而![]() .
.
![]() =
=![]() ,
,
![]() =
=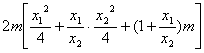 =
=![]()
∴![]() .
.
(2)
由![]() 且
且![]() 知点A、B坐标分别是(6,9)、(-4,4).
知点A、B坐标分别是(6,9)、(-4,4).
由![]() 知
知![]()
![]() ,
,![]() . ∴抛物线
. ∴抛物线![]() 在点A处的切线斜率为
在点A处的切线斜率为![]() .设圆C的方程为
.设圆C的方程为![]()
由![]() 解得
解得![]() .
.
![]() .∴圆C的方程为
.∴圆C的方程为![]() ,即
,即
![]() 为所求。
为所求。