高考数学第一轮总复习同步试卷
I卷 数列部分
一选择题（每题5分，共60分）
1、 某种细菌每半小时分裂一次（一个分裂为两个），经过3小时，这种细菌由1个可繁殖（ ）个
（A）8； （B）16； （C）32； （D）64；
2 已知
为等差数列，公差
，
，则
（ ）
(A). 60
(B). 
(C). 182 ( D). 
3、设{an}是由正数组成的等比数列，公比q=2，且a1a2a3…a30=230，则a3a6a9…a30等于（ ）
(A)210 (B)220 (C)216 (D)215
4、已知等比数列{an}，公比q=
且a1+a3+…+a49=30,则a1+a2+a3+…+a50=( )
A．35 B．40 C．45 D．50
5．数列
的前
项和为
，若
，则这个数列一定是（
）
A．等比数列 B．等差数列
C．从第二项起是等比数列 D．从第二项起是等差数列
6．等差数列中，已知前15项的和
，则
等于………（
）
A．
B．12 C．
D．6
7．等比数列{an}中，如果
，则
的值为……（
）
A．3 B．9 C．±3 D．±9
8．等差数列{an}中，
.记
，则S13等于（
）
A．168 B．156 C．152 D．78
9．在等比数列{an}中，
等于（ ）
A．
B．
C．
D．
10．已知Sn是等差数列{an}的前项和，若S6=36，Sn=324，Sn－6=144（n＞6），
则等于（ ）
A．15 B．16 C．17 D．18
11．设2a=3，2b=6，2c=12，那么数列
是（ ）
A.是等比数列，但不是等差数列 B．是等差数列，但不是等比数列
C．既是等比数列，又是等差数列D．不是等比数列，也不是等差数列
12．设
，则的值为（ ）
A．9 B．8 C．7 D．6
二、填空题（本大题共4小题，每小题4分，共16分）
13．一条信息，若一人得知后，一小时内将信息传给两人，这两人又在一小时内各传给未知信息的另外两人.如此下去，要传遍55人的班级所需时间大约为 小时
14．设数列{an}的前n项和为
15．观察数列的特点，并在空白处填上恰当的数：77，49，36，
. 16．等差数列{an}、{bn}的前n项和分别为Sn、Tn，若
的值为
.
高考第一轮总复习同步试卷(数列部分)答题卷
班级 姓名 学号 考分
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
13 14 15 16 。
三、解答题：(17—21题12分,22题14分,解答应写出文字说明、证明过程或演算步骤)
17．已知数列{an}的通项公式
，从{an}中依次取出第2项，第4项，第8项……第2n项
，按原来顺序排成一个新数列{bn}，求数列{bn}的通项公式及前n项和公式.
18.容器A中有12%的食盐水300克，容器B中有6%的食盐水300克.现约定完成下列工作程序为一次操作：从A、B两个容器中同时各取100克溶液，然后将从A中取出的溶液注入B中，将B中取出的溶液注入A中.
（1）经过n次操作后，A、B中的盐水浓度分别为an%、bn%，求证：an+bn为常数；
（2）分别求出an和bn的通项公式.
19．已知函数
，数列{an}满足：a1=1，且
（1）写出数列的前5项，并猜想数列
的表达式；
（2）若
，试求数列{bn}的前n项和Sn
.
20设an是正数组成的数列，其前n项和为Sn,且对所有自然数n,an与2的等差中项等于Sn与2的等比中项，求数列{an}的通项公式.
21．设函数
，数列的通项
满足
，⑴求数列的通项公式；⑵判定数列{a n }的单调性.
22.已知函数f(x)=(
)x+a的反函数f－1(x)的图象过原点.
（1）若f－1(x－3),f－1(－1),f－1(x－4)成等差数列，求x的值；
（2）若互不相等的三个正数m、t、n成等比数列，问f－1(m),f－1(t),f－1(n)能否组成等差数列，并证明你的结论.
参考答案
一,选择题
1D,2B,3B,4C,5A,6D,7B,8B,9A,10D,11B,12D.
二，填空题
13，5．14，67．15，18．16，
三解答题
17．
…………………………………………………4分
……12分
18（1）经过n次操作后，A中盐水的浓度为
，
得
，同理
.
为常数………6分
（2）由（1）可知
是首项为
，公比为
的等比数列，于是有
…………………13分
19．答案：（1）
，
故猜想数列的通项公式为：
；
（2）
20∵an与2的等差中项等于Sn与2的等比中项，∴
（an+2）=
,即Sn=
(an+2)2
当n=1时，a1=(a1+2)2
a1=2.
当n≥2时，an=Sn－Sn－1=［(an+2)2－(an－1+2)2］
即（an+an－1)(an－an－1－4)=0
又∵an+an－1>0,∴an=an－1+4,即d=4.
故an=2+(n－1)×4=4n－2.
21．解：⑴∵，又，
∴
令
，则
，∴
，
注意到，因此＝
， 
,
, ∴
即为数列的通项公式；
另解：由已知得
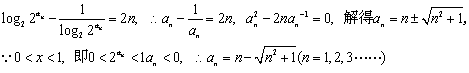
⑵
，可知数列是递增数列.
说明：数列是一类特殊的函数，判定数列的单调性与判定函数的单调性的方法是相同的，只需比较an+1与an的大小。
22 （1）∵f－1(x)图象过（0，0），可知原函数过（0，0）
∴有（）0+a=0a=－1
∴f(x)=()x－1,值域{yy>－1}
由y+1=()xx=log
(y+1)
∴f－1(x)=log(x+1)(x>－1)
∵f－1(x－3)=log(x－2),f－1(－1)=log=1,
f－1(x－4)=log(x－3)
∴log(x－2)(x－3)=()2=2
解得：x1=4,x2=1,
而又∵
x>3,∴x=4.
(2)假设f－1(m),f－1(t),f－1(n)组成等差数列，则有：
2log(t+1)=log(m+1)+log(n+1)
即(t+1)2=(m+1)(n+1)
化简得：2t=m+n①
又∵m、t、n成等比数列
∴t2=mnt=
代入①式
得2=m+n即（
－
)2=0
∴m=n,这与已知三数m、n、t互不相等矛盾.
∴f－1(m)、f－1(t)、f－1(n)不能组成等差数列.