高级中学高三数学第二次统测
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分．考试时间120分钟．
第Ⅰ卷（共60分）
一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1 .设集合
，则集合
等于
A．M
B．N C．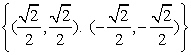
D.
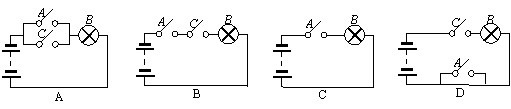2.在下列电路图中，表示开关A闭合是灯泡B亮的必要但不充分条件的线路图是
3．已知A是△ABC的一个内角，且
，则△ABC是
A．锐角三角形 B．钝角三角形 C．直角三角形 D．形状不确定
4．在100内能被3整除，但不能被7整除的所有正整数之和为
A．1368 B.1470 C.1473 D.1557
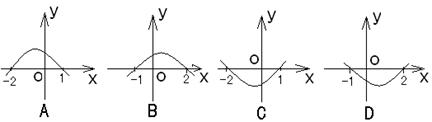5. 不等式
的解集为
，则函数
的图象为
6．某工厂投入98万元购买一套设备，第一年的维修费用12万元，以后每年增加4万元，每年可收入50万元．就此问题给出以下命题：①前两年没能收回成本；②前5年的平均年利润最多；③前10年总利润最多；④第11年是亏损的；⑤10年后每年虽有盈利但与前10年比年利润有所减少．（总利润=总收入－投入资金－总维修费）其中真命题是
A．①②⑤ B．①③⑤ C．①③④ D．②③④
7. 某人为了观看2008年奥运会，从2001年起，每年5月10日到银行存入a元定期储蓄，若年利率为p且保持不变，并约定每年到期存款均自动转为新的一年定期，到2008年将所有的存款及利息全部取回，则可取回的钱的总数（元）为
A．
B.
C.
D．
8．由2开始的偶数数列，按下列方法分组：（2），（4，6），（8，10，12），…，第n组有n个数，则第n组的首项为
A. n2-n B. n2-n+2 C. n2+n D. n2+n+2
9．将
的图像
A．先向左平行移动1个单位 B. 先向右平行移动1个单位
C．先向上平行移动1个单位 D．先向下平行移动1个单位
再作关于
对称的图像，可得函数
的图像.
10.已知函数f（x）对任意x, y∈R,都有f（x＋y）= f（x）＋f（y）,且f（1）＝2，
f（1）＋f（2）＋…＋f（n）(n∈N*)不能等于
A. 
f (1) B. f[] C. n (n+1) D. n (n+1)
f (1)
11.已知定义在R上的函数y=f(x)满足下列三个条件：
①对任意的x∈R都有
②对于任意的
，都有
③
的图象关于y轴对称．则下列结论中，正确的是
A．
B．
C．
D．
12．函数y=f(x)的图象是圆心在原点的单位圆的两段弧(如图)，则不等式f(x)＜f(-x)+x解为
A．{x-
＜x＜0或＜x≤1}
B．{x-1≤x＜-
或＜x≤1}
C．{x-1≤x＜-
或＜x≤1}
D．{x-＜x＜且x≠0}
第Ⅱ卷（非选择题共90分）
二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上
13. 等比数列
的首项
,前
项和为
若
，则公比
等于 .
14. 设函数
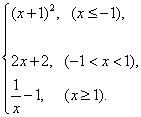已知
＞1，则
的取值范围是
.
15.设
， 则
…
的值为______ ___.
16. 数列
的前n项的乘积
，则的前5项的和是
.
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
17．（本小题满分12分）
已知f（x）=lg
．
（1）判断函数f（x）的奇偶性；
（2）求f- --1（lg2）．
18．（本小题满分12分）
已知等比数列{
}的公比为q，前n项和为Sn，是否存在常数c，使数列{
}也成等比数列？若存在，求出c的值；若不存在，说明理由.
19. （本小题满分12分）
某工厂去年的某产品的年产量为100万只，每只产品的销售价为10元，固定成本为8元. 今年，工厂第一次投入100万元（科技成本），并计划以后每年比上一年多投入100万元（科技成本），预计产量年递增10万元，第n次投入后，每只产品的固定成本为
为常数，
），若产品销售价保持不变，第n次投入后的年利润为
万元.
（1）求k的值，并求出的表达式；
（2）问从今年算起第几年利润最高？最高利润为多少万元？
20. （本小题满分12分）
函数
的定义域为
（
为实数）.
（1）当
时，求函数
的值域；
（2）若函数在定义域上是减函数，求的取值范围；
（3）求函数在
上的最大值及最小值，并求出函数取最值时
的值.
21．（本小题满分12分）
数列
.
（1）求数列
的通项公式；
（2）设Sn为的前n项和，并且有相同的n，使得Sn与
都取得最小值，
求实数a的取值范围.
22． （本小题满分14分）
如果函数
N*)满足
且
.
（I）求函数
的解析式；
（II）已知各项均不为零的数列
满足
（
为该数列的前项的和），求该数列的通项；
（III）如果数列满足
，求证:当
时，恒有
成立.