高考.数学模拟试题2
本试卷分第一卷（选择题）和第二卷（非选择题），共150分，考试时间120分钟．
一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．如图，点O是正六边形ABCDEF的中心，则以图中点
A、B、C、D、E、F、O中的任意一点为始点，与始点不
同的另一点为终点的所有向量中，除向量
外，与向量
共线的向量共有（
）
A．2个 B． 3个 C．6个 D． 7个
2．已知曲线C：y2=2px上一点P的横坐标为4,P到焦点的距离为5,则曲线C的焦点到准线的距离为 ( )
A． 
B． 1
C． 2
D． 4
3．若(3a2
－
) n 展开式中含有常数项，则正整数n的最小值是 （ ）
A．4 B．5 C． 6 D． 8
4． 从5名演员中选3人参加表演，其中甲在乙前表演的概率为 （ ）
A． 
B． 
C． 
D． 
5．抛物线y2=a(x+1)的准线方程是x=－3，则这条抛物线的焦点坐标是（ ）
A.（3，0） B.（2，0） C.（1，0） D.（-1，0）
6．已知向量ｍ＝（a，b），向量ｎ⊥ｍ，且｜ｎ｜＝｜ｍ｜，则ｎ的坐标可以为（ ）
A.（a，－b） B.（－a，b） C.（b，－a） D.（－b，－a）
7．已知函数f1(x)=x, f2(x)=
,f3(x)=4-x,函数g(x)取f1(x)、f2(x)、f3(x)中的最小值，则函数g(x)的最大值是（ ）
A. 2
B. 1 C. D. 不存在
8．有6个座位连成一排，现有3人就坐，则恰有两个空座位相邻的不同坐法有 （ ）
A．36种 B．48种 C．72种 D．96种
9．已知直线l、m，平面α、β，且l⊥α,m
β.给出四个命题：（1）若α∥β,则l⊥m;
(2)若l⊥m,则α∥β;(3)若α⊥β,则l∥m;(4)若l∥m,则α⊥β,其中正确的命题个数是( )
A.4 B.1 C.3 D.2
10．已知函数f(x)＝log2(x2－ax＋3a)在区间[2，＋∞)上递增，则实数a的取值范围是（ ）
A.(－∞，4) B.(－4，4] C.(－∞，－4)∪[2，＋∞) D.[－4，2)
11．4只笔与5本书的价格之和小于22元，而6只笔与3本书的价格之和大于24元，则2只笔与3本书的价格比较（ ）
A．2只笔贵 B．3本书贵 C．二者相同 D．无法确定
12．以下结论正确的是（ ）
A.
B.
C.
D. 
二、填空题：本大题共4小题，每小题4分，共16分．答案填在题中横线上．
13．.若sin2α＜0,sinαcosα＜0, 化简cosα
+sinα
=____________.
14．已知正三棱柱ABC—A1B1C1，底面边长与侧棱长的比为
∶1，则直线AB1与CA1所成的角为
。
15．某县农民年均收入服从μ=500元，
=20元的正态分布，则此县农民年均收入在500元到520元间人数的百分比为
．
16．
．
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
17．（12分）已知关于x的方程
有一根是2．
（1）求实数a的值；（2）若
，求不等式
的解集．
18．（本小题满分12分）
已知等差数列{an}中，a2=8，S10=185.
（Ⅰ）求数列{an}的通项公式an;
（Ⅱ）若从数列{an}中依次取出第2，4，8，…，2n，…项，按原来的顺序排成一个新数列{bn}，试求{bn}的前n项和An.
19．（本小题满分12分）
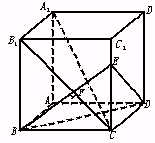已知长方体AC1中，棱AB＝BC＝3，棱BB1＝4，连结B1C，过B点作B1C的垂线交CC1于E，交B1C于F.
(1)求证A1C⊥平面EBD；
(2)求点A到平面A1B1C的距离；
(3)求平面A1B1C与平面BDE所成角的度数；
(4)求ED与平面A1B1C1所成角的大小；
20．（本小题满分12分）
某公司欲建连成片的网球场数座，用128万元购买土地10000平方米，该球场每座的建设面积为1000平方米，球场的总建筑面积的每平方米的平均建设费用与球场数有关，当该球场建x个时，每平方米的平均建设费用用f(x)表示，且f(n)=f(m)(1+
)(其中n＞m,n∈N)，又知建五座球场时，每平方米的平均建设费用为400元，为了使该球场每平方米的综合费用最省(综合费用是建设费用与购地费用之和)，公司应建几个球场?
21．（本小题满分12分）
已知定点Q（6，0）和抛物线y2=8x上的两个动点A（x1，y1）、B（x2，y2），其中A、B的横坐标x1、x2满足x1≠x2，且x1+x2=4．
（I）证明线段AB的垂直平分线过定点Q；
（Ⅱ）当A、B两点的距离为何值时，△AQB的面积最大？
22．（本小题满分14分）
设f(x)=ax2+bx+c(a＞b＞c),f(1)=0,g(x)=ax+b.
（1）求证：函数y=f(x)与y=g(x)的图象有两个交点；
（2）设f(x)与g(x)的图象交点A、B在x轴上的射影为A1、B1，求｜A1B1｜的取值范围；
（3）求证：当x≤－
时，恒有f(x)＞g(x).
．
参考答案
1 D; 2 A ; 3 B; 4 A ; 5 C; 6 C; 7 B; 8 C ; 9 D ; 10 B; 11 A ; 12 B .
13. 
sin(α－
); 14. 90°; 15 34.15% ; 16 
.
17．（1）用x=2代入原方程得
………………3分
………………5分
（2）
,………………7分
则原不等式化为
,………………9分
解之得
,即解集为
………………12分
18．本小题考查数列的基本知识和运算能力。
解：(Ⅰ)设{an}首项为a1,公差为d,
则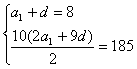
,解得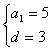
∴an=5+3(n-1),即an=3n+2 ……………… 6分
（Ⅱ）设b1=a2,b2=a4,b3=a8,
则bn=a2n=3×2n+2
∴An=(3×2+2)+(3×22+2)+…+(3×2n+2)
=3×(2+22+…+2n)+2n
=3×
+2n=6×2n-6+2n ……………… 12分
19． 本小题主要考查空间线面关系和锥体体积的计算，考查逻辑思维能力、空间想象能力和运算能力。
解：(1)连结AC，则
，又AC是A1C在平面ABCD内的射影
∴
；
又∵
，且A1C在平面
内的射影
，
∴
，又∵
∴
……………… 3分
(2) 容易证明BF⊥平面A1B1C，
∴所求距离即为BF＝12/5 ……………… 6分
(3) 同上∵BF⊥平面A1B1C，，而BF在平面BDE上，
∴平面A1B1C⊥平面BDE……………… 8分
(4)连结DF，A1D，∵
，
，∴
，∴∠EDF即为ED与平面A1B1C所成的角 6分 由条件
，
，可知
，
，
，
，
·
，
·
∴
∴
∴ED与平面A1B1C所成角为arcsin
………………12分
20．本小题主要考查求运用所学知识解决实际问题的能力。
|
＝
……………2分
由题意知f(5)＝400, f(x)＝f(5)(1+
)＝400(1+) ……………… 6分
从而每平方米的综合费用为y=f(x)+＝20（x+
）+300≥20.2
+300＝620（元），当且仅当x=8时等号成立 ……………… 10分
故当建成8座球场时，每平方米的综合费用最省. ……………… 12分
21．本小题主要考查直线与圆锥曲线的有关知识，以及综合运用数学知识解决问题的能力。
解：（I）设线段AB的中点为
则
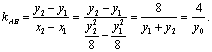
线段AB的垂直平分线的方程为
①…………………………3分
为方程①的一个解，
即以（6，0）为坐标的点在线段AB的垂直平分线上，
∴线段AB的垂直平分线过定点Q（6，0）．…………………………………………6分
（Ⅱ）由（I）知，直线AB的方程为
由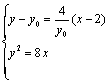
消去x，得
②
依题意y1、y2为方程②的两个实数根，且y1≠y2，
∴
解得－4＜y0＜4．……………………………………8分
又
Q（6，0）到直线AB的距离 
…………………………………10分
当且仅当
时取等号，
此时
故当A、B两点的距离为
时，△AQB的面积最大．…………………………12分
22. 本小题主要考查函数的性质等有关知识，以及综合运用数学知识解决问题的能力。
（1）证明：由 y=
f(x
)= ax2+bx+c
y= g(x) = ax+b
得ax2+(b－a)x+(c－b)=0 (*)
Δ=(b－a)2－4a (c－b)
∵f(x)=ax2+bx+c, f(1)=0
∴f(1)=a+b+c=0 ………………3分
又a＞b＞c
∴3a＞a+b+c＞3c即a＞0,c＜0
∴b－a＜0,c－b＜0,a＞0
∴Δ=(b－a)2－4a(c－b)＞0
故函数y=f(x)与y=g(x)的图象有两个交点；………………5分
（2）解：设A、B的坐标分别为（x1,y1）、（x2，y2），
则x1、x2是方程（*）的两根
故x1+x2=－
,
x1x2=
,所以｜A1B1｜=｜x1－x2｜=
=
=
又a+b+c=0,故b=－(a+c)
因而(b－a)2－4a(c－b)=(－2a－c)2－4a(a+2c)=c2－4ac
故｜A1B1｜=
=
=
……………… 8分
∵a＞b＞c,a+b+c=0
∴a＞－(a+c)＞c
∴－2＜
＜－
∴｜A1B1｜的取值范围是（
，2）……………… 10分.
(3)证明：不妨设x1＞x2,则由（2）知：
＜x1－x2＜2 ①
x1+x2=－=1－
由a＞b＞c得：＜＜1,
故0＜1－＜1－ ……………… 12分
又－2＜＜－,
故＜1－＜3,
因而0＜1－≤
即0＜x1－x2≤ ②
由①、②得：－＜x2≤0,
即方程（*），也就是方程f(x)－g(x)=0的较小根的范围是（－，0].
又a＞0,故当x≤－时，
f(x)－g(x)＞0恒成立，
即当x≤－时，恒有f(x)＞g(x) ……………… 14分.
附：（若觉18、20题有所不适合，可选以下2个备选题，立几题与两个20题皆为我改造的题目）
18题 备选题
已知数列
是由正数组成的等差数列，
是其前n项的和，并且
，
。
（I）求数列的通项公式；
（Ⅱ）证明：不等式
对一切n∈N均成立；
解：设数列的公差为d，由已知得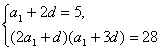
……2分
∴(5+d)(10-3d)=28，
∴
，
解之得d=2或
。
∵数列各项均正，∴d=2，∴
。
∴
。…………………… 5分
（Ⅱ）证明：∵n∈N，
∴只需证明
成立。…………………7分
（i）当n=1时，左=2，右=2，∴不等式成立。……………………8分
（ii）假设当n=k时不等式成立，即
。
那么当n=k+1时，
………………10分
以下只需证明
。
即只需证明
。…………11分
∵
。
∴
。
综合（i）（ii）知，不等式对于n∈N都成立。……………………12分
20题 备选题
某大型超市预计从明年初开始的前x个月内，某类服装的销售总量f（x）（千件）与月份数x的近似关系为
（Ⅰ）写出明年第x个月的需求量g（x）（千件）与月份数x的函数关系；
（Ⅱ）求出哪个月份的需求量超过1.4千件，并求出这个月的需求量．
解：（Ⅰ）第一个月销售量为
当
时，第x个月的销售量为
…………………………………………5分
当x=1时，g（1）也适合上式．
………………………………………………7分
（Ⅱ）由题意可得：
解之得
………………………………………………10分
………………………………………………………………………11分
答：第六个月销售量超过1.4千件，为1.44千件．………………………………12分
2004.2.12.