不等式与解析几何(一)
1、若![]() 则下列结论不正确的是 ( )
则下列结论不正确的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、使不等式![]() 成立的x的取值范围是 ( )
成立的x的取值范围是 ( )
A.(0,1) B.![]() C.
C.![]() D.
D.![]()
3、在双曲线![]() 上有一个点P,F1、F2为该双曲线的两个焦点,∠F1PF2=90°,
上有一个点P,F1、F2为该双曲线的两个焦点,∠F1PF2=90°,
且△F1PF2的三条边长成等差数列,则此双曲线的离心率是 ( )
A.2 B.3 C.4 D.5
4、已知函数![]() 均在(a,b)内可导,在[a,b]上连续,且
均在(a,b)内可导,在[a,b]上连续,且![]() ,
,
则在(a,b)上有 ( )
A.f(x)与g(x)大小关系不确定 B.f(x)<g(x) C.f(x)=g(x) D.f(x)>g(x)
5、若一个圆的圆心在抛物线![]() 的焦点处,且此圆与直线
的焦点处,且此圆与直线![]() 相切,则这个圆的方程是 ( )
相切,则这个圆的方程是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6、已知AB=4,M是AB的中点,点P在平面内运动且保持PA+PB=6,则PM的最大值和最小值分别是 ( )
A.3和![]() B.5和
B.5和![]() C.3和
C.3和![]() D.4和
D.4和![]()
7、过曲线![]() 上一点,倾斜角为
上一点,倾斜角为![]() 的切线方程为 ( )
的切线方程为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、若直线![]() 与线段AB有交点,其中A(-2,3),B(3,2),则
与线段AB有交点,其中A(-2,3),B(3,2),则![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9、把直线![]() 按向量
按向量![]() 平移后,所得直线与圆
平移后,所得直线与圆![]() 相
相
切,则实数![]() 的值为 ( )
的值为 ( )
A.39 B.13 C.-21 D.-39
10、设x、![]() 的最小值为 ( )
的最小值为 ( )
A.![]() B.
B.![]() C.-2 D.
C.-2 D.![]()
11、若![]() ,则
,则![]() 是
是![]() 成立的 ( )
成立的 ( )
A.必要非充分条件 B.充分非必要条件 C.充要条件 D.既不充分也不必要条件
12、已知直线![]() ( )
( )
A.![]() 的充要条件 B.
的充要条件 B.![]() 的必要不充分条件
的必要不充分条件
C.![]() 的充要条件 D.
的充要条件 D.![]() 的充分不必要条件
的充分不必要条件
13、若![]() 则 ( )
则 ( )
A.R<P<Q B.P<R<Q C.Q<P<R D.P<Q<R
14、设P(x,y)是曲线C:![]() 上任意一点,则
上任意一点,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
15、若点P(x,y)在曲线![]() (θ为参数)上,则使x2+y2取最大值的点P的坐标是
( )
(θ为参数)上,则使x2+y2取最大值的点P的坐标是
( )
A.(6,-8) B.(-6,8) C.(3,-4) D.(-3,4)
16、已知点![]() (
(![]() )是圆
)是圆![]() :
:![]() 内一点,直线
内一点,直线![]() 是以
是以![]() 为中点的弦所在的直线,直线
为中点的弦所在的直线,直线![]() 的方程是
的方程是![]() ,那么 ( )
,那么 ( )
A.![]() ∥
∥![]() 且
且![]() 与圆
与圆![]() 相离
B.
相离
B.![]()
![]()
![]() 且
且![]() 与圆
与圆![]() 相离
相离
C.![]() ∥
∥![]() 且
且![]() 与圆
与圆![]() 相切 D.
相切 D.![]()
![]()
![]() 且
且![]() 与圆
与圆![]() 相切
相切
17、直线![]() 、
、![]() 分别过点P(-1,3),Q(2,-1),它们分别绕P、Q旋转,但始终保持平行,则
分别过点P(-1,3),Q(2,-1),它们分别绕P、Q旋转,但始终保持平行,则![]() 、
、![]() 之间的距离
之间的距离![]() 的取值范围为 ( )
的取值范围为 ( )
A.![]() B.(0,5) C.
B.(0,5) C.![]() D.
D.![]()
18、在圆![]() 有n条弦的长度成等差数列,最小弦长为数列的首项
有n条弦的长度成等差数列,最小弦长为数列的首项
![]() ,最大弦长为
,最大弦长为![]() ,若公差
,若公差![]() ,那么n的取值集合为 ( )
,那么n的取值集合为 ( )
A.{3,4,5} B.{4,5,6} C.{3,4,5,6} D.{4,5,6,7}
19、若圆锥曲线![]() 的焦距与
的焦距与![]() 无关,则它的焦点坐标是
.
无关,则它的焦点坐标是
.
20、函数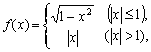 如果方程
如果方程![]() 有且只有一个实根,那么
有且只有一个实根,那么![]() .
.
21、圆心在抛物线y2=2x上,且与x轴和该抛物线的准线都相切的一个圆的方程是__________.
22、设S为平面内以A(4,1),B(-1,6),C(-3,2)为顶点的三角形区域(包含边界),P(x,y)为S内一点,则t=4x-3y的最小值为 .
23、若a,b,a+b成等差数列,a,b,ab成等比数列,且![]() ,则
,则![]() 的取值范
的取值范
围是 ____________ .
24、椭圆![]() 上一点P的横坐标为2,P到两焦点的距离分别为6.5和3.5,则
上一点P的横坐标为2,P到两焦点的距离分别为6.5和3.5,则![]() ,
,![]() = .
= .
25、若z=![]() 满足约束条件
满足约束条件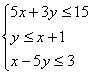 ,则Z的最大值和最小值分别为____
,则Z的最大值和最小值分别为____
不等式与解析几何(二)
1、M(![]() 为圆
为圆![]() 内异于圆心的一点,则直线
内异于圆心的一点,则直线![]() 与该圆
与该圆
的位置关系为 ( )
A.相切 B.相交 C.相离 D.相切或相交
2、设动点P在直线![]() 上,O为坐标原点.以OP为直角边、点O为直角顶点作等腰
上,O为坐标原点.以OP为直角边、点O为直角顶点作等腰![]() ,则动点Q的轨迹是
( )
,则动点Q的轨迹是
( )
A.圆 B.两条平行直线 C.抛物线 D.双曲线
3、已知P是椭圆![]() 第三象限内一点,且它与两焦点连线互相垂直,若点P到直线
第三象限内一点,且它与两焦点连线互相垂直,若点P到直线![]() 的距离不大于3,则实数m的取值范围是
( )
的距离不大于3,则实数m的取值范围是
( )
A. [-7,8] B.![]() C. [-2,2] D.
C. [-2,2] D.![]()
 4、已知椭圆
4、已知椭圆![]() 的右焦点为F,Q、P分别为椭圆上和椭圆外一点,且点Q
的右焦点为F,Q、P分别为椭圆上和椭圆外一点,且点Q
为FP的中点,则点P的轨迹方程为 ( )
A.![]() B.
B. ![]()
C.![]() D.
D. ![]()
5、如图,过抛物线![]() 的焦点F的直线
的焦点F的直线![]() 交抛物线于点A、B,交其准线于点C,若
交抛物线于点A、B,交其准线于点C,若![]() ,且
,且![]() ,则此抛物线的方程为
( )
,则此抛物线的方程为
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6、已知6枝玫瑰与3枝康乃馨的价格之和大于24元,而4枝玫瑰与5枝康乃馨的价格之和小于22元,则2枝玫瑰的价格和3枝康乃馨的价格比较结果是 ( )
A.2枝玫瑰价格高 B.3枝康乃馨价格高 C.价格相同 D.不确定
7、若不等式![]() ,则实数a的取值集合为 ( )
,则实数a的取值集合为 ( )
A. {![]() } B. {1} C.
} B. {1} C. ![]() D. {
D. {![]() }
}
8、用清水投洗衣服,若每次能洗去污垢的![]() ,要使存留的污垢不超过1%,则至少要投洗的次数是
( )
,要使存留的污垢不超过1%,则至少要投洗的次数是
( )
A.3 B.4 C.5 D.6
9、设双曲线![]() (b>a>0)的半焦距为c,直线l过(a, 0)、(0, b)两点,已知原点到直线l的距离是
(b>a>0)的半焦距为c,直线l过(a, 0)、(0, b)两点,已知原点到直线l的距离是![]() c,则双曲线的离心率是( )
c,则双曲线的离心率是( )
(A)2 (B)![]() (C)
(C)![]() (D)
(D)![]()
10、若![]() 则使
则使![]() 成立的充分不必要条件是_______
成立的充分不必要条件是_______
A ![]() B
B ![]() C
C ![]() D
D ![]()
11、若不等式![]() 对于任意实数
对于任意实数![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是_______
的取值范围是_______
A ![]() B
B ![]() C
C ![]() D
D ![]()
12、已知实数![]() 满足条件
满足条件![]() 则
则![]()
![]() 的取值范围是_____
的取值范围是_____
A ![]() B
B ![]() C
C ![]() D
D ![]()
13、若![]() 则_____
则_____
A ![]() B
B ![]() C
C ![]() D
D ![]()
14、一个直角三角形的周长为![]() 其斜边长的最小值为______
其斜边长的最小值为______
A ![]() B
B ![]() C
C ![]() D
D ![]()
15、若![]() 且
且![]() 设
设![]() 则____
则____
A ![]() B
B ![]() C
C ![]() D
D ![]()
16、设P为椭圆![]() 上的点,F1、F2为椭圆的焦点,∠F1PF2=
上的点,F1、F2为椭圆的焦点,∠F1PF2=![]() ,则△PF1F2的面积等于( ) (A)
,则△PF1F2的面积等于( ) (A)![]() (B)
(B)![]() ) (C)
) (C)![]() ) (D)16翰林汇
) (D)16翰林汇
17、若AB为抛物线y2=2px
(p>0)的动弦,且AB=a
(a>p),则AB的中点M到y轴的最近距离是( ) (A)![]() a (B)
a (B)![]() p (C)
p (C)![]() a+
a+![]() p (D)
p (D)![]() a-
a-![]() p
p
18、已知平面内有一固定线段AB,其长度为4,动点P满足PA-PB=3,则PA的最小值为( )
(A)1.5 (B)3 (C)0.5 (D)3.5
19、已知椭圆![]() 的左、右顶点分别为A、B,如果椭圆上存在点Q使得∠AQB=120°,则椭圆的离心率的取值范围为_________
的左、右顶点分别为A、B,如果椭圆上存在点Q使得∠AQB=120°,则椭圆的离心率的取值范围为_________
20、若方程![]() 表示两条直线,则其系数
表示两条直线,则其系数![]() 满足的条件为_____
满足的条件为_____
21、已知函数![]() 的图象与函数
的图象与函数![]() 的图象有两个交点
的图象有两个交点![]() 则
则![]() =______
=______
22、函数![]() 的一条对称轴方程是
的一条对称轴方程是![]() ,则直线
,则直线![]() 的倾斜角为_______
的倾斜角为_______
23、若双曲线![]() 的一条准线恰好是圆
的一条准线恰好是圆![]() 的一条切线,则实数
的一条切线,则实数![]() _
_
24、设三角形ABC的BC边上的高AD=BC,![]() 分别为其对应边,则
分别为其对应边,则![]() 的最大值为25、设F1和F2是双曲线
的最大值为25、设F1和F2是双曲线 ![]() -y2=1 的两个焦点,点P在双曲线上,且满足∠F1PF2=90°,则△F1PF2的面积是( )。
-y2=1 的两个焦点,点P在双曲线上,且满足∠F1PF2=90°,则△F1PF2的面积是( )。
(A)1 (B)![]() (C)2
(D)
(C)2
(D)![]()
26、已知![]() 分别为圆锥曲线
分别为圆锥曲线![]() 和
和![]() 的离心率,则
的离心率,则
![]() 的值( )
的值( )
A 一定是正数 B 一定是零 C 一定是负数 D 以上答案均不对
27、如果直线L沿x轴负方向平移3个单位,再沿y轴正方向平移1个单位后,又回到原来的位置,那么直线L的斜率是( )
(A)-![]() (B)-3
(C)
(B)-3
(C) ![]() (D)3
(D)3
28、圆C:x2+y2+2x+4y-3=0上到直线x+y+1=0的距离为![]() 的点有( )
的点有( )
(A) 1个 (B)2个 (C)3个 (D)4个
29、设F1、F2是椭圆![]() 的两个焦点,P是椭圆上不与长轴两个端点重合的一点,则(
)
(A)△PF1F2的面积是定值
(B)∠F1PF2是定角
的两个焦点,P是椭圆上不与长轴两个端点重合的一点,则(
)
(A)△PF1F2的面积是定值
(B)∠F1PF2是定角
(C)△PF1F2的周长是定值 (D)△PF1F2中边F1F2的中线长为定值翰林汇
30、若直线![]() 始终平分圆
始终平分圆![]() 的周长,则
的周长,则![]() 的取值范围是( )
的取值范围是( )
A (0,1) B
(0,![]() C
C ![]() D
D ![]()
31、已知两圆![]() ,动圆M与两圆C1、C2都相切,则动圆圆心M的轨迹方程是_________
,动圆M与两圆C1、C2都相切,则动圆圆心M的轨迹方程是_________
32、已知曲线![]() 则在曲线上
点处的切线与直线
则在曲线上
点处的切线与直线![]() 垂直.
垂直.
33、已知两定圆![]() =12,求经过一定圆圆心且与另一定圆内切的圆的圆心轨迹C的方程;
=12,求经过一定圆圆心且与另一定圆内切的圆的圆心轨迹C的方程;
高考不等式与解析几何专题复习
1、已知椭圆E的离心率为e,两焦点为F1、F2,抛物线C以F1为顶点,F2为焦点,P为两曲线的一个交点。若![]() ,则
,则![]() 的值为( )
的值为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
2、已知函数![]() 在
在![]() 上是减函数,又
上是减函数,又![]() 是偶函数,若
是偶函数,若![]()
![]() ,则
,则![]() 从小到大的顺序是____
从小到大的顺序是____
3、直线![]() 与
与![]() 轴、
轴、![]() 轴的正半轴所围成的四边形有外接圆,则
轴的正半轴所围成的四边形有外接圆,则![]() 的值是( ) A -1 B -
的值是( ) A -1 B -![]() C
C ![]() D 2
D 2
4、已知动点P![]() 满足
满足![]() ,则P点的轨迹是( )
,则P点的轨迹是( )
A 椭圆 B 双曲线 C 抛物线 D 两相交直线
5、已知点![]() 及抛物线
及抛物线![]() 上一动点P(x,y),则y+PQ的最小值是 ( )
上一动点P(x,y),则y+PQ的最小值是 ( )
A.2 B.3 C.4 D.![]()
6、已知点F为双曲线![]() 的右焦点,M为双曲线右支上一动点,定点A的坐标是(5,4),则
的右焦点,M为双曲线右支上一动点,定点A的坐标是(5,4),则![]() 的最大值为____
的最大值为____
7、椭圆![]() 的左焦点为F,A
的左焦点为F,A![]() 是两个顶点,如果点F到直线AB的距离等于
是两个顶点,如果点F到直线AB的距离等于![]() 那么该椭圆的离心率等于_____
那么该椭圆的离心率等于_____
8、![]() 满足
满足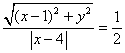 ,则
,则![]()
9、![]() 求证:
求证:![]()
10、某种车辆,购车费10万元,每年交保险费、养路费及汽油费合计9千元,汽车的维修费平均为:第一年2千元,第二年4千元,第三年6千元,依等差数列逐年递增,问使用多少年平均费用最少?
11、试问: 是否存在常数![]() ,使得不等式
,使得不等式![]()
对任意的正数![]() 均成立,请证明你的结论.
均成立,请证明你的结论.
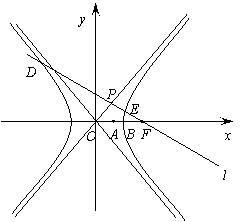
12、已知双曲线![]() :
:![]()
![]() ,
, ![]() 是右顶点,
是右顶点,![]() 是右焦点, 点
是右焦点, 点![]() 在
在![]() 轴正半轴上,且满足
轴正半轴上,且满足![]() 成等比数列,过
成等比数列,过![]() 作双曲线
作双曲线![]() 在第一、三象限的渐近线的垂线
在第一、三象限的渐近线的垂线![]() ,垂足为
,垂足为![]() .
.
(Ⅰ)求证:![]() ;(Ⅱ)若
;(Ⅱ)若![]() 与双曲线
与双曲线![]() 的左、右两支分别相交 于点
的左、右两支分别相交 于点![]() 、
、![]() ,求双曲线
,求双曲线![]() 的离心率
的离心率![]() 的取值范围.
的取值范围.
13、已知动点![]() 与双曲线
与双曲线![]() 的两个焦点
的两个焦点![]() 、
、![]() 的距离之和为定值,且
的距离之和为定值,且![]()
![]() 的最小值为
的最小值为![]() .(I)求动点
.(I)求动点![]() 的轨迹方程; (II)若已知
的轨迹方程; (II)若已知![]() ,
,![]() 、
、![]() 在动点
在动点![]() 的轨迹上且
的轨迹上且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
14、椭圆![]() 的左、右焦点分别为F1、F2,右顶点为A,M为椭圆C1上任意一点,且
的左、右焦点分别为F1、F2,右顶点为A,M为椭圆C1上任意一点,且![]() 的最小值为
的最小值为![]() .(1)求椭圆C1的离心率;(2)设双曲线C2以椭圆C1的焦点为顶点,顶点为焦点;在第一象限内任取双曲线C2上一点P,试问是否存在常数
.(1)求椭圆C1的离心率;(2)设双曲线C2以椭圆C1的焦点为顶点,顶点为焦点;在第一象限内任取双曲线C2上一点P,试问是否存在常数![]() ,使得
,使得![]() 恒成立?证明你的结论.
恒成立?证明你的结论.
15、某集团准备兴办一所中学,投资1200万用于硬件建设.为了考虑社会效益和经济利益,对该地区教育市场进行调查,得出一组数据列表(以班为单位)如下:
| 班级学生数 | 配备教师数 | 硬件建设(万元) | 教师年薪(万元/人) | |
| 初中 | 60 | 2.0 | 28 | 1.2 |
| 高中 | 40 | 2.5 | 58 | 1.6 |
根据有关规定,除书本费、办公费外,初中生每年可收取学费600元,高中生每年可收取学费1500元.因生源和环境等条件限制,办学规模以20至30个班为宜.根据以上情况,请你合理规划办学规模使年利润最大,最大利润多少万元?(利润=学费收入-年薪支出)
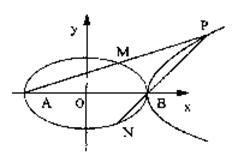
16、椭圆C1:![]() =1(a>b>0)的左右顶点分别为A、B.点P双曲线C2:
=1(a>b>0)的左右顶点分别为A、B.点P双曲线C2:![]() =1在第一象限内的图象上一点,直线AP、BP与椭圆C1分别交于C、D点.若△ACD与△PCD的面积相等.(1)求P点的坐标;(2)能否使直线CD过椭圆C1的右焦点,若能,求出此时双曲线C2的离心率,若不能,请说明理由.
=1在第一象限内的图象上一点,直线AP、BP与椭圆C1分别交于C、D点.若△ACD与△PCD的面积相等.(1)求P点的坐标;(2)能否使直线CD过椭圆C1的右焦点,若能,求出此时双曲线C2的离心率,若不能,请说明理由.
17、
|
18、已知椭圆![]() 的一条准线方程是
的一条准线方程是![]() 其左、右顶点分别是A、B;双曲线
其左、右顶点分别是A、B;双曲线![]() 的一条渐近线方程为3x-5y=0.
的一条渐近线方程为3x-5y=0.
(Ⅰ)求椭圆C1的方程及双曲线C2的离心率;
(Ⅱ)在第一象限内取双曲线C2上一点P,连结AP交椭圆C1于点M,连结PB并延长交椭圆C1于点N,若![]() . 求证:
. 求证:![]()
19、解关于x的不等式![]()
20、已知函数![]()
(1)设![]() 处取得极值,其中
处取得极值,其中![]() 求证:
求证:![]() ;
;
(2)设点A(![]() ,求证:线段AB的中点C在曲线
,求证:线段AB的中点C在曲线![]()
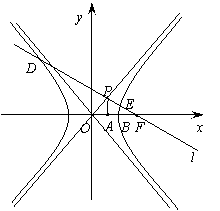 12、(Ⅰ)法一:
12、(Ⅰ)法一: ![]() ,
,
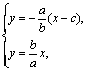 解得
解得![]()

| |
| |
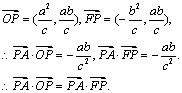
| |
| |
| |
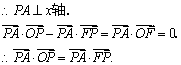 (Ⅱ)
(Ⅱ)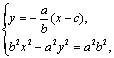
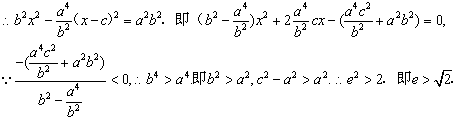
11、当![]() 时,有
时,有![]() ,此时有不等式
,此时有不等式![]() (*)先证左不等式,去分母有理化
(*)先证左不等式,去分母有理化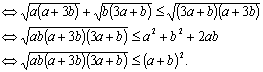
![]()
![]()
![]() 得证. 再证右不等式,去分母有理化
得证. 再证右不等式,去分母有理化 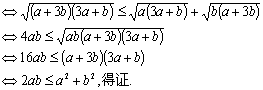
![]()
综合以上可知,不等式(*)获证. 故存在常数![]() 满足题意.
满足题意.
13、(I)由题意![]() ,设
,设![]() (
(![]() ),由余弦定理, 得
),由余弦定理, 得
![]() .
.
又![]() ·
·![]() ,当且仅当
,当且仅当![]() 时,
时,![]() ·
·![]() 取最大值,
取最大值,
此时![]() 取最小值
取最小值![]() ,令
,令![]() ,解得
,解得![]() ,
,![]() ,∴
,∴![]() ,故所求
,故所求![]() 的轨迹方程为
的轨迹方程为![]() .
.
(II)设![]() ,
,![]() ,则由
,则由![]() ,可得
,可得![]() ,
,
故![]() ,∵
,∵![]() 、
、![]() 在动点
在动点![]() 的轨迹上,故
的轨迹上,故![]() 且
且![]() ,消去
,消去![]() 可得
可得![]() ,解得
,解得![]() ,
,
又![]() ,∴
,∴![]() ,解得
,解得![]() ,故实数
,故实数![]() 的取值范围是
的取值范围是![]() .
.
14、(1)解:作出椭圆的左准线l,作MN⊥l交l于点N.
|
根据椭圆的定义得:![]() ,所以
,所以
![]() ,同理可得:
,同理可得:
![]() 所以
所以![]()
由MF1·MF2的最小值为![]() 得:
得:
|
[注:若学生没有证明MF1=![]()
而直接使用此结论,则(Ⅰ)中扣去1分]
(Ⅱ)解:依题意得双曲线C2的离心率为2,
设C2的方程是![]() 假设存在适合题意的常
假设存在适合题意的常
数![]() ,①先来考查特殊情形下的
,①先来考查特殊情形下的![]() 值:
值:
PA⊥x轴时,将x=2c代入双曲线方程,解得y=3c,
因为AF1=3c,所以△PAF1是等腰直角三角形,
∠PAF1=90°,∠PF1A=45°,此时![]() =2………7分
=2………7分
②以下证明当PA与x轴不垂直时,∠PAF1=2∠PF1A恒成立.
设![]() ,由于点P在第一象限内,所以直线PF1斜率存在,
,由于点P在第一象限内,所以直线PF1斜率存在,![]() ;
;
因为PA与x轴不垂直,所以直线PA斜率也存在,![]() .
.
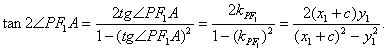 因为
因为![]() 所以
所以![]() ,将其代入上式并化简得:
,将其代入上式并化简得:
![]() 因为∠PAF1+∠PAx=180°,
因为∠PAF1+∠PAx=180°,
所以![]() 即tan2∠PF1A=tg∠PAF1.………………12分
即tan2∠PF1A=tg∠PAF1.………………12分
因为∠![]() ∠
∠![]() 所以∠PAF1、
所以∠PAF1、
2∠PF1A![]() 所以∠PAF1=2∠PF1A恒成立.
所以∠PAF1=2∠PF1A恒成立.
综合①、②得:存在常数![]() ,使得对位于双曲线C2在第一象限内的任意一点p,
,使得对位于双曲线C2在第一象限内的任意一点p,
∠PAF1=2∠PF1A恒成立.……………………14分
[注:②中如果学生认为∠PAF1、2∠PF1A![]() 本题不扣分]
本题不扣分]
15、解:设初中x个班,高中y 个班,则![]() ……………(4分)
……………(4分)
设年利润为s,则![]() ……(6分)
……(6分)
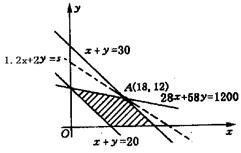
作出(1)、(2)表示的平面区域,如图,易知当直线1.2x+2y=s过点A时,s有最大值.
|
![]() (万元).
(万元).
即学校可规划初中18个班,高中12个班,
可获最大年利润为45.6万元.……(12分)
16、解:(1)设P(x0,y0)(x0>a,y0>0),又有点
A(-a,0),B(a,0).

![]() …………………………(7分)
…………………………(7分)
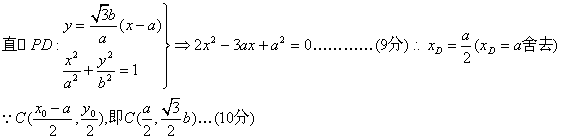
∴CD垂直于x轴.若CD过椭圆C1的右焦点,则
![]()
故可使CD过椭圆C1的右焦点,此时C2的离心率为![]() .…………(12分)
.…………(12分)
17、解:由题意,![]() ∴
∴![]() 椭圆方程可设为:
椭圆方程可设为:
![]() 设直线l:y=k(x-1),显然k≠0,将直线方程代入椭圆方程:
设直线l:y=k(x-1),显然k≠0,将直线方程代入椭圆方程:
![]() 整理得:
整理得:
![]() ①设交点A(
①设交点A(![]() ),B(
),B(![]() ),中点M(
),中点M(![]() ),而中点在直线
),而中点在直线![]() 上, ∴
上, ∴![]()
∴![]() ,求得:k=-1,将k=-1代入①,
,求得:k=-1,将k=-1代入①,![]()
其中△>0求得![]() ,点F(c,0)关于直线l:y=-x+1的对称点(1,1-c)在椭圆上,代入椭圆方程:∴1+2(1-c)2-2c2=0, ∴c=
,点F(c,0)关于直线l:y=-x+1的对称点(1,1-c)在椭圆上,代入椭圆方程:∴1+2(1-c)2-2c2=0, ∴c=![]() ∴所求椭圆为C:
∴所求椭圆为C:
![]() ,直线l方程为:
,直线l方程为:![]()
20、解(1)![]() ,据题意知s,t为二次方程
,据题意知s,t为二次方程![]() 的两根…2分,
的两根…2分,
![]()
![]()
![]() …6分
…6分![]()
![]() …7分
…7分
(2)![]() …9分
…9分
![]()
![]()
(12分)又![]()
故AB中点![]() ………………………………14分
………………………………14分