高考第一轮总复习同步试卷(十一)
集合、函数、数列
一、选择题(5×12=60)
(1)(2000天津)设集合A和B都是坐标平面上的点集![]() ,映射
,映射![]() 把集合A中的元素
把集合A中的元素![]() 映射成集合B中的元素
映射成集合B中的元素![]() ,则在映射
,则在映射![]() 下,象
下,象![]() 的原象是( )
的原象是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(2)(2004云南)已知集合![]() ,
,![]() ,则集合
,则集合![]() =( )
=( )
A.{![]() }
B.{
}
B.{![]() } C.{
} C.{![]() }
D. {
}
D. {![]() }
}
(3)(2000天津)函数![]() 的部分图象是( )
的部分图象是( )
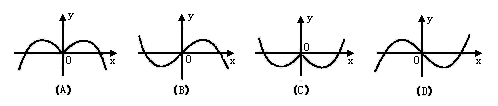
(4)(2001天津)若定义在区间(-1,0)内的函数![]() 的取值范围是(
)
的取值范围是(
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(5)(2002天津)设集合![]() 则( )
则( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(6)(2002天津)函数![]() 是单调函数的充要条件是( )
是单调函数的充要条件是( )
(A)b≥0 (B)b≤0 (C)b>0 (D)b<0
(7)(2002天津)已知![]() ,则有( )
,则有( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(8)(2003天津)函数![]() 的反函数为( )
的反函数为( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(9)(2003天津)已知方程![]() 的四个根组成一个首项为
的四个根组成一个首项为![]() 的等差数列,则
的等差数列,则![]() ( )
( )
(A)1
(B)![]() (C)
(C)![]() (D)
(D)![]()
(10)(2004天津)若函数![]() 在区间
在区间![]() 上的最大值是最小值的3倍,则a=(
)
上的最大值是最小值的3倍,则a=(
)
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
(11)(2004天津)函数![]() (
(![]() )的反函数是( )
)的反函数是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
(12)(2004云南)函数![]() 的图象( )
的图象( )
A.与![]() 的图象关于y轴对称 B.与
的图象关于y轴对称 B.与![]() 的图象关于坐标原点对称
的图象关于坐标原点对称
C.与![]() 的图象关于
的图象关于![]() 轴对称 D.与
轴对称 D.与![]() 的图象关于坐标原点对称
的图象关于坐标原点对称
高考第一轮总复习同步试卷(十一)
集合、函数、数列
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题(4×4=16)
(13)(2000天津)设![]() 是首项为1的正项数列,且
是首项为1的正项数列,且![]() (
(![]() =1,2,3,…),则它的通项公式是
=1,2,3,…),则它的通项公式是![]() =
。
=
。
(14)(2001天津)设{an}是公比为q的等比数列,Sn是它的前n项和,若{Sn}是等差数列,则q = .
(15)(2002天津)函数![]() 图象与其反函数图象的交点坐标为_ __。
图象与其反函数图象的交点坐标为_ __。
(16)(2002天津)已知函数![]() ,那么
,那么![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+ ![]() =
。
=
。
三、解答题(17-21题每题12分,22题14分)
(17)(2004云南)(本小题满分12分)
数列![]() 的前n项和记为Sn,已知
的前n项和记为Sn,已知![]() 证明:
证明:
(Ⅰ)数列![]() 是等比数列;
是等比数列;
(Ⅱ)![]()
(18)(2001天津)(本小题满分12分)
设![]() 是R上的偶函数.
是R上的偶函数.
(Ⅰ)求a的值;
(Ⅱ)证明f(x)在(0,+∞)上是增函数.
(19)(2000天津)(本小题满分12分)
设函数![]() ,其中
,其中![]() 。
。
(I)解不等式![]() ;
;
(II)求![]() 的取值范围,使函数
的取值范围,使函数![]() 在区间
在区间![]() 上是单调函数。
上是单调函数。
(20)(2004上海)(本题满分12分)
记函数f(x)=![]() 的定义域为A, g(x)=lg[(x-a-1)(2a-x)](a<1)
的定义域为B.
的定义域为A, g(x)=lg[(x-a-1)(2a-x)](a<1)
的定义域为B.
(1) 求A;
(2) 若B![]() A, 求实数a的取值范围.
A, 求实数a的取值范围.
(21)(2002天津)(本题满分12分)已知![]() 是由非负整数组成的数列,满足
是由非负整数组成的数列,满足![]() ,
,![]() ,
,![]() =
=![]() ,
,![]() ……。
……。
(1)求![]() ;
;
(2)证明![]() ……;
……;
(3)求![]() 的通项公式及其前
的通项公式及其前![]() 项和
项和![]() 。
。
(22)(2003天津)(本小题满分14分)
设![]() 为常数,且
为常数,且![]() .
.
(Ⅰ)证明对任意![]() ≥1,
≥1,![]() ;
;
(Ⅱ)假设对任意![]() ≥1有
≥1有![]() ,求
,求![]() 的取值范围.
的取值范围.
(附加题)(2004天津)(本小题满分15分)
已知定义在R上的函数![]() 和数列
和数列![]() 满足下列条件:
满足下列条件:![]() ,
,![]() (n=2,3,4,…),
(n=2,3,4,…),![]() ,
,![]() -
-![]() =
=![]() (n=2,3,4,…),其中a为常数,k为非零常数。
(n=2,3,4,…),其中a为常数,k为非零常数。
(1)令![]()
![]() ,证明数列
,证明数列![]() 是等比数列;
是等比数列;
(2)求数列![]() 的通项公式;
的通项公式;
(3)当![]() 时,求
时,求![]() 。
。
高考第一轮总复习同步试卷(十一)
集合、函数、数列
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | C | D | A | B | A | D | B | C | A | D | D |
13、![]() 14、1
15、(0,0)、(1,1) 16、
14、1
15、(0,0)、(1,1) 16、![]()
(17)本小题主要考查数列、等比数列的概念和性质,分析和推理能力,满分12分。
证明:(Ⅰ)∵![]()
∴ ![]() 整理得
整理得 ![]()
所以 ![]() 故
故![]() 是以2为公比 的等比数列.
是以2为公比 的等比数列.
(Ⅱ)由(Ⅰ)知![]() 于是
于是 ![]()
又 ![]() 故
故 ![]()
因此对于任意正整数 ![]() 都有
都有![]()
(18)本小题主要考查函数的奇偶性和单调性等基本性质,指数函数和不等式的基本性质和运算,以及综合分析问题的能力.
(I)解:依题意,对一切![]() 有
有![]() ,即
,即![]()
所以![]() 对一切
对一切![]() 成立.
成立.
由此得到![]() 即a2=1.
即a2=1.
又因为a>0,所以a=1.
(II)证明一:设0<x1<x2,
![]()
![]()
由![]()
![]()
![]() 即f(x)在(0,+∞)上是增函数.
即f(x)在(0,+∞)上是增函数.
证明二:由![]() 得
得![]()
当![]() 时,有
时,有![]() 此时
此时![]()
所以f(x)在(0,+∞)上是增函数.
(19)本小题主要考查不等式的解法、函数的单调性等基本知识、分类讨论的数学思想方法和运算、推理能力。满分12分。
解:(I)不等式![]() 即
即![]() ,
,
由此可得![]() ,即
,即![]() ,其中常数
,其中常数![]() 。所以,原不等式等价于
。所以,原不等式等价于
![]() 即
即![]() ——3分
——3分
所以,当![]() 时,所给不等式的解集为
时,所给不等式的解集为![]() ;
;
当![]() 时,所给不等式的解集为
时,所给不等式的解集为![]() 。——6分
。——6分
(II)在区间![]() 上任取
上任取![]() ,
,![]() ,使得
,使得![]() <
<![]() 。
。
![]()
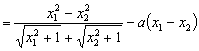
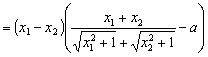 。——8分
。——8分
(i) 当![]() 时,
时,
∵ ![]() ,∴
,∴ ![]() ,
,
又![]() ,∴
,∴![]() ,即
,即![]() 。
。
所以,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是单调递减函数。 ——10分
上是单调递减函数。 ——10分
(ii)当![]() 时,在区间
时,在区间![]() 上存在两点
上存在两点![]() ,
,![]() ,满足
,满足 ![]() ,
,![]() ,即
,即![]()
![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上不是单调函数。
上不是单调函数。
综上,当且仅当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是单调函数。——12分
上是单调函数。——12分
(20)【解】(1)2-![]() ≥0, 得
≥0, 得![]() ≥0, x<-1或x≥1
≥0, x<-1或x≥1
即A=(-∞,-1)∪[1,+ ∞]
(2) 由(x-a-1)(2a-x)>0, 得(x-a-1)(x-2a)<0.
∵a<1,∴a+1>2a, ∴B=(2a,a+1).
∵B![]() A, ∴2a≥1或a+1≤-1, 即a≥
A, ∴2a≥1或a+1≤-1, 即a≥![]() 或a≤-2, 而a<1,
或a≤-2, 而a<1,
∴![]() ≤a<1或a≤-2, 故当B
≤a<1或a≤-2, 故当B![]() A时, 实数a的取值范围是(-∞,-2]∪[
A时, 实数a的取值范围是(-∞,-2]∪[![]() ,1)
,1)
(21)本小题主要考查数列与等差数列前n项和等基础知识,以及准确表述,分析和解决问题的能力。满分14分。
解:(1)由题设得![]() ,且
,且![]() 均为非负整数,所以
均为非负整数,所以![]() 的可能的值为1、2、5、10.
的可能的值为1、2、5、10.
若![]() =1,则
=1,则![]() =10,
=10,![]() =
=![]() ,与题设矛盾。
,与题设矛盾。
若![]() =5,则
=5,则![]() =2,
=2, ![]() ,与题设矛盾。
,与题设矛盾。
若![]() =10,则
=10,则![]() =1,
=1, ![]() ,
,![]() ,与题设矛盾。
,与题设矛盾。
所以![]() =2.
=2.
(2)用数学归纳法证明:
①当![]() ,等式成立。
,等式成立。
②假设当![]() 时等式成立,即
时等式成立,即![]() ,
,
由题设![]()
因为![]()
所以![]()
也就是说,当![]() 时,等式
时,等式![]() 成立。
成立。
根据①②,对于所有![]() 。
。
(3)由![]() 得
得
![]() ……。
……。
即![]() ……。
……。
所以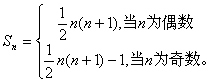
(22)本小题主要考查数列、等比数列的概念,考查数学归纳法,考查灵活运用数学知识分析问题和解决问题的能力,满分14分.
(1)证法一:(i)当n=1时,由已知a1=1-2a0,等式成立;
(ii)假设当n=k(k≥1)等式成立,则![]()
那么![]()
![]()
也就是说,当n=k+1时,等式也成立. 根据(i)和(ii),可知等式对任何n∈N,成立.
证法二:如果设![]() 用
用![]() 代入,可解出
代入,可解出![]() .
.
所以![]() 是公比为-2,首项为
是公比为-2,首项为![]() 的等比数列.
的等比数列.
![]() 即
即![]()
(2)解法一:由![]() 通项公式
通项公式 ![]()
![]() 等价于
等价于 ![]() ……①
……①
(i)当n=2k-1,k=1,2,…时,①式即为 ![]()
即为 ![]() ……②
……②
②式对k=1,2,…都成立,有 ![]()
(ii)当n=2k,k=1,2,…时,①式即为 ![]()
即为 ![]() ……③
③式对k=1,2,…都成立,有
……③
③式对k=1,2,…都成立,有
![]() 综上,①式对任意n∈N*,成立,有
综上,①式对任意n∈N*,成立,有![]()
故a0的取值范围为![]()
解法二:如果![]() (n∈N*)成立,特别取n=1,2有
(n∈N*)成立,特别取n=1,2有 ![]()
![]() 因此
因此 ![]() 下面证明当
下面证明当![]() 时,对任意n∈N*,
时,对任意n∈N*,
![]() 由an的通项公式
由an的通项公式 ![]()
(i)当n=2k-1,k=1,2…时,
![]()
![]()
![]()
(ii)当n=2k,k=1,2…时,
![]()
![]()
![]()
故a0的取值范围为![]()
(附加题)本小题主要考查函数、数列、等比数列和极限等概念,考查灵活应用数学知识分析问题和解决问题的能力,满分12分。
(1)证明:由![]() ,可得
,可得
![]() 。
。
由数学归纳法可证![]()
![]() 。
。
由题设条件,当![]() 时
时
![]()
![]()
![]()
因此,数列![]() 是一个公比为k的等比数列。
是一个公比为k的等比数列。
(2)解:由(1)知,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
![]() 。
。
而![]()
![]()
所以,当![]() 时
时
![]()
![]() 。
。
上式对![]() 也成立。所以,数列
也成立。所以,数列![]() 的通项公式为
的通项公式为
![]()
当![]() 时
时
![]()
![]() 。
。
上式对![]() 也成立,所以,数列
也成立,所以,数列![]() 的通项公式为
的通项公式为
![]()
![]() ,
,
(3)解:当![]() 时
时
![]()
![]()