第三节平面向量的数量积及运算律
【例1】判断下列各命题的真假，并说明理由。
（1）在△ABC中，若
，则△ABC是锐角三角形；
（2）在△ABC中，若
，则△ABC是钝角三角形；
（3）△ABC为直角三角形的充要条件是
；
（4）△ABC为斜角三角形的必要不充分条件是
【例2】已知a，b均为非零向量，且a+3b与
【例3】已知a=6，b=4，a，b夹角为60°，求a + b、a -3b
【例4】已知a + b + c=0，且a=3，b=5，c=7，求a与b的夹角。
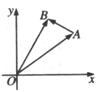【例5】如图，以
和
为两个顶点作等腰直角三角形
OAB，∠B=90°，求点B的坐标。
【例6】已知平面向量a=
，b=
（1）证明：a ⊥ b；
（2）若存在不同时为零的实数
和
，使x=a+(t 2 - 3)b，y =-ka +
tb，且x ⊥ y，试求函数关系式
；
（3）据（2）的结论，确定函数的单调区间。
【例7】设平面内两个向量a=
，b=
，且
（1）证明：(a + b) ⊥ (a - b)；
（2）若两个向量ka + b与a - kb的模相等，求
的值
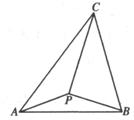【例8】如图所示，在△ABC内求一点P使
最小。
双基训练
1、若a、b、c为任意向量，
，则下列不等式一定不成立的是（ ）
A、(a + b) + c = a + (b + c) B、(a + b)·c = a·c + b·c
C、m(a + b) = ma +mb D、(a·b)c = a(b·c)
2、若a=(2，3)，b=(-4，7)，则a在b方向上的投影为（ ）
A、
B、
C、
D、
3、正方形ABCD边长等于1，
a，
b，
c，则a + b + c的模等于（ ）
A、0 B、
D、
4、已知△ABC中，
a，
b，a·b<0，
，a=3，b=5，则a与b的夹角为（ ）
A、30° B、-150° C、150° D、30°或150°
5、以
为顶点的三角形一定是（ ）
A、直角三角形 B、等腰直角三角形
C、锐角三角形 D、钝角三角形
6、已知a=2，b=，a与b的夹角为45°，要使
b-a与a垂直，则=
。
7、已知a=2
， b=（-2，3），且a⊥b，则a的坐标为 。
8、设a、b是两个不共线的非零向量
（1）若a与b起点相同，t为何值时，a，t b，
(a + b)三向量的终点在一直线上；
（2）若a=b且a与b的夹角为60°，那么t为何值时，a–t b的值最小？
9、向量
满足条件
，
，
求证
是等边三角形。
10、设两向量e1、e2满足e1=2，e2=1，e1、e2的夹角为60°，若向量2te1+7e2与向量e1+te2夹角为钝角，求实数t的取值范围。
知识升华
1、设向量a = (3，m)，b = (2，-1)，且a - 3b与a - b垂直，则实数m的值是（ ）
A、m=0 B、m=-4
C、m=0或m=-4 D、m=0或m=4
2、已知a⊥b，a=2，b=3，且3a+2b与a-b垂直，则等于（ ）
A、
B、
C、
D、1
3、设a、b是两个非零向量，则(a + b)2=a2+b2是a⊥b的（ ）
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既非充分又非必要条件
4、已知A、B、C三点共线，且
，若C点的横坐标为6，则它的纵坐标为（ ）
A、
B、13 C、9 D、
5、在△ABC中，若
a，
b，
c且a·b=b·c=c·a，则△ABC的形状是（ ）
A、等腰三角形 B、直角三角形 C、等边三角形 D、不确定
6、已知△ABC中，顶点A、B、C所对的边分别是a、b、c，a=3，b=1，c=30°，则
等于（ ）
A、
B、
C、
D、
7、已知四个点
，则对四边形ABCD的形状的判定是（ ）
A、梯形 B、邻边不相等的平行四边形
C、菱形，但非正方形 D、正方形
8、已知向量a=3e1-2e2，b=4e1+e2，e1=(1,0)，e2=(0,1)，则a + b= 。
9、已知a=，b=3，a与b夹角为45°，求使向量a+b与a + b的夹角是锐角时，的取值范围是 。
10、设
为首项是-10，公差是2的等差数列，
为首项是
，公差是
的等差数列，O为坐标原点，向量
，点列
满足
（1）证明：
共线；
（2）若点
表示点列中处于第一象限的点，求的值。
11、设a
，b
，c
，a与c的夹角为
，b与c的夹角为
，且
，求
的值。
12、如图，在△OAB中，
，AD与BC交于M点，设
a，
b
（1）用a、b表示
；
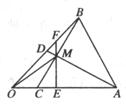（2）在已知线段AC上取一点E，在线段BD上取一点F，使EF过M点，设
，求证：
挑战高考
1、已知a、b均为单位向量，它们的夹角为60°，那么a+3b=（ ）
A、
B、
C、
D、4
2、若向量a与b的夹角为60°，b=4，(a+2b)(a-3b)=-72，则向量a的模为（ ）
A、2 B、4 C、6 D、12
3、已知a、b是非零向量且满足(a-2b)⊥a，(b-2a)⊥b，则a与b的夹角是（ ）
A、
B、
C、
D、
4、已知平面上直线l的方向向量e=
，点和
在l上的射影分别是O/和A/，则
，其中
（ ）
A、
B、
C、2 D、-2
5、给出下列命题：
①若a·b=0，则a=0或b=0；
②若e为单位向量，且a e，则a=a e；
③a·a·a=a3；
④若a与b共线，b与c共线，则a与c共线。其中正确命题的个数是
A、0 B、1 C、2 D、3
6、已知向量a与b不共线，且a=b
0，则下列结论中正确的是（ ）
A、向量a + b与a-b垂直 B、向量a-b与a垂直
C、向量a + b与a垂直 D、向量a + b与a-b共线
7、已知向量
，则
与
夹角的范围是（ ）
A、
B、
C、
D、
8、设i、j是不共线的单位向量，a=5i+3j，b=3i - 5j，则a⊥b是i⊥j的（ ）
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既非充分又非必要条件
9、已知向量
，在x轴上一点P使
有最小值，则P点的坐标是（ ）
A、
B、
C、
D、
10、锐角三角形ABC中，已知
，三角形ABC的面积为，则
的值为（ ）
A、2 B、
C、4 D、
11、已知向量a=(1，1)，b=(2，-3)，若ka-2b与a垂直，则实数k等于 。
12、平面向量a，b中，已知a=(4，-3)，b=1，且a·b = 5，则向量b= 。
13、已知平面直角坐标系
中，向量j = (0，1)，△OFP的面积为
，且
j
（1）设
，求向量
与
的夹角
的取值范围；
（2）设以原点O为中心，对称轴在坐标轴上，以F为右焦点的椭圆经过点M，且
，当
取最小值时，求椭圆的方程。
14、设在平面上有两个向量a=
，b=
（1）试证：两向量a + b与a - b垂直；
（2）两个向量ka + b与a – kb (k0)的模相等时，求解
15、已知向量a =
，b =
，x = a+(
-3)b，y =-ka + tb，且x·y = 0
（1）求函数的表达式；
（2）若
，求
的最大值与最小值。
16、已知向量a =
b =
c =(0，1),
（1）向量a，b是否共线？请说明理由；
（2）求函数
的最大值。
17、已知向量a=
，b=
，
，d=
，又二次函数
的图象开口向上，其对称轴为
，当
时，求使不等式f (a·b)> f (c·d)成立的x的范围。
18、已知O为坐标原点，
是常数
，若
（1）求
关于
的函数解析式；
（2）若
时，的最大值为2，求
的值并指出的单调区间。