第三节三角函数的图象和性质
【例1】试求函数![]() 的定义域。
的定义域。
【例2】(1)求函数![]() 的定义域;
的定义域;
(2)求函数![]() 的值域;
的值域;
(3)已知![]() ,求
,求![]() 的最大值和最小值。
的最大值和最小值。
【例3】判断下列函数的奇偶性:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() 。
。
【例4】下列四个函数中以π为最小正周期,且在区间![]() 上为减函数的是( )
上为减函数的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
【例5】比较下列各组数的大小:
(1)![]() 与
与![]() ;
;
(2)![]() 、
、![]() 、
、![]() ;
;
(3)![]() 与
与![]() 。
。
【例6】已知函数![]()
(1)求函数![]() 的最小正周期和最大值;
的最小正周期和最大值;
(2)在给出的直角坐标系中,画出函数![]() 在区间
在区间![]() 上的图象。
上的图象。
【例7】(1)指出经过怎样的图象变换,函数![]() 的图象可以变换成为函数
的图象可以变换成为函数![]() 的图象?
的图象?
(2)指出经过怎样的图象变换,函数![]() 的图象可以变换成为函数
的图象可以变换成为函数![]() 的图象?
的图象?
(3)由(1)、(2)可以受到怎样的启示?
【例8】(1)已知函数![]()
![]() 图象上的一个最高点为
图象上的一个最高点为![]() ,由这个最高点到相邻最低点间的曲线与
,由这个最高点到相邻最低点间的曲线与![]() 轴相交于点
轴相交于点![]() 。
。
①求这个函数的表达式;
②求这个函数的单调区间。
(2)如下图:某地一天从6时至14时的温度变化曲线近似满足函数![]()
①求这段函数的最大温差;
②写出这段曲线的函数解析式。
【例9】如果函数![]() 的图象关于直线
的图象关于直线![]() 对称,那么
对称,那么![]() =_____
=_____
双基训练
1、函数![]() 的值域为______________________
的值域为______________________
2、函数![]() 的定义域为__________________
的定义域为__________________
3、函数![]() 的值域是________________
的值域是________________
4、若![]() ,则
,则![]() 的取值范围是____________
的取值范围是____________
5、函数![]() 的值域为________________
的值域为________________
6、![]() 的最大值为_________________
的最大值为_________________
7、函数![]() 为常数),若
为常数),若![]() ,则
,则![]() 的最大值为_____
的最大值为_____
8、已知如右图:是函数![]() 的图象。
的图象。
(1)求![]() 、
、![]() 的值;
的值;
(2)求函数图象的对称轴的方程。
9、试求函数![]() 的定义域。
的定义域。
10、如下图:为正弦函数![]() 的一个周期的图象。
的一个周期的图象。
(1)写出![]() 的解析式;
的解析式;
(2)写出![]() 的解析式,使得
的解析式,使得![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称。
对称。
知识升华
1、设![]() ,若
,若![]() ,且
,且![]() ,那么
,那么![]() 的取值范围是______
的取值范围是______
2、函数![]() 的最大值为__________
的最大值为__________
3、对于函数![]() ,其中
,其中![]() 均为不等于零的常数,以下有四种说法:①最大值为A;②最小正周期为
均为不等于零的常数,以下有四种说法:①最大值为A;②最小正周期为![]() ;③在
;③在![]() 内,可以找到至少一个值
内,可以找到至少一个值![]() ,使
,使![]() ;④由
;④由![]()
![]() )解得
)解得![]() 的取值区间即为函数
的取值区间即为函数![]() 的单调递增区间。那么以上说法( )
的单调递增区间。那么以上说法( )
A、全对 B、有且只有一个是对的 C、全错 D、至少有两个是对的
4、要得到函数![]() 的图象只需将
的图象只需将![]() 的图象( )
的图象( )
A、向右平移![]() B、向左平移
B、向左平移![]() C、向右平移
C、向右平移![]() D、向左平移
D、向左平移![]()
5、若![]() ,则( )
,则( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
6、函数![]() 的图象关于
的图象关于![]() 轴对称的充要条件是( )
轴对称的充要条件是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]() 其中(
其中(![]() )
)
7、设![]() 是某港口水的深度
是某港口水的深度![]() (米)关于时间
(米)关于时间![]() (小时)的函数,其中
(小时)的函数,其中![]() ,下表是该港口某一天从0时至24时记录的时间
,下表是该港口某一天从0时至24时记录的时间![]() 与水深
与水深![]() 的关系:
的关系:
|
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
|
| 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
经长期观察,函数![]() 的图象可以近似地看成函数
的图象可以近似地看成函数![]() 的图象。下面的函数中最能近似地表示表中数据间对应关系的函数是:
的图象。下面的函数中最能近似地表示表中数据间对应关系的函数是:
A、![]() ,
,![]() B、
B、![]() ,
,![]()
C、![]() ,
,![]() D、
D、![]() ,
,![]()
8、将函数![]() 的图象向左平移
的图象向左平移![]() 个单位得到曲线
个单位得到曲线![]() ,又曲线
,又曲线![]() 与
与![]() 关于原点对称,则曲线
关于原点对称,则曲线![]() 的解析式是______________________
的解析式是______________________
9、设函数![]() ,给出下列关于
,给出下列关于![]() 的四个论断:
的四个论断:
①![]() 的图象关于直线
的图象关于直线![]() 对称;②
对称;②![]() 的图象关于点
的图象关于点![]() 对称;③
对称;③![]() 的最小正周期是
的最小正周期是![]() ;④
;④![]() 在区间
在区间![]() 内是单调递增。
内是单调递增。
以其中的两个论断作为条件,余下的两个论断作为结论构造命题,其中一个正确的命题是___________________
10、某港口水的深度![]() (米)是时间
(米)是时间![]() (小时)
(小时)![]() 的函数,记作
的函数,记作![]() ,下面是某日水深的数据:
,下面是某日水深的数据:
|
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
|
| 10.0 | 13.0 | 9.9 | 7.0 | 10.0 | 13.0 | 10.1 | 7.0 | 10.0 |
经长期观察,![]() 的曲线可以近似地看成函数
的曲线可以近似地看成函数![]() 的图象
的图象
(1)试根据以上数据,求出函数![]() 的近似表达式;
的近似表达式;
(2)一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可),某船吃水深度(船底离水面的距离)为6.5米,如果该船希望在同一天内安全进出港,请问:它至多能在港内停留多长时间(忽略进出港所需的时间)?
11、已知函数![]() 是R 上的偶函数,其图象关于点
是R 上的偶函数,其图象关于点![]() 对称,且在
对称,且在![]() 上是单调函数,求
上是单调函数,求![]() 和
和![]() 的值。
的值。
12、已知函数![]() ,
,![]() ,
,![]() 。若定义在非零实数值上的奇函数
。若定义在非零实数值上的奇函数![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,求当
,求当![]() 时,数
时,数![]() 的取值范围。
的取值范围。
挑战高考
1、函数![]() 的图象的一个对称中心是( )
的图象的一个对称中心是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、若![]() 是周期为
是周期为![]() 的奇函数,则
的奇函数,则![]() 可以是( )
可以是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、设![]() 是定义在R上的最小正周期为
是定义在R上的最小正周期为![]() 的函数,
的函数,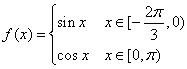 ,则
,则![]() 的值为( )
的值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、定义在R上的函数![]() 既是偶函数又是周期函数,若
既是偶函数又是周期函数,若![]() 的最小正周期是
的最小正周期是![]() ,且当
,且当![]() 时,
时,![]() ,则
,则![]() =_____________
=_____________
5、函数![]() 的最小正周期是______________
的最小正周期是______________
6、已知函数![]() 的图象过点
的图象过点![]() ,则
,则![]() 的值可以是( )
的值可以是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、函数![]() 是奇函数的充要条件是________________
是奇函数的充要条件是________________
8、函数![]() 的图象关于( )
的图象关于( )
A、点![]() 对称
B、点
对称
B、点![]() 对称
对称
C、直线![]() 对称 D、直线
对称 D、直线![]() 对称
对称
9、函数![]() 的图象中相邻两条对称轴的距离是__________
的图象中相邻两条对称轴的距离是__________
10、关于![]() 的函数
的函数![]() 有以下命题:
有以下命题:
①对任意的![]() ,
,![]() 都是非奇非偶函数;
都是非奇非偶函数;
②不存在![]() ,使
,使![]() 既是奇函数又是偶函数;
既是奇函数又是偶函数;
③存在![]() ,使
,使![]() 是偶函数;
是偶函数;
④对任意的![]() ,
,![]() 都不是奇函数。
都不是奇函数。
其中一个假命题的序号是______________,因为当![]() =_________时,该命题的结论不成立
=_________时,该命题的结论不成立