第四节三角函数的最值
【例1】求下列函数的值域：
①
；②
【例2】求下列函数的值域：
（10
；（2）
；（3）
【例3】已知
，求函数
的最大值和最小值，并求出此时
的值。
【例4】①求函数
的最小值、最大值、最小正周期。
②已知函数
（1）求
的最小正周期；
（2）若
，求的最大、最小值。
【例5】欲修建一横断面为等腰梯形的水渠，为降低成本，必须尽量减少水与水渠壁的接触面，若水渠断面面积设计为定值S，渠深8，则水渠壁的倾角
为多少时，才能使修建成本最低？
【例6】某体育馆拟用运动场的边角地建一个矩形的健身房，如右图：ABCD是一块边长为50m的正方形地皮，扇形CEF是运动场的一部分，其半径为40m。矩形AGHM就是拟建的健身室，其中G、M分别在AB和AD上，H在
上，设矩形AGHM的面积为S，
，请将S表示为
的函数，并指出当点H在的何处时，该健身室的面积最大，最大面积是多少？
双基训练
1、函数
在区间
上的最小值是____________
2、已知
，则
的最大值为_______；最小值为______
3、函数
的周期、最大值、初相依次是________、_______、_______
4、当
时，函数
的最小值是____________
5、设
，
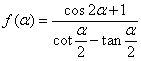，则
取最大值时，
＝_______
6、设函数
（
为常数）的最大值为1，最小值为－7，则
的最大值为_________
7、函数
，满足
，
，则
＝________
8、求函数
的最大值和最小值。
9、已知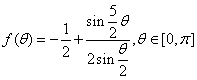
。
（1）将
表示成
的多项式；
（2）试求使曲线
与曲线
至少有一个公共点的的范围。
10、如右图所示：已知半径为1，圆心角为
的扇形，求一边在半径上的扇形的内接矩形的最大面积。
知识升华
1、函数
在区间
上的最大、最小值为________、________
2、函数
，当
时的值域为_______