第一学期高三质量调研测试数学试卷
数 学 试 卷
考生注意：
1． 答卷前，考生务必将学校、班级、学号、姓名等填写清楚．
2． 本试卷共有22道题，满分150分，考试时间120分钟．请考生用钢笔或圆珠笔书写，请不要将答案写在试卷的密封线以内．
3． 使用新教材的考生请注意符号说明：
| 符号意义 | 本试卷所用符号 | 等同于新教材符号 |
| 向量 |
|
|
| 正切 |
|
|
| 题 号 | 一 | 二 | 三 | 总 分 | |||||||||
| 1-12 | 13-16 | 17 | 18 | 19 | 20 | 21 | 22 | ||||||
| 得 分 | |||||||||||||
一．填空题（本大题满分48分）本大题共有12题，只要求直接填写结果，每个空格填对得4分，否则一律得零分．
1．设角
的终边过点
，则
______________．
2．
(
为虚数单位)的运算结果是_______________．
3．不等式
的解是__________________________．
4．设
是定义在
上的奇函数，则
的图像过定点_________________．
5．已知函数
，则
_______________．
6．计算：
=_______________．
7．设函数满足：对任意的
，都有
，则
与
的大小关系是______________________．
8．等差数列
中，
，则
____________．
9．矩形的面积与其周长的数值相等，则矩形面积的最小值是___________．
10．关于
的不等式
的解集为
，则复数
所对应的点位于复平面内的第________象限．
11．函数
图像上至少存在不同的三点到原点的距离构成等比数列，则公比的取值范围是_________________________.
12．在一次产品质量抽查中，某批次产品被抽出10件样品进行检验，其中恰有两件不合格品．如果对这10件样品逐个进行检验，则这两件不合格品恰好在第五次被全部检出的概率是______________（结果用分数表示）．
二．选择题（本大题满分16分）本大题共有4题，每题都给出代号为A、B、C、D的四个结论，其中有且只有一个结论是正确的，必须把正确的代号写在题后的圆括号内，选对得4分，不选、选错或者选出的代号超过一个（不论是否都写在圆括号内），一律得零分.
13．设
是两个非零向量，则“
”是“
”成立的
A．充要条件． B．必要不充分条件．
C．充分不必要条件． D．既不充分也不必要条件．
[答]（ ）
14．
内角分别是
，若关于的方程
有一个根为1，则一定是
A．等腰直角三角形． B．直角三角形．
C．等腰三角形． D．等边三角形．
[答]（ ）
15．
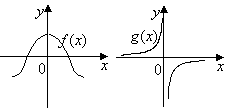设函数
与函数
的图像
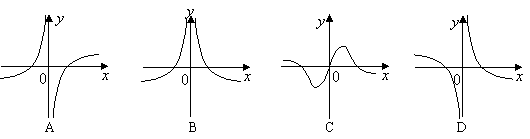如右图所示，则函数
的图
像可能是下面的
[答]（ ）
16．若不等式
对于任意正整数
恒成立，则实数
的取值范围是
A．
． B．
．
C．
．
D．
．
[答]（ ）
三. 解答题（本大题满分86分）本大题共有6题，解答下列各题必须写出必要的步骤.
17.（本题满分12分）
已知复数
是实系数一元二次方程
的一个根，向量
、
，求实数
和
使得
．
18.（本题满分12分）
设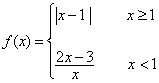
，解不等式
.
19.（本题满分14分）本题共有2个小题，
每小题满分各7分.
已知三个顶点分别是A（3，0）、B（0，3）、C
，
其中
．
（1）若
，求角的值；
（2）若
，求
的值．
20.（本题满分14分）本题共有2个小题，
第1小题满分6分，第2小题满分8分.
为了缓解交通压力，某省在两个城市之间特修一条专用铁路，用一列火车作为公共交通车．如果该列火车每次拖4节车厢，每日能来回16趟；如果每次拖7节车厢，则每日能来回10趟．火车每日每次拖挂车厢的节数是相同的，每日来回趟数y是每次拖挂车厢节数x的一次函数，每节车厢满载时能载客110人．
（１） 求出y关于x的函数关系式；
（２） 这列火车满载时每次应拖挂多少节车厢才能使每日营运人数最多?并求出每天最多的营运人数．
21.（本满分16分）本题共有3个小题，
第1、3小题满分各5分，第2小题满分6分.
如果一个数列的各项都是实数，且从第二项开始，每一项与它前一项的平方差是相同的常数，则称该数列为等方差数列，这个常数叫这个数列的公方差．
(1)设数列是公方差为
的等方差数列，求
和
的关系式；
(2)若数列既是等方差数列，又是等差数列，证明该数列为常数列；
(3) 设数列是首项为
，公方差为的等方差数列，若将
这种顺
序的排列作为某种密码，求这种密码的个数．
22.（本题满分18分）本题共有3个小题，
第1小题满分5分，第2小题满分6分，
第3小题满分7分.
已知函数
，当点
在的图像上移动时，
点
在函数
的图像上移动．
（1） 若点P坐标为（
），点Q也在的图像上，求的值；
（2） 求函数的解析式；
（3） 当
时，试探求一个函数
使得
在限定定义域为
时有最小值而没有最大值．