第七节函数的最值
【例1】求下列函数的值域：
（1）
；（2）
；（3）
【例2】求下列函数的最值
（1）
； （2）
； （3）
；
（4）
； （5）
。
【例3】已知函数
的定义域是R，值域为
，求实数
、
的值。
【例4】求函数
的值域。
【例5】设函数
为奇函数，对任意
，都有
，且
时，
，求在
上的最大值和最小值。
【例6】某疏菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿市场售价与上市时间的关系用图（1）的一条折线表示；西红柿的种植成本与上市时间的关系用图（2）的抛物线段表示。
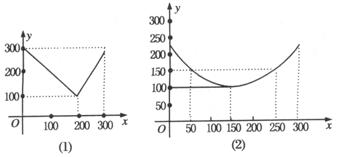
（I）写出图（1）表示的市场售价与时间的函数关系式
；写出图（2）表示的种植成本与时间的函数关系式
。
（II）认定市场售价减去种植成本为纯收益，问何时上市的西红柿纯收益最大？（注：市场售价和种植成本的单位：元/102kg，时间单位：天）
双基训练
1、设函数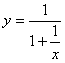
的定义域是M，值域是N，那么（ ）
A、
B、
C、
D、
2、函数
的值域是（ ）
A、
B、 C、
D、
3、函数
的值域是（ ）
A、
B、
C、
D、R
4、函数
的值域是（ ）
A、
B、
C、
D、
5、函数
的有（ ）
A、最小值为0，最大值为4 B、最小值为-4，最大值为0
C、最小值为-4，最大值为4 D、最小值与最大值都不存在
6、已知
，则
的最小值是
。
7、已知
，则
的最小值是
。
8、设
为正常数，且
，求
的最小值。
9、求函数
的最值。
10、已知
（1）若设
，试用
、
表示
；
（2）若当
时，有最小值8，求和
的值。
知识升华
1、如果
，那么
（ ）
A、无最大值也无最小值 B、无最大值而有最小值
C、有最大值而无最小值 D、有最大值也有最小值
2、某产品的总成本y（万元）与产量x（台）之间的函数关系式是
若每台产品的售价为25万元，则生产者不亏本时（销售收入不
小于总成本）的最低产量是（ ）
A、100台 B、120台 C、150台 D、180台
3、函数
的最小值是0，则的取值范围是（ ）
A、（0,1） B、（1，2） C、(1，+
） D、
4、若，则
的最大值为（ ）
A、6 B、5 C、4 D、3
5、若
，且
，那么
的最小值为（ ）
A、2 B、
C、
D、0
6、已知
，则S的最小值是（ ）
A、0 B、2 C、4 D、
7、函数
的最小值是（ ）
A、
B、
C、3 D、2
8、若函数
在
上的最大值与最小值之差为2，则
。
9、方程
表示的曲线到轴距离的最小值为
。
10、渔场中鱼群的最大养殖量为m吨，为保证鱼群的生长空间，实际养殖量不能达到最大养殖量，必须留出适当空间量，已知鱼群的年增长量吨和实际养殖量吨与空间率的乘积成正比，比例系数为
。
（1）写出与的函数关系式，并指出这个函数的定义域；
（2）求鱼群年增长量的最大值；
（3）当鱼群的年增长量达到最大值时，求
的最值范围。
11、设为实数，函数
。
（1）讨论的奇偶数；
（2）求的最小值。
12、已知某厂生产件产品的成本为
，问：
（1）要使平均成本最低，应生产多少件产品？
（2）若产品以每件500元售出，要使利润最大，应生产多少件产品？
挑战高考
1、对于任意实数
表示
中较小的那个数，当
时取它们相等的值，若
，则
的最大值是（ ）
A、1 B、-2 C、2 D、-1
2、今有一组实验数据如下：
|
| 1.993 | 3.002 | 4.001 | 5.032 | 6.121 |
|
| 1.501 | 4.413 | 7.498 | 12.04 | 17.98 |
现准备用下列函数中的一个，近似地表示数据满足的规律，其中接近的是（ ）
A、
B、
C、
D、
3、在
上，函数
在同一点取得相同的最小值，那么在上的最大值是（ ）
A、2 B、3 C、4 D、5
4、已知
是偶函数，当
时，
，且当
时，
恒成立，则
的最小值是（ ）
A、
B、 C、1 D、
5、对于函数
，规定当
时，
，当
时，
，已知
，则
的最大值为
。
6、已知函数
。
（1）求的反函数；
（2）如果不等式
对于
上的每一个的值都成立，求实数的取值范围。
（3）设
，求实数
的最小值及相应的值。
7、已知
，函数
在定义域上是偶函数，函数
在
上是减函数，在
上是增函数
①求：
②求
：
③如果在区间
上存在函数
满足
，当为何值时，取值最小值，并求此最小值。
8、已知函数对任意的实数
都有
，且
。
（I）若
，试求的表达式；
（II）若
时，不等式
恒成立，求实数的取值范围。