第三节反函数
【例1】求函数![]() 的反函数,并在同一坐标系中画出它们的图象。
的反函数,并在同一坐标系中画出它们的图象。
【例2】求下列函数的反函数:
(1)![]() ;(2)
;(2)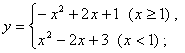
(3)![]()
【例3】已知函数![]() 的反函数为
的反函数为![]() ,则
,则![]()
。
【例4】若点![]() 既在函数
既在函数![]() 的图象上,又在反函数
的图象上,又在反函数![]() 的图象上,试确定
的图象上,试确定![]() 和
和![]() 的解析式。
的解析式。
【例5】已知函数![]() 的反函数,记
的反函数,记![]() ,求:
,求:
(1)![]() 的定义域和单调区间; (2)
的定义域和单调区间; (2)![]() 的最小值。
的最小值。
【例6】给定实数![]() ,函数
,函数![]()
(1)证明:函数的图象关于直线![]() 对称;
对称;
(2)若函数的图象与直线![]() 无公共点,求实数
无公共点,求实数![]() 的取值范围。
的取值范围。
双基训练
1、已知![]() 的反函数为
的反函数为![]() ,则
,则![]() 的值为( )
的值为( )
A、![]() B、0 C、4 D、8
B、0 C、4 D、8
2、已知![]() 的图象经过点
的图象经过点![]() 的反函数为
的反函数为![]() ,则
,则![]() 的图象必经过点( )
的图象必经过点( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、已知![]() 的反函数为
的反函数为![]() ,而函数
,而函数![]() 的图象与
的图象与![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() 的值为( )
的值为( )
A、5 B、![]() C、
C、![]() D、
D、![]()
4、函数![]() 有反函数
有反函数![]() ,将
,将![]() 的图象绕原点顺时针方向旋转
的图象绕原点顺时针方向旋转
90º后得到另一个函数的图象,则得到的这个函数是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、已知函数![]() ,函数
,函数![]() 的图象与函数
的图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() 等于( )
等于( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、函数![]() 的反函数是 。
的反函数是 。
7、设![]() ,则
,则![]() 。
。
8、已知函数![]() 的图象关于直线
的图象关于直线![]() 对称,求实数
对称,求实数![]() 的值。
的值。
9、设函数![]() 满足
满足![]() ,求
,求![]()
10、求函数![]() 与它的反函数的交点坐标。
与它的反函数的交点坐标。
知识升华
1、已知函数![]() 有反函数
有反函数![]() ,则函数
,则函数![]() 与函数
与函数![]() 的图象( )
的图象( )
A、关于原点对称 B、关于![]() 轴对称
轴对称
C、关于直线![]() 对称 D、关于直线
对称 D、关于直线![]() 对称
对称
2、函数![]() 的反函数是( )
的反函数是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
3、函数![]() 的反函数是( )
的反函数是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
4、已知函数![]() 的反函数是
的反函数是![]() ,则函数
,则函数![]() 的图象是( )
的图象是( )
5、已知函数![]() ,其反函数
,其反函数![]() 的图象的对称中心是
的图象的对称中心是![]() ,则实数
,则实数![]() 等于( )
等于( )
A、2 B、3 C、-2 D、-4
6、设三个函数,第一个函数是![]() ,它的反函数就是第二个函数,而第三个函数的图象与第二个函数图象关于直线
,它的反函数就是第二个函数,而第三个函数的图象与第二个函数图象关于直线![]() 对称,那么第三个函数是( )
对称,那么第三个函数是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
![]()
7、函数![]() 的反函数( )
的反函数( )
A、是奇函数,它在![]() 上是减函数
上是减函数
B、是偶函数,它在![]() 上是减函数
上是减函数
C、是奇函数,它在![]() 上是增函数
上是增函数
D、是偶函数,它在![]() 上是增函数
上是增函数
8、已知函数![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() 。
。
9、函数![]() 的图象与其反函数的图象有公共点,则实数
的图象与其反函数的图象有公共点,则实数![]() 的取值范围是 。
的取值范围是 。
10、已知![]()
(1)求它的反函数![]() ;
;
(2)若函数![]() 的图象关于直线
的图象关于直线![]() 对称,求
对称,求![]() 的值;
的值;
(3)若![]() ,求
,求![]() 的值。
的值。
11、已知定义域为R+的函数![]() ,对于任意
,对于任意![]() 时,恒有
时,恒有![]()
(1)求证:当![]() 时,
时,![]() ;
;
(2)若![]() 时,恒有
时,恒有![]() ,求证:
,求证:![]() 必有反函数;
必有反函数;
(3)设![]() 是
是![]() 的反函数,求证:
的反函数,求证:![]() 在其定义域内恒有
在其定义域内恒有![]()
![]()
12、设![]() ,
,![]() 为奇函数,且
为奇函数,且![]()
(1)试求![]() 的反函数
的反函数![]() 及其定义域;
及其定义域;
(2)设![]() ,若
,若![]() 时,
时,![]() 恒成立,试求实数
恒成立,试求实数![]() 的范围。
的范围。
挑战高考
1、设函数![]() ,满足
,满足![]() ,则
,则![]() 的值是( )
的值是( )
A、![]() B、
B、![]() C、
C、![]() D、2
D、2
2、已知函数![]() ,则其反函数
,则其反函数![]() =( )
=( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
3、设函数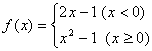 ,则
,则![]() 的值是( )
的值是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、设![]() 是函数
是函数![]() 的反函数,则以下不等式中恒成立的是( )
的反函数,则以下不等式中恒成立的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
5、记函数![]() 的反函数为
的反函数为![]() ,则
,则![]() ( )
( )
A、2 B、![]() C、3 D、
C、3 D、![]()
6、函数![]() 的反函数是( )
的反函数是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
7、函数![]() 的反函数
的反函数![]() 。
。