第三节含有绝对值的不等式
【例1】解关于x的不等式
。
【例2】解不等式
【例3】对任意实数x，若不等式
恒成立，则k的取值范围是（ ）
A、
B、
C、
D、
【例4】解关于x的不等式：
【例5】若二次不等式
的一切实数恒成立，求实数a的取值范围。
【例6】解下列不等式：
（1）
；
（2）
。
双基训练
1、下列不等式中解集为R的是（ ）
A、
B、
C、
D、
2、若
，则下列结论正确的是（ ）
A、
B、
C、
D、
3、若不等式
的解集为
，则实数a等于（ ）
A、8 B、2 C、-4 D、-8
4、不等式
的最小正整数解是（ ）
A、0 B、-1 C、1 D、2
5、不等式
的解集是（ ）
A、
B、
C、
D、
6、不等式
的解集是
。
7、不等式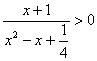
的解集是
。
8、解下列不等式：
（1）
；
（2）
。
9、解下列关于x的不等式：
（1）
；
（2）
。
10、p为何值时，不等式
对任意实数x恒成立。
知识升华
1、集合
的真子集的个数为（ ）
A、7 B、8 C、15 D、16
2、若关于x的不等式
的解集为
，则
的取值范围是（ ）
A、
B、
C、
D、
3、不等式
的解集是
则
等于（ ）
A、10 B、-10 C、14 D、-14
4、关于x的不等式
的解集为，则（ ）
A、
B、
C、
D、
5、设二次函数
，如果
，则
等于（ ）
A、
B、
C、
D、
6、不等式
的解集是（ ）
A、
B、
C、
D、
7、不等式
的解集是（ ）
A、
B、
C、
D、
8、若不等式
的解集是
，则实数a的值
为 。
9、若关于x的不等式
有解，且解的区间长度不超过5个单位，则实数a的取值范围是
。
10、已知集合
，若
，求实数a的值取范围。
11、已知关于x的不等式
解集是
，求不等式
的解集。
12、设集合
，若
，求实数k 的范围。
13、已知集合
，如果
，求实数m的取值范围。
挑战高考
1、不等式
的解集是（ ）
A、
B、
C、
D、
2、不等式
的解集是（ ）
A、
B、
C、
D、
3、已知
，则
的取值范围是（ ）
A、
B、
C、
D、
4、不等式
的解集为（ ）
A、
B、
C、
D、
5、不等式
的解集为（ ）
A、（0，1） B、
C、
D、
6、（理）已知不等式组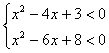
，的集是不等式
的解集的子集，则实数a的取值范围是 。
（文）若不等式
的解集为
，则实数的值为 。
7、（理）设函数
，其中
为常数。
（I）解不等式
；
（II）试推断函数
是否存在最小值？若存在，求出其最小值；若不存在，说明理由。
（文）设
，当
时，总有
，求证：
的解集解，求，
，