数学高考题选8——直线和圆(18+18)
1(06福建文1)(1)已知两条直线![]() 和
和![]() 互相垂直,则
互相垂直,则![]() 等于 ( D )
等于 ( D )
(A)2 (B)1 (C)0 (D)![]()
2(06福建文3)(3)![]() 是
是![]() 的
( B )
的
( B )
(A)充分而不必要条件 (B)必要不而充分条件
(C)充要条件 (D)既不充分也不必要条件
3(06天津理3文3)设变量![]() 、
、![]() 满足约束条件
满足约束条件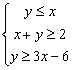 ,则目标函数
,则目标函数![]() 的最小值为 (B )
的最小值为 (B )
4(06广东9)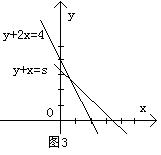 在约束条件
在约束条件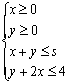 下,当
下,当![]() 时,
时,
目标函数![]() 的最大值的变化范围是
( D )
的最大值的变化范围是
( D )
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
解:由![]() 交点为
交点为
![]() ,
,
(1)
当![]() 时可行域是四边形OABC,此时,
时可行域是四边形OABC,此时,![]()
(2)
当![]() 时可行域是△OA
时可行域是△OA![]() 此时,
此时,![]()
故选D.
5(06浙江理4)
在平面直角坐标系中,不等式组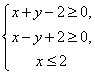 表示的平面区域的面积是( B )
表示的平面区域的面积是( B )
(A)![]() (B)4 (C)
(B)4 (C)![]() (D)2
(D)2
6(06浙江文9)在平面直角坐标系中,不等式组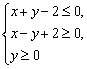 表示的平面区域的面积是 ( B )
表示的平面区域的面积是 ( B )
(A) ![]() (B)4
(C)
(B)4
(C) ![]() (D)2
(D)2
7(06安徽理10文10)如果实数![]() 满足条件
满足条件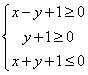 ,那么
,那么![]() 的最大值为( B )
的最大值为( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8(06山东理11)某公司招收男职员![]() 名,女职员
名,女职员![]() 名,
名,![]() 和
和![]() 须满足约束条件
须满足约束条件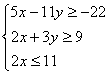 ,则
,则![]() 的最大值是
( C)
的最大值是
( C)
(A)80 (B)85 (C)90 (D)95
9(06山东文)(12)已知x和y是正整数,且满足约束条件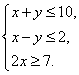 则
则![]() 的最小值是( B )
的最小值是( B )
(A)24 (B)14 (C)13 (D)11.5
10(06四川理)(8) 某厂生产甲产品每千克需用原料![]() 和原料
和原料![]() 分别为
分别为![]() ,生产乙产品每千克需用原料
,生产乙产品每千克需用原料![]() 和原料
和原料![]() 分别为
分别为![]() 千克,甲、乙产品每千克可获利润分别为
千克,甲、乙产品每千克可获利润分别为![]() 元,月初一次性够进本月用原料
元,月初一次性够进本月用原料![]() 各
各![]() 千克,要计划本月生产甲产品和乙产品各多少千克才能使月利润总额达到最大;在这个问题中,设全月生产甲、乙两种产品分别为
千克,要计划本月生产甲产品和乙产品各多少千克才能使月利润总额达到最大;在这个问题中,设全月生产甲、乙两种产品分别为![]() 千克,
千克,![]() 千克,月利润总额为
千克,月利润总额为![]() 元,那么,用于求使总利润
元,那么,用于求使总利润![]() 最大的数学模型中,约束条件为
( C )
最大的数学模型中,约束条件为
( C )
(A)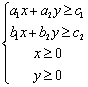 (B)
(B)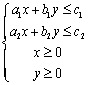 (C)
(C)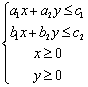 (D)
(D)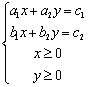
11(06重庆理3)过坐标原点且与圆![]() 相切的直线的方程为 ( A )
相切的直线的方程为 ( A )
(A)![]() 或
或![]() (B)
(B)![]() 或
或![]()
(C)![]() 或
或![]() (D)
(D)![]() 或
或![]()
12(06重庆文3)以点(2,-1)为圆心且与直线![]() 相切的圆的方程为 ( C )
相切的圆的方程为 ( C )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
13(06江苏2) 圆![]() 的切线方程中有一个是 ( C )
的切线方程中有一个是 ( C )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
14(06安徽文7)直线![]() 与圆
与圆![]() 没有公共点,则
没有公共点,则![]() 的取值范围是( A )
的取值范围是( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
15(06湖南理10) 若圆![]() 上至少有三个不同的点到直线
上至少有三个不同的点到直线![]() 的距离为
的距离为![]() ,则直线
,则直线![]() 的倾斜角的取值范围是 (B)
的倾斜角的取值范围是 (B)
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
16(06湖南文7)圆![]() 上的点到直线
上的点到直线![]() 的最大距离与最小距离的差是( C )
的最大距离与最小距离的差是( C )
A.36
B. 18
C. ![]() D.
D. ![]()
17(全国1文7)从圆 ![]() 外一点
外一点![]() 向这个圆作两条切线,则两切线夹角的余弦值为(B)
向这个圆作两条切线,则两切线夹角的余弦值为(B)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
18(06陕西理5文5).设直线过点![]() 其斜率为1,且与圆
其斜率为1,且与圆![]() 相切,则
相切,则![]() 的值为(B)
的值为(B)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二 填空题
1(06北京理13)已知点![]() 的坐标满足条件
的坐标满足条件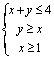 ,点
,点![]() 为坐标原点,那么
为坐标原点,那么![]() 的最小值等于__
的最小值等于__![]() ___,最大值等于____
___,最大值等于____![]() _________.
_________.
2 (06上海文9)已知实数![]() 满足
满足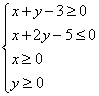 ,则
,则![]() 的最大值是___0______.
的最大值是___0______.
3 (06重庆文16) 已知变量![]() ,
,![]() 满足约束条件
满足约束条件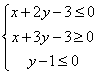 。若目标函数
。若目标函数![]() (其中
(其中![]() )仅在点
)仅在点![]() 处取得最大值,则
处取得最大值,则![]() 的取值范围为
的取值范围为 ![]() 。
。
4(06江苏12) 设变量![]() 满足约束条件
满足约束条件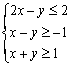 ,则
,则![]() 的最大值为
的最大值为 ![]()
5(06福建文)(15)已知实数![]() 、
、![]() 满足
满足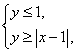 则
则![]() 的最大值是_4_。
的最大值是_4_。
6(06湖南理12文13)已知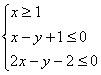 则
则![]() 的最小值是_____5______.
的最小值是_____5______.
7(全国1理14)设![]() ,式中变量
,式中变量![]() 满足下列条件
满足下列条件
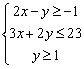 则z的最大值为______11_______。
则z的最大值为______11_______。
8(全国1文15)设![]() ,式中变量
,式中变量![]() 满足下列条件
满足下列条件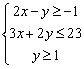 ,则
,则
z的最大值为___11_。
9(06四川文14) 设![]() 满足约束条件:
满足约束条件: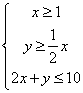 ,则
,则![]() 的最小值为__
的最小值为__![]() __;
__;
10(06北京文9) 若三点![]() 共线,则
共线,则![]() 的值等于
4 。
的值等于
4 。
11 (06上海文2)已知两条直线![]() 若
若![]() ,则
,则![]() __2__.
__2__.
12(06天津理14)设直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,且弦
两点,且弦![]() 的长为
的长为![]() ,则
,则![]() ______0____.
______0____.
13(06天津文14)若半径为1的圆分别与![]() 轴的正半轴和射线
轴的正半轴和射线![]() 相切,则这个圆的方程为
相切,则这个圆的方程为 ![]() .
.
14 (06上海理2)已知圆![]() -4
-4![]() -4+
-4+![]() =0的圆心是点P,则点P到直线
=0的圆心是点P,则点P到直线![]() -
-![]() -1=0的距离是
-1=0的距离是 ![]() .
.
15(06湖北理13)已知直线![]() 与圆
与圆![]() 相切,则
相切,则![]() 的值为 -18或8 。
的值为 -18或8 。
16(06湖北文13)
若直线y=kx+2与圆(x-2)2+(y-3)2=1有两个不同的交点,则k 的取值范围是 (0,![]() ) .
) .
17(06全国2理15文15) 过点(1,)的直线l将圆(x-2)2+y2=4分成两段弧,当劣弧所对的圆心角最小时,直线l的斜率k= .
18(06江西理16)已知圆M:![]()
直线![]() 下面四个命题:
下面四个命题:
A 对任意实数k与q,直线l和圆M相切;
B对任意实数k与q,直线l和圆M有公共点;
C对任意实数q,必存在实数k,使得直线l与和圆M相切
D对任意实数k,必存在实数q,使得直线l与和圆M相切
其中真命题的代号是___B,D____ (写出所有真命题的代号)
解:圆心坐标为![]()
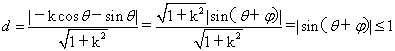
故选(B)(D)