高考能力测试步步高数学基础训练6

高考能力测试步步高数学基础训练6

基础训练6　函数的奇偶性、单调性、对称性

●训练指要

理解函数奇偶性、单调性的概念；掌握函数奇偶性、单调性的判定方法.

一、选择题

1.下列判断正确的是

A.f(x)=是奇函数

B.f(x)=(1-x)是偶函数

C.f(x)=lg(x+)是非奇非偶函数

D.f(x)=1既是奇函数又是偶函数

2.(2001年全国高考题)设f(x)、g(x)都是单调函数，有如下命题：

①若f(x)单调递增，g(x)单调递增，则f(x)-g(x)单调递增；

②若f(x)单调递增，g(x)单调递减，则f(x)-g(x)单调递增；

③若f(x)单调递减，g(x)单调递增，则f(x)-g(x)单调递减；

④若f(x)单调递减，g(x)单调递减，则f(x)-g(x)单调递减.

其中正确的命题是

A.①③　　　　　　　　　　　　 B.①④　　　　　　　　　　　　 C.②③　　　　　　　　　　　　 D.②④

3.已知f(x)是定义在R上的奇函数，当x<0时，f(x)=()^x,那么f()的值是

A. 　　　　　　　　　　　 B.-　　　　　　　　　　　　C.　　　　　　　　　　　　　D.-

二、填空题

4.函数y=(x²-6x+8)的单调递增区间是_________；单调递减区间是_________.

5.(2002年天津试题)设函数f(x)在(-∞,+∞)内有定义，下列函数①y=-f(x)　②y=xf(x²)　③y=-f(-x)　④y=f(x)-f(-x)中必为奇函数的有_________.(要求填写正确答案的序号)

三、解答题

6.函数f(x)对任意m、n∈R,都有f(m+n)=f(m)+f(n)-1,并且当x>0时，f(x)>1.

(1)求证f(x)是R上的增函数.

(2)设f(3)=4,解不等式f(a²+a-5)<2.

7.讨论函数f(x)=x+及g(x)=x-的单调性.

8.(2003年上海春季高考题)已知函数f(x)=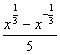,g(x)= .

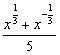(1)证明f(x)是奇函数，并求f(x)的单调区间.

(2)分别计算f(4)-5f(2)g(2)和f(9)-5f(3)g(3)的值.由此概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式，并加以证明.