高考能力测试步步数学基础训练2

高考能力测试步步数学基础训练2

基础训练2　绝对值不等式、整式不等式的解法

●训练指要

掌握一元二次不等式、整式不等式、分式不等式及绝对值不等式的解法.

一、选择题

1.(2003年安徽春季高考题)不等式1+x+<1的解集是

A.{x-1<x<0}　　　　　　　　　　　　　　　　　　　　　　B.{x-<x<0}

C.{x-<x<0}　　　　　　　　　　　　　　　　　　　　　D.{x-2<x<0}

2.(2003年北京春季高考题)若不等式ax+2<6的解集为(-1，2)，则实数a等于

A.8　　　　　　　　　　　　　　　B.2　　　　　　　　　　　 C.-4　　　　　　　　　　　D.-8

3.当a<0时，不等式42x²+ax-a²<0的解集为

A.{x-<x<}　　　　　　　　　　　　　　　　　　　 B.{x<x<-}

C.{x<x<-}　　　　　　　　　　　　　　　　　　　 D.{x-<x<}

二、填空题

4.若不等式ax²+bx+2>0的解集为{x-},则a+b=_________.

5.已知U=R，且A={x>0},B={x>0},则_U(A∪B)=_________.

三、解答题

6.(2003年上海春季高考题)解不等式组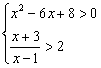

7.已知x-1≤2,且x-a≤2,求：

(1)当a<0时，求x的范围；

(2)若x的范围构成的集合是空集，求a的范围.

8.(2001年天津试题)解关于x的不等式：<0(a∈R).