高考全国统一标准数学测试（理科B卷）
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷（非选择题）两部分.共150分，考试用时120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题（本大题共12小题；每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）
1.设f(x)为奇函数，对任意x∈R，均有f(x+4)=f(x)，已知f(-1)=3，则f(-3)等于
A.3 B.－3 C.4 D.－4
2.已知直线l1：(a+1)x+y－2=0与直线l2：ax+(2a+2)y+1=0互相垂直，则实数a的值为
A.－1或2 B.－1或－2 C.1或2 D.1或－2
3.在等比数列{an}中，a1＞1，前n项和Sn满足
，那么a1的取值范围是
A.(1，+∞) B.(1，4) C.(1，2) D.(1，
)
4.已知m、l是异面直线，那么：①必存在平面α过m且与l平行；②必存在平面β过m且与l垂直；③必存在平面γ与m、l都垂直；④必存在平面π与m、l距离都相等，其中正确的结论为
A.①② B.①③ C.②③ D.①④
5.从装有4粒大小、形状相同颜色不同的玻璃球的瓶中，随意一次倒出若干粒玻璃球（至少一粒），则倒出奇数粒玻璃球的概率比倒出偶数粒玻璃球的概率
A.小 B.大
C.相等 D.大小不能确定
6.要得到函数y=sin2x的图象，可以把函数y=sin(2x－
)的图象
A.向左平移
个单位 B.向右平移个单位
C.向左平移个单位 D.向右平移个单位
7.设F1、F2是双曲线
－y2=1的两个焦点，点P在双曲线上，且
·
=0，则
的值为
A.0 B.2 C.2 D.4
8.设复数
－i，1－i的辐角主值分别为α、β，则α－β的值为
A.
B.
C.
D.－
9.设f(x)=
，利用课本中推导等差数列前n项和公式的方法，可求f(－5)+f(－4)
+f(－3)+…+f(4)+f(5)+f(6)等于
A.
B. C.2 D.3
10.已知函数f(x)是R上的增函数，A（0，－1），B（3，1）是其图象上的两点，那么f(x+1)＜1的解集是
A.（1，4） B.（－1，2）
C.（－∞，1］∪［4，+∞） D.（－∞，－1］∪［2，+∞）
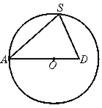11.过正三棱锥S—ABC的一条侧棱SA及其外接球的球心O，作棱锥截面SAD（如图）球心O在AD上，则此三棱锥的侧面三角形顶角的余弦值为
A.
B.0
C.－ D.
12.从盛装20升纯酒精的容器里，倒出一升纯酒精，然后用水加满，再倒出一升酒精混合液，再用水加满.照这样的方法继续下去，如果倒出第k次时共倒出纯酒精x升，则倒出第k+1次时，共倒出纯酒精f(x)的表达式是
A.f(x)=
x+1 B.f(x)=
+1
C.f(x)=(x+1) D.f(x)=
x
第Ⅱ卷 (非选择题 共90分)
二、填空题（本大题共4小题；每小题4分，共16分.把答案填在题中的横线上）
13.设f(x)=
，则f(
)+f(
)+…+f(
)的值为
.
14.如果曲线y=x3+x－10的某切线与直线y=4x+3平行，则此切线的方程为 .
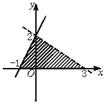15.如右图，表示图中平面区域的公共域的不等式组是
.
16.设函数f(x)=sin(ωx+
)(ω＞0，－＜＜)给出以下四个论断：
①它的图象关于x=
对称；②它的图象关于点(
，0)对称；③它的周期为π；④在区间［－，0）上是增函数，以其中两个论断作为条件，余下论断作为结论，写出你认为正确的两个命题：
（1） ；
（2） .
三、解答题(本大题共6小题；共74分.解答应写出文字说明、证明过程或演算步骤)
17.（本小题满分12分）
设复数z=3cosθ－2isinθ，π＜θ＜
，且θ－argz=.
（1）求tan(argz)；
（2）求使等式msin(θ+)=2cos2
－1成立的m值.
18.（本小题满分12分）
有一个问题，在半小时之内，甲能解决它的概率是，乙能解决它的概率是
.计算：
（1）两人都未解决的概率；
（2）问题得到解决的概率.
19.（本小题满分12分）
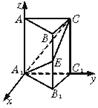
如图，正三棱柱ABC—A1B1C1中，E∈BB1，截面A1EC⊥侧面AC1.
（1）求证：
；
（2）若
，求平面A1EC与平面A1B1C1所成二面角的平面角（锐角）的大小.
20.（本小题满分12分）
某家用电器厂根据其产品在市场上的销售情况，决定对原来以每件2000元出售的一种产品进行调价，并按新单价的八折优惠销售.结果每件产品仍可获得实际销售价20%的利润.已知该产品每件的成本是原销售价的60%.
（1）求调价后这种产品的新单价是每件多少元？让利后的实际销售价是每件多少元？
（2）为使今年按新单价让利销售后的利润总额不低于20万元，今年至少应销售这种产品多少件？（每件产品利润=每件产品的实际销售价－每件产品的成本价）
21. (本小题满分14分)
设椭圆
=1(a＞b＞0)的焦点为F1、F2，P是椭圆上任一点，若∠F1PF2的最大值为
.
（1）求椭圆的离心率；
（2）设直线l与椭圆交于M、N两点且l与以原点为圆心，半径为短轴的圆相切.已知线段MN的长度最大值为4，求椭圆的方程与直线l的方程.
22.（本小题满分12分）
设函数f(x)是定义在［－1，0）∪（0，1］上的奇函数，当x∈［－1，0）时，f(x)=2ax+
（a∈R).
（1）当x∈(0，1］时，求f(x)的解析式；
（2）若a＞－1，试判断f(x)在（0，1］上的单调性，并证明你的结论；
（3）是否存在a，使得当x∈（0，1］时，f(x)有最大值－6.
参考答案
一、1.B 2.B 3.D 4.D 5.B 6.A 7.B 8.C 9.D 10.B 11.D 12.A
二、13. 5 14.y=4x－12或y=4x－8 15.
16.①③
②④ ②③①④
三、17.解：（1）由题设tan(argz)=
1分
∴tan(θ－argz)=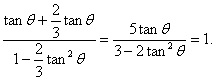
3分
即(2tanθ－1)(tanθ+3)=0，
又π<θ<；
∴tanθ=. 5分
则tan(argz)=－
8分
（2）由题意知，要使msin(θ+)=cosθ成立.
即要m(cosθ+sinθ)=cosθ成立.由于cosθ≠0
∴m(tanθ+1)=1. 8分
m=
，tanθ=，则m=
. 12分
18.解：（1）设在半小时内甲能独立解决该问题是事件A，乙能独立地解决该问题是事件B 2分
那么两个人都未解决该问题是事件
·
3分
由于两人是相互独立地求解，于是得到：
P（·）=P（）·P（）=（1－）（1－）=. 7分
（2）“问题得到解决”这一事件的概率为
1－P（·）=1－=. 12分
19.解：（1）如图建立坐标系，
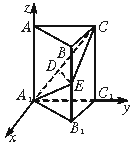
过E作ED⊥A1C，令D（0，y，z)，E(
a，c). 1分
则
=(－
a，y－a，z－c)，
=(0，a，b)，
=(0，0，b)， 2分
·=ay－a2+bz－bc， ①
·=bz－bc=0， ② 4分
②代入①得ay－a2=0，
∴y=a. 5分
∵D为A1C的中点，又ED⊥A1C，
∴△EA1C为等腰三角形.
∴EA1=EC，又A1B1=BC，∠EBC=∠A1B1E=90°.
∴△EBC≌△A1B1E.
∴
=
. 7分
（2）∵D（0， a，b)，E(a，a，b)，
∴
. 9分
∴
a2，又
，
∴b=a，
, 10分
.
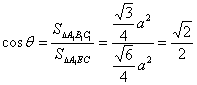∴θ=45°. 12分
20.解：（1）设每件产品的新单价为x元 1分
由已知：该产品的成本是2000×60%=1200元 2分
由题意：x·80%－1200=20%(80%·x) 4分
解得：x=1875(元）
∴80%·x=1500元 5分
所以，该产品调价后的新单价是每件1875元，
让利后实际售价为每件1500元. 6分
（2）设今年至少应生产这种电器m件，则由题意，
得m(1500－1200)≥200000 9分
解得：m≥666 10分
∵m∈N，∴m的最大值应为667件 11分
即今年至少售出667件产品，
才能使利润总额不低于20万元. 12分
21.解：∵椭圆方程为=1(a>b>0)
(1)PF1+PF2=2a
cosF1PF2=
3分
∴e= 5分
（2）∵e=，∴a2=4b2.
∴椭圆方程为y2+4x2=4b2 6分
该直线l：y=kx+m.
∵直线l与圆x2+y2=b2相切，∴m2=b2(1+k2) ①
从
得(4+k2)x2+2kmx+m2－4b2=0 8分
∵MN=4b·
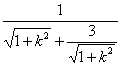≤2b
当且仅当k=±时取等号. 10分
∴l：y=±
. 12分
椭圆方程为：
=1. 14分
22.（1）解：设x∈(0，1］，则－x∈［－1，0)，f(－x)=－2ax+
，
∵f(x)是奇函数.
∴f(x)=2ax－，x∈(0，1］. 3分
（2）证明：∵f′(x)=2a+
， 5分
∵a>－1，x∈(0，1］，
>1，∴a+>0.
即f′(x)>0. 6分
∴f(x)在（0，1］上是单调递增函数. 7分
（3）解：当a>－1时，f(x)在（0，1］上单调递增.
f(x)max=f(1)=－6，
a=－
(不合题意，舍之）， 9分
当a≤－1时，f′(x)=0，x=
.
如下表：fmax(x)=f()=－6，解出a=－2.
x=∈(0，1) 10分
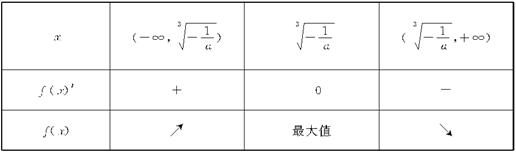
11分
∴存在a=－2，使f(x)在（0，1］上有最大值－6. 12分