高考全国统一标准数学测试(文科A卷)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试用时120分钟.
第Ⅰ卷(选择题 共60分)
参考公式:
sin![]() cos
cos![]() =
=![]() [sin(
[sin(![]() +
+![]() )+sin(
)+sin(![]() -
-![]() )]
)]
cos![]() sin
sin![]() =
=![]() [sin(
[sin(![]() +
+![]() )-sin(
)-sin(![]() -
-![]() )]
)]
cos![]() cos
cos![]() =
=![]() [cos(
[cos(![]() +
+![]() )+cos(
)+cos(![]() -
-![]() )]
)]
sin![]() sin
sin![]() =-
=-![]() [cos(
[cos(![]() +
+![]() )-cos(
)-cos(![]() -
-![]() )]
)]
sin![]() +sin
+sin![]() =2sin
=2sin![]() cos
cos![]()
sin![]() -sin
-sin![]() =2cos
=2cos![]() sin
sin![]()
cos![]() +cos
+cos![]() =2cos
=2cos![]() cos
cos![]()
cos![]() -cos
-cos![]() =-2sin
=-2sin![]() sin
sin![]()
S台侧=![]() (c′+c)l(c、c′分别表示上、下底面周长,l表示斜高或母线长)
(c′+c)l(c、c′分别表示上、下底面周长,l表示斜高或母线长)
V台体=![]() (S′+
(S′+![]() +S)h(S′、S分别表示上、下底面积,h表示高)
+S)h(S′、S分别表示上、下底面积,h表示高)
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么在n次独立重复试验中恰好发生k次的概率Pn(k)=C![]() pk(1-p)n-k
pk(1-p)n-k
一、选择题(本大题共12小题;每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.对于函数f(x)=lgsinx(![]() <x<
<x<![]()
![]() ,下列说法中正确的是
,下列说法中正确的是
A.f(x)是增函数,且f(x)>0 B.f(x)是增函数,且f(x)<0
C.f(x)是减函数,且f(x)>0 D.f(x)是减函数,且f(x)<0
2.设复数z1=2-i,已知z2=z1,且arg![]() ,则复数z2的值为
,则复数z2的值为
A.1+2i B.1-2i
C.-1+2i D.-1-2i
3.某地区高中分三类,A类校共有学生4000人,B类校共有学生2000人,C类校共有学生3000人.现欲抽样分析某次考试的情况,若抽取900份试卷进行分析,则从A类校抽取的试卷份数应为
A.450 B.400
C.300 D.200
4.给定两个向量a=(3,4),b=(2,1),若(a+xb)⊥(a-b),则x等于
A.-3 B.![]()
C.3 D.-![]()
5.对于定义在实数集R上的函数f(x),如果存在实数x0,使f(x0)=x0,那么x0叫做函数f(x)的一个不动点.已知函数f(x)=x2+2ax+1不存在不动点,那么a的取值范围是
A.(-![]() ) B.(-
) B.(-![]() )
)
C.(-1,1) D.(-∞,-1)∪(1,+∞)
6.直线y=x+5与曲线![]() =1的交点的个数是
=1的交点的个数是
A.0 B.1
C.2 D.3
7.点P在曲线y=x3-x+7上移动,过P点的切线的倾斜角取值范围是
A.[0,![]()
![]() B.(0,
B.(0,![]() )∪[
)∪[![]() ,
, ![]()
![]()
C.[0, ![]()
![]() ∪(
∪(![]() ,
,![]()
![]() D.[0,
D.[0, ![]()
![]() ∪[
∪[![]() ,
, ![]() )
)
8.在等比数列{an}中,已知对任意自然数n ,a1+a2+…+an=2n-1,则a12+a22+…+an2等于
A.(2n-1)2 B.![]() (2n-1)2
(2n-1)2
C.4n-1 D.![]() (4n-1)
(4n-1)
9.将一张坐标纸折叠一次,使点(0,5)与点(4,3)重合,则与点(-4,2)重合的点是
A.(4,-2) B.(4,-3)
C.(3,![]()
![]() ) D.(3,-1)
) D.(3,-1)
10.若偶函数f(x)在区间[-1,0]上是减函数,![]() 、
、![]() 是锐角三角形的两个内角,且
是锐角三角形的两个内角,且![]() ≠
≠![]() ,则下列不等式中正确的是
,则下列不等式中正确的是
A.f(cos![]() )>f(cos
)>f(cos![]() ) B.f(sin
) B.f(sin![]() )>f(cos
)>f(cos![]() )
)
C.f(sin![]() )>f(sin
)>f(sin![]() ) D.f(cos
) D.f(cos![]() )>f(sin
)>f(sin![]() )
)
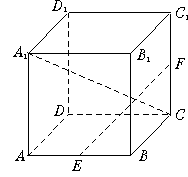
11.如下图,正方体ABCD—A1B1C1D1 中,E、F分别是AB、CC1的中点,则异面直线A1C与EF所成角的余弦值为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.甲、乙两人同时从A地出发沿同一路线走到B地,所用时间分别为t1、t2,甲有一半时间以速度m行走,另一半时间以速度n行走(m≠n);乙有一半路程以速度m行走,另一半路程以速度n行走.则下列结论成立的是
A.t1>t2 B.t1=t2
C.t1<t2 D.t1、t2的大小无法确定
第Ⅱ卷 (非选择题 共90分)
二、填空题(本大题共4小题;每小题4分,共16分.把答案填在题中的横线上)
13.若f(x)是R上的减函数,且f(x)的图象经过点A(0,3)和B(3,-1),则不等式f(x+1)-1<2的解集是____________.
14.已知f(x)=2x3-6x2+m(m为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值为____________.
15.设函数f(x)=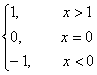 ,则方程x+1=(2x-1)f(x)的解为____________.
,则方程x+1=(2x-1)f(x)的解为____________.
16.如图所示,在A、B间有四个焊接点,若焊接点脱落,则可能导致电路不通. 今发现A、B之间线路不通,则焊接点脱落的不同情况有_________种.
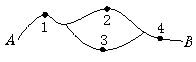
三、解答题(本大题共6小题;共74分.解答过程应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
已知f(x)=![]() ,
,
(Ⅰ)求f(x)的定义域、值域;
(Ⅱ)若f(x)=2,-![]() <x<
<x<![]() ,求x的值.
,求x的值.
18.(本小题满分12分)
在袋里装30个小球,其中彩球有:n个红色、5个蓝色、10个黄色,其余为白色.
求:(Ⅰ)如果已经从中取定了5个黄球和3个蓝球,并将它们编上了不同的号码后排成一排,那么使蓝色小球互不相邻的排法有多少种?
(Ⅱ)如果从袋里取出3个都是相同颜色彩球(无白色)的概率是![]() ,且n≥2,计算红球有几个?
,且n≥2,计算红球有几个?
(Ⅲ)根据(Ⅱ)的结论,计算从袋中任取3个小球至少有一个是红球的概率.
19.(本小题满分12分)
已知数列1,3,6…的各项是由一个等比数列和一个等差数列的对应项相加而得到,其中等差数列的首项为0.
(Ⅰ)求这个数列的前n项和Sn;
(Ⅱ)设Tn=![]() ,问是否存在正整数M,使得对一切正整数n,Tn≤M都成立.如存在,求出M的最小值;如不存在,说明理由.
,问是否存在正整数M,使得对一切正整数n,Tn≤M都成立.如存在,求出M的最小值;如不存在,说明理由.
(Ⅲ)求![]() Tn的值.
Tn的值.
20.(注意:在以下甲、乙两题中任选一题作答.如果两题都作答,只以甲题记分,本小题满分12分)
(甲)如图,已知正四棱锥S—ABCD,底面的中心O为坐标原点,建立空间直角坐标系O—xyz,其中Ox//BC、Oy//AB,四棱锥的底面的边长为4,高为6,点M是高SO的中点,G是侧面△SBC的重心.求
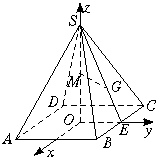
(Ⅰ)MG两点间的距离;
(Ⅱ)异面直线MG与BS所成的角.
(乙)如图,三棱锥P—ABC中,△ABC是正三角形,∠PCA=90°,D为PA的中点,二面角P—AC—B为120°,PC = 2,AB=2![]() .
.
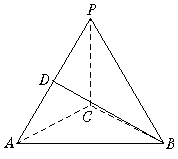
(Ⅰ)求证:AC⊥BD;
(Ⅱ)求BD与底面ABC所成角的正弦值.
21.(本小题满分12分)
给定双曲线x2-![]() =1,
=1,
(Ⅰ)过点A(2,1)的直线l与所给双曲线交于P1 、P2,求线段P1P2的中点P的轨迹方程;
(Ⅱ)过点B(1,1)能否作出直线l′,使l′与所给双曲线交于两点Q1 、Q2,且B是线段Q1Q2的中点?说明理由.
22.(本小题满分14分)
已知函数f(x)=x4-4x3+ax2-1在区间[0,1)上单调递增,在区间[1,2)上单调递减.
(Ⅰ)求a的值;
(Ⅱ)若点A(x0,f(x0))在函数f(x)的图象上,求证点A关于直线x=1的对称点B也在函数f(x)的图象上;
(Ⅲ)是否存在实数b,使得函数g(x)=bx2-1的图象与函数f(x)的图象恰有3个交点.若存在,请求出实数b的值;若不存在,试说明理由.
参 考 答 案
一、选择题
1.D
2.D (根据复数乘除法的几何意义)
3.B 4.A
5.A (已知条件等价于x2+2ax+1=x无实根,由此易得答案)
6.B (可用数形结合的方法,曲线![]() =1实际上是椭圆
=1实际上是椭圆![]() =1在一、四象限的部分和双曲线-
=1在一、四象限的部分和双曲线-![]() =1在二、三象限的部分)
=1在二、三象限的部分)
7.D (过P点的切线的倾斜角正切值的范围即是y′=3x2-1的值域[-1,+∞),由此得答案)
8.D
9.A (所求点是(-4,2)关于(0,5)与点(4,3)的中垂线的对称点)
10.B ( 由已知,![]() +
+![]() 是钝角,则有
是钝角,则有![]() >90°-
>90°-![]() ,而正弦函数在第一象限是增函数,
,而正弦函数在第一象限是增函数,
所以sin![]() >sin(90°-
>sin(90°-![]() ),即sin
),即sin![]() >cos
>cos![]() .
.
又偶函数f(x)在区间[-1,0]上是减函数,
所以函数f(x)在区间[0,1]上是增函数,因此选B)
11.B (设异面直线A1C与EF所成角为θ,正方体棱长为1,
![]() ,得
,得
![]() cosθ=1,所以选B)
cosθ=1,所以选B)
12.C (设A、B两地的路程为2s,则![]() t1m+
t1m+![]() t1n=2s和
t1n=2s和![]() =t2成立,
=t2成立,
由此得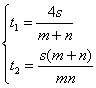 .由此易证t1<t2)
.由此易证t1<t2)
二、填空题
13.{x-1<x<2} 14.-37
15.x=0,2或-![]() 16.13
16.13
三、解答题
17.解:(Ⅰ)f(x)=![]()
=![]() 2分
2分
=![]() 3分
3分
=![]() . 4分
. 4分
由1+sin2x≠0,得sin2x≠-1,
∴2x≠2k![]() -
-![]() .∴x≠k
.∴x≠k![]() -
-![]() (k∈Z).
(k∈Z).
∴f(x)的定义域为{xx∈R,且x≠k![]() -
-![]() ,k∈Z}. 6分
,k∈Z}. 6分
∵0<1+sin2x≤2,∴![]() ≥
≥![]() .
.
∴f(x)的值域为{yy≥![]() }. 8分
}. 8分
(Ⅱ)由f(x)=2,即![]() =2,得sin2x=-
=2,得sin2x=-![]() . 9分
. 9分
∵-![]() <x<
<x<![]() ,-
,-![]() <2x<
<2x<![]() , 10分
, 10分
∴2x=-![]() 或2x=
或2x=![]() ,∴x=-
,∴x=-![]() 或x=
或x=![]() . 12分
. 12分
18.解:(Ⅰ)将5个黄球排成一排只有A![]() 种排法,将3个蓝球放在5个黄球所形成的6个空上,有A
种排法,将3个蓝球放在5个黄球所形成的6个空上,有A![]() 种放法 .
种放法 .
∴所求的排法为A![]() A
A![]() =5×4×3×2×6×5×4=14400(种). 4分
=5×4×3×2×6×5×4=14400(种). 4分
(Ⅱ)取3个球的种数为C![]() =4060,设“3个球全红色”为事件A,“3个球全蓝色”为事件B,“3个球全黄色”为事件C.
=4060,设“3个球全红色”为事件A,“3个球全蓝色”为事件B,“3个球全黄色”为事件C.
P(B)=![]() ,P(C)=
,P(C)=![]() .
.
∵A、B、C为互斥事件,
∴P(A+B+C)= P(A)+P(B)+P(C) ,
即![]()
![]() P(A)=0
P(A)=0![]() 红球的个数≤2.
红球的个数≤2.
又∵n≥2,故n=2. 8分
(Ⅲ)记“3个球中至少有一个是红球”为事件D,则![]() 为“3个球中没有红球”,
为“3个球中没有红球”,
P(D)=1-P(![]() )=1-
)=1-![]() 或P(D)=
或P(D)=![]() . 12分
. 12分
19.解:(Ⅰ)设数列1,3,6,…为{An},An=an+bn,其中{an}为等比数列,{bn}为等差数列,q、d分别为数列{an}、数列{bn}的公比与公差,而b1=0,且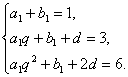
解之,得d1=1,q=2,a1=1.因而an=2n-1,bn=n-1. 4分
∴Sn=(a1+a2+…+an)+(b1+b2+…+bn)
=(1+2+…+2n-1)+[0+1+…+(n-1)]
=2n-1+![]() . 6分
. 6分
(Ⅱ)Tn=![]() ≤
≤![]() ,因此存在满足条件的正整数M,
,因此存在满足条件的正整数M,
其中M的最小值是3. 9分
(Ⅲ)![]() Tn=
Tn=![]() (
(![]() )=
)=![]() . 12分
. 12分
20.(甲)解:由已知得S坐标为(0,0,6),B(2,2,0),C(-2,2,0).
M是SO的中点,M(0,0,3),G是△SBC的重心,
∴G(0,![]() ,2). 4分
,2). 4分
(Ⅰ)MG=![]() 6分
6分
(Ⅱ) ![]() =(0,
=(0,![]() ,-1),
,-1),![]() =(-2,-2,6).
=(-2,-2,6).
设(![]() ,
,![]() )=
)=![]() ,则cos
,则cos![]() =
=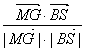
=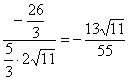 . 10分
. 10分
又∵![]() ∈(0°,90°),
∈(0°,90°),
∴![]() =arccos(
=arccos(![]() )或
)或![]() =
=![]() -arccos(-
-arccos(-![]() )即为MG与BS所成的角. 12分
)即为MG与BS所成的角. 12分
(乙)解:(Ⅰ)取AC中点E,连DE、BE,则DE∥PC,PC⊥AC,
∴DE⊥AC. 2分
又△ABC是正三角形,∴BE⊥AC,∴AC⊥平面DEB.
又BD![]() 平面BED,∴AC⊥BD. 5分
平面BED,∴AC⊥BD. 5分
(Ⅱ)由(Ⅰ)中知DE⊥AC,BE⊥AC,
∴∠DEB是二面角P—AC—B的平面角.
∴∠DEB=120°.又AB=2![]() ,其中线BE=
,其中线BE=![]() AB=3,DE=
AB=3,DE=![]() PC=1.
PC=1.
∵AC⊥平面BDE,
又AC![]() 平面ABC,
平面ABC,
∴平面ABC⊥平面BDE, 7分
且交线为BE,过D作平面ABC的垂线DF,垂足F必在直线BE上.
又∠DEB=120°,
∴设F在BE延长线上,则∠DBE即为BD与底面ABC所成的角. 9分
又△DEB中,DB2=DE2+BE2-2BE·DEcos120°=13,
∴BD=![]() .由正弦定理:
.由正弦定理:![]() ,
,
∴sinDBE=![]() ,即BD与底面ABC所成的角的正弦值为
,即BD与底面ABC所成的角的正弦值为![]() . 12分
. 12分
21.解:(Ⅰ)可设P1(x1,y1),P2(x2,y2) ,它们的中点P的坐标为(x,y),
则有x12-![]() =1,x22-
=1,x22-![]() =1, 2分
=1, 2分
两式相减得2(x1+x2)(x1-x2)=(y1+y2)(y1-y2), 3分
当x1≠x2时,y≠0 ,
由x1+x2=2x,y1+y2=2y,
得![]() . ①
. ①
又由P1、P2、P、A四点共线得:![]() , ②
, ②
由①②得![]() ,即2x2-y2-4x+y=0. 6分
,即2x2-y2-4x+y=0. 6分
当x1=x2 时,x=2,y=0满足此方程.
故线段P1P2的中点P的轨迹方程为2x2-y2-4x+y=0. 7分
(Ⅱ)假设满足题设条件的直线l′存在.可设Q1(x3,y3)、Q2(x3,y4) ,
同(Ⅰ)得2(x3+x4)(x3-x4)=(y3+y4)(y3-y4) , 9分
由x3+x4=2,y3+y4=2,得![]() =2(x3≠x4),
=2(x3≠x4),
即kl′=2,从而直线l′的方程为y-1=2(x-1),即 y=2x-1.
因为方程组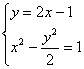 ,无解,矛盾. 11分
,无解,矛盾. 11分
故满足题设条件的直线l′不存在. 12分
22.解:(Ⅰ)由函数f(x)=x4-4x3+ax2-1,在区间[0,1)上单调递增,在区间[1,2)上单调递减,
∴x=1时,f(x)取得极大值,∴f′(1)=0. 2分
f′(x)=4x3-12x2+2ax,
∴4-12+2a=0![]() a=4. 4分
a=4. 4分
(Ⅱ)点A(x0,f(x0))关于x=1的对称点B坐标为(2-x0,f(x0)), 6分
f(2-x0)=(2-x0)4-4(2-x0)3+4(2-x0)2-1
=(2-x0)2[(2-x0)-2]2-1
=x04-4x03+4x02-1=f(x0). 8分
∴点A关于直线x=1的对称点B也在函数f(x)的图象上. 9分
(Ⅲ)函数g(x)=bx2-1的图象与函数f(x)的图象恰有3个交点,等价于方程x4-4x3+4x2-1=bx2-1恰有3个不等实根, 10分
x4-4x3+4x2-1=bx2-1![]() x4-4x3+(4-b)x2=0.
x4-4x3+(4-b)x2=0.
∵x=0是其中一个根,
∴方程x2-4x+(4-b)=0有两个非0不等实根. 12分
∴![]() ∴b>0且b≠4. 14分
∴b>0且b≠4. 14分