高考全国统一标准数学测试（文科B卷）
第Ⅰ卷(选择题 共60分)
一、选择题（本大题共12小题；每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）
1.定义在R上的函数y=f(x)的值域为［a,b］,则f(x+1)的值域为
A.［a,b］ B.［a+1,b+1］
C.［a－1,b－1］ D.无法确定
2.a=－1是直线ax+(2a－1)y+1=0和直线 3x+ay+3=0垂直的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.不充分也不必要条件
3.在等比数列｛an｝中，a1＞1,前n项和满足
Sn=
,那么a1的取值范围是
A.(1,+∞) B.(1,4)
C.(1,2) D.(1,
)
4.已知m、l是异面直线，那么：①必存在平面α过m且与l平行；②必存在平面β过m且与l垂直；③必存在平面γ与m、l都垂直；④必存在平面π与m、l距离都相等.其中正确的结论是
A.①② B.①③ C.②③ D.①④
5.10个人抽2张球票，一人一次依次抽取（每抽一次不放回），则第k个人抽到球票的概率（k=1,2,…,10）为
A.
B.
C.
D.
6.若得到函数y=sin(2x－
)的图象，可以把函数y=sin2x的图象
A.向左平移
个单位 B.向右平移个单位
C.向左平移个单位 D.向右平移个单位
7.设F1、F2是双曲线
－y2=1的两个焦点，点P在双曲线上，且
·
=0,则｜｜｜｜的值为
A.0 B.2 C.2 D.4
8.已知复数2－i的辐角主值是θ,则
+3i的辐角主值是
A.
－θ B.2π－θ
C.θ－π D.θ+
9.若双曲线以y=±
x为渐近线，F（0，2）为焦点，则此双曲线方程为
A.x2－
=1 B.x2－=－1
C.
=1 D.=－1
10.已知函数f(x)是R上的增函数，A(0,－1),B(3,1)是其图象上的两点，那么｜f(x+1)｜＜1的解集是
A.（1，4） B.（－1，2）
C.（－∞,1]∪［4,+∞) D.(－∞,－1]∪［2,+∞)
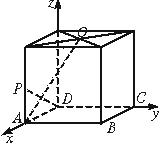
11.过正三棱锥S—ABC的一条侧棱SA及其外接球的球心O，作棱锥截面SAD.（如图）球心O在AD上，则此三棱锥的侧面三角形顶角的余弦值为
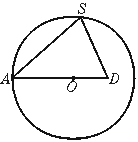
A.
B.0 C.－ D.
12.甲、乙两工厂2003年元月份的产值相等，甲厂的产值逐月增加，且每月增加的产值相同；乙厂产值也逐月增加，且每月增长的百分率相同.已知2004年元月份两厂的产值相等，那么2003年7月份产值高的工厂是
A.甲厂 B.乙厂
C.两厂产值一样 D.无法确定
第Ⅱ卷(非选择题 共90分)
二、填空题（本大题共4小题；每小题4分，共16分.把答案填在题中的横线上）
13.设f(x)=
,利用课本中推导等差数列前n项和公式的求法，可求得f(－5)+ f(－4)+f(－3)+…+f(4)+f(5)+f(6)的值为__________.
14.函数y=
在点x=3处的导数值为__________.
15.如下图，表示图中平面区域的公共区域的不等式组是__________.
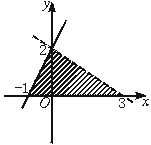
16.有一组数据：x1,x2,…xn（x1≤x2≤…≤xn）它们的算术平均值为10，若去掉其中最大的xn，余下数据的算术平均值为9；若去掉其中最小的x1,余下数据的算术平均值为11，则x1关于n的表达式为__________；xn关于n的表达式为__________.
三、解答题(本大题共6小题，共74分.解答过程应写出文字说明、证明过程或演算步骤)
17.（本小题满分12分）
设x∈［,
］,f(x)=(sin2x－cos2x－
)+sin2(x－),求f(x)的最大值和最小值.
18.（本小题满分12分）
有一个问题，在半小时之内，甲能解决它的概率是，乙能解决它的概率是
.
计算：（Ⅰ）两人都未解决的概率；
（Ⅱ）问题得到解决的概率.
19.（本小题满分12分）
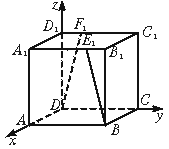
如图，在正方体ABCD－A1B1C1D1中，B1E1=D1F1=
.
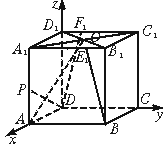
（Ⅰ）求BE1与DF1所成角的余弦值；
（Ⅱ）若A1C1∩B1D1=O，P为AA1上一点且DP⊥AD，求DP与底面ABCD所成角的正切值.
20.（本小题满分13分）
经市场调查分析知，某地明年从年初开始的前n个月，对某种商品需求总量f(n)（万件）近似地满足下列关系：f(n)=
n(n+1)(35－2n)(n=1,2,3,…，12).
（Ⅰ）写出明年第n个月这种商品需求量g(n)（万件）与月份n的函数关系式，并求出哪几个月的需求量超过1.4万件；
（Ⅱ）若计划每月该商品的市场投放量都是P万件，并且要保证每月都满足市场需求，则P至少为多少万件？
21.(本小题满分13分)
设椭圆
=1的内接三角形是△PAB，射线OP的倾斜角为，直线AP、BP的倾斜角互补.
（Ⅰ）求证：直线AB的斜率是定值；
（Ⅱ）求△PAB面积的最大值.
22.（本小题满分12分）
设数列{an}的首项a1=1，前n项和Sn满足关系式：3tSn－(2t+3)Sn－1=3t(t＞0,n=2,3,4,…).
（Ⅰ）求证：数列{an}是等比数列；
（Ⅱ）设数列{an}的公比为f(t)，作数列{bn}使b1=1,bn=f(
)(n=2,3,4,…).求bn;
（Ⅲ）求和：b1b2－b2b3+b3b4－b4b5+…+b2n－1b2n－b2nb2n+1.
参 考 答 案
一、1.A 2.A 3.D 4.D 5.B 6.B 7.B 8.C 9.B 10.B 11.D 12.A
二、13.3 14.－
15.
16.11－n n+9
三、17.（12分）解：f(x)= (－cos2x－)+
· 2分
=
－
sin2x－cos2x 4分
=－sin(2x+
). 6分
∵x∈［,］,∴(2x+)∈［
,
］. 8分
∴当x=时，f(x)min=－； 10分
当x=时，f(x)max=
. 12分
18.（12分）解：（1）设在半小时内甲能独立解决该问题是事件A，乙能独立解决该问题是事件B. 2分
那么两人都未解决该问题是事件
·
. 3分
由于两人是相互独立地求解，于是得到P（·）=P（）·P（）=（1－）（1－）=. 7分
（2）“问题得到解决”这一事件的概率为1－P（·）=1－=
. 12分
19.(12分)解：(Ⅰ)不妨设正方体的边长为1，建立空间直角坐标系O—xyz，如图，则 B（1，1，0）、E1（1，
，1）、D（0，0，0）、F1（0，，1）.
=（1，，1）－（1，1，0）=（0，－，1），
=（0，，1）－（0，0，0）=（0，，1）， 4分
=
，=，
·=0×0+(－×)+1×1=
,
∴cos＜,＞=
=
. 6分
（Ⅱ）设P点坐标为（1，0，z），
=（1，0，z）,O(,,1),A(1,0,0).
=(－,,1), 8分
∵DP⊥AO，
∴·=－+z=0.
z=,即AP=. 10分
∴DP与底面ABCD所成角为∠ADP，
则tanADP=. 12分
20.（13分）解：（Ⅰ）当n=1时，g(1)=f(1)=
. 2分
当n≥2时，g(n)=f(n)－f(n－1)=
(－n2+12n)(经检验n=1时也成立).
解不等式（－n2+12n）＞1.4, 5分
得5＜n＜7. 7分
∵n∈N,∴n=6,即第六个月的需求量超过1.4万件.
（Ⅱ）由题设可知，对于n=1,2,…,12恒有nP≥f(n),
即P≥ (n+1)(35－2n) 9分
=－［－2（n－
）2+
+35］ 11分
当且仅当n=8时，Pmin=
=1.14.
∴每月至少投放1.14万件. 13分
21.(13分)（Ⅰ）证明：OP的直线方程为y=x. 1分
联立方程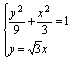
，得点P坐标为（
，
）.
设AP方程为y－=k(x－)，
BP方程为y－=－k(x－),
联立方程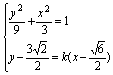
，得xA=
.
同理,得xB=
.
∴AB的斜率为kAB=
.
∴AB的斜率为定值.
（Ⅱ）解：设直线AB的方程为y=x+m，P点到直线AB的距离为d.
则d=
，将直线方程代入椭圆方程，得6x2+2mx+m2－9=0.
∴AB=2
.
S△ABP=dAB=
·
≤
.
当且仅当m=±3时，取等号,
∴(S△APB)max=. 13分
22.（12分）（Ⅰ）证明：∵3tSn－(2t+3)Sn－1=3t， ①
∴3tSn+1－(2t+3)Sn=3t. ② 1分
由②－①,得3t(Sn+1－Sn)－(2t+3)(Sn－Sn－1)=0. 2分
3tan+1=(2t+3)an.
∵
，又∵t＞0,a1=1＞0， 3分
∴an＞0,则{an}成等比数列. 4分
（Ⅱ)解：由（Ⅰ)知f(t)=
=
.
∴bn=f()=+bn－1，
bn－bn－1= (n≥2,n∈N*).
∴{bn}为等差数列且b1=1，公差d=.
则bn=1+ (n－1)=
. 8分
（Ⅲ）解：b1b2－b2b3+b3b4－b4b5+…+b2n－1b2n－b2nb2n+1
=b2(b1－b3)+b4(b3－b5)+…+b2n(b2n－1－b2n+1) 9分
=－2× (b2+b4+…+b2n)
（∵b2=
,b2n=
.） 10分
=－
11分
=－
n(2n+3). 12分