高考适应性考试数学(文史类)
一、选择题:(每小题5分,共60分)
1.若集合![]() ,且
,且![]() ,则集合M的元素最多只能有( )
,则集合M的元素最多只能有( )
A. 1个 B. 2个 C. 3个 D. 4个
2. 如果![]() ,且
,且![]() ,那么
,那么![]()
A.
![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
3.![]() 展开式中常数项为( )
展开式中常数项为( )
A 15 B 20 C 120 D 160
4.AD是等腰三角形ABC底边上的高,如果![]() 那么
那么![]() =( )
=( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
5.某电视台为调查节目收视率,想从全市5个市区中按人口数用分层抽样的方法抽取一个容量为![]() 的样本,已知5个区人口数之比为2:3:5:2:6,如果最多的一个区抽出的个体数是90,那么这个样本的容量
的样本,已知5个区人口数之比为2:3:5:2:6,如果最多的一个区抽出的个体数是90,那么这个样本的容量![]() 等于( )
等于( )
A 240 B 270 C 300 D 330
6.函数![]() 的反函数是______
的反函数是______
A ![]() B
B ![]() C
C ![]() D
D ![]()
7.已知函数![]() 当
当![]() 时,以下结论正确的是( )
时,以下结论正确的是( )
A.
![]() B.
B.
![]()
C.
![]() D.
D.
![]() .
.
8.![]()
![]() ,且直线
,且直线![]() ,直线
,直线![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.
![]() D.
D.
![]()
9.能够使得圆![]() 的圆心到直线
的圆心到直线![]() 的距离等于3的c的一个值为( )
的距离等于3的c的一个值为( )
A.
![]() B.
3
B.
3![]() C.
2 D.
3
C.
2 D.
3
10.“![]() >2”是“直线
>2”是“直线![]() 和直线
和直线![]() 垂直”的( )
垂直”的( )
A 充分而不必要条件 B 必要而不充分条件
 C 充分必要条件
D 既不充分也不必要条件
C 充分必要条件
D 既不充分也不必要条件
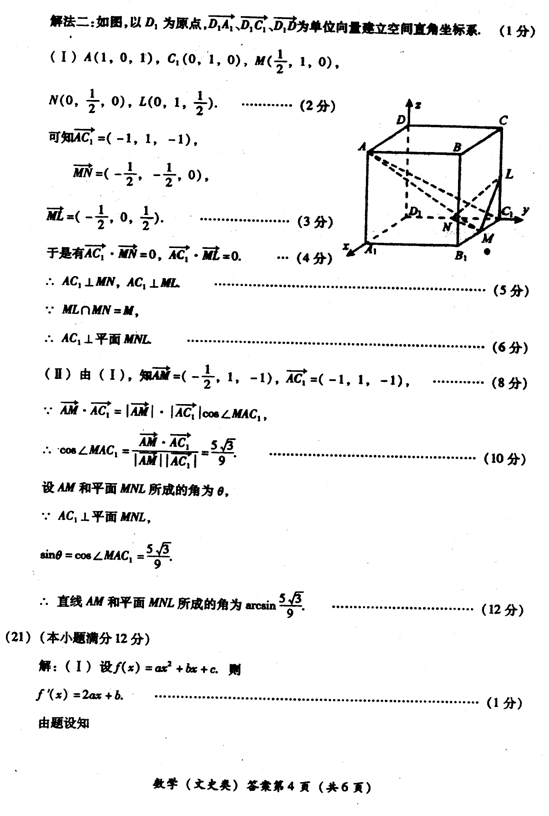
11.如图,F1、F2分别是椭圆![]() 的左、右焦点,P是以F1F2为
的左、右焦点,P是以F1F2为
直径的圆与该椭圆的一个交点,且![]() ,则这个椭圆的离
,则这个椭圆的离
心率是( )
A.
![]() B.
B. ![]() C.
C.![]() D.
D.
![]()
12.已知![]() 满足约束条件
满足约束条件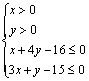 ,且
,且![]() 的最大值为( )
的最大值为( )
A. 16 B.19 C.20 D.31
二、填空题:(每小题4分,共16分)
13.A是抛物线![]() 上一点,如果点A的横坐标是3,且点A到抛物线焦点的距离是6,那么
上一点,如果点A的横坐标是3,且点A到抛物线焦点的距离是6,那么![]() =_____
=_____
14.若数列![]() 的前n项和为Sn,且
的前n项和为Sn,且![]() ,则该数列的通项公式
,则该数列的通项公式![]()
15.已知同一平面上不共线的三个向量![]() 两两所成的角均相等,且
两两所成的角均相等,且![]()
16.将边长为1的正方形纸片ABCD沿对角线AC翻折,使顶点B和D的距离为1,此时点D和平面ABC的距离为_______.
二、解答题:
17.(12分)设![]()
(1)求A、B、C的值;
(2)求![]() 最小值。
最小值。
18.(12分)甲、乙两名篮球运动员练习投篮,两人进球的概率分别为0.7与0.8。
(1)如果每人各投篮一次,求甲、乙两人至少有一人进球的概率;
(2)如果每人各投篮三次,求甲投进2球且乙投进1球的概率。
19.(12分)已知等比数列![]() 各项均为正数,且
各项均为正数,且![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)记数列![]() 的前n项和为
的前n项和为![]() ,证明
,证明![]()
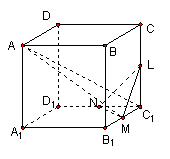
20.(12分)如图,ABCD -A1B1C1D1是棱长为1的正方体,点M、N、L分别是B1C1、D1C1、C1C三条棱的中点。
(1)求证:AC1⊥平面MNL;
(2)求AM和平面MNL所成的角。
21.(12分)已知二次函数![]() 当
当![]() 时有极值,函数图象过点
时有极值,函数图象过点![]() 点,且在该点处的切线与直线
点,且在该点处的切线与直线![]() 垂直。
垂直。
(1)求![]() 的解析式;
的解析式;
(2)若![]() 求
求![]() 的单调递减区间;
的单调递减区间;
22.(14分)已知动点P与双曲线![]() 的两个焦点F1、F2的距离之和为定值,且
的两个焦点F1、F2的距离之和为定值,且![]() 的最小值为
的最小值为![]()
(1)求动点P的轨迹方程;
(2)若已知点M、N在动点P的轨迹上,且对定点D(0,3),有![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。