法向量在高考数学中的应用
在全日制普通高级中学教科书—数学中,平面向量这一章的引言是:“向量是数学中的重要概念之一,向量和数一样也能进行运算,而且用向量的有关知识还能有效地解决数学,物理等学科中的许多问题”。从而引起对向量的重视。向量在研究几何问题中更显示出其优越性,为和国际数学接轨,在中学数学中增加了向量的有关知识,但是应用的还不充分。 特别是法向量在数量关系的求解中的应用没有得到应有的重视。作为一个导向,在以后的立体几何中将会加大法向量所占的比重。法向量的灵活应用,将使得原本很繁琐的推理,在利用法向量后变的思路清晰且规范。随着课程改革的进行,向量的应用将会更加广泛。这在2004年高考中教育部考试中心和实行分省命题所命制的高考数学试题中得到了充分的体现。
法向量在求角与距离中有以下几种应用。
1、法向量在求面面角中的应用:
原理:一个二面角的平面角![]() 1与这个二面角的两个半平面的法向量所成的角
1与这个二面角的两个半平面的法向量所成的角![]() 2相等或互补。
2相等或互补。
2、法向量在求线面角中的应用:
原理:设平面![]() 的斜线L与平面
的斜线L与平面![]() 所的角为
所的角为![]() 1,斜线L与平面
1,斜线L与平面![]() 的法向量所成角
的法向量所成角![]() 2,则
2,则![]() 1与
1与![]() 2互余或与
2互余或与![]() 2的补角互余。
2的补角互余。
3、法向量在求异面直线间的距离中应用:
原理:设分别以这两异面直线上任意两点为起点和终点的向量为![]() ,与这两条异面直线都垂直的向量为
,与这两条异面直线都垂直的向量为![]() ,则两异面直线间的距离是
,则两异面直线间的距离是![]() 在
在![]() 方向上的正射影向量的模。
方向上的正射影向量的模。
4、法向量在求点到平面的距离中的应用:
原理:设分别以平面外一点P与平面内一点M为起点和终点的向量为![]() ,平面的法向量为
,平面的法向量为![]() ,则P到平面的距离d等于
,则P到平面的距离d等于![]() 在
在![]() 方向上正射影向量的模。
方向上正射影向量的模。
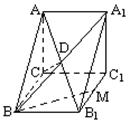
例1、(2004全国高考湖北省高考题)
如图,在棱长为1的正方体ABCD—A1B1C1D1中,AC与BD交于点E,CB与CB1交于点F.
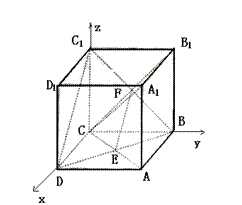 (I)求证:A1C⊥平BDC1;
(I)求证:A1C⊥平BDC1;
(II)求二面角B—EF—C的大小(结果用反三角函数值表示).
解析:(Ⅰ)以点C为坐标原点建立如图所示的空间直角坐标系,则C(0,0,0).
D(1,0,0),B(0,1,0),A1(1,1,1),C1(0,0,1),D1(1,0,1)
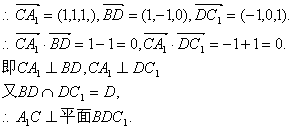
(Ⅱ)同(I)可证,BD1⊥平面AB1C.

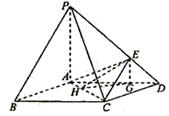
例2、(2004全国高考)
|
(Ⅰ)求证CD⊥平面BDM;
(Ⅱ)求面B1BD与面CBD所成二面角的大小.
解析:如图,以C为原点建立坐标系.
(Ⅰ)B(![]() ,0,0),B1(
,0,0),B1(![]() ,1,0),A1(0,1,1),
,1,0),A1(0,1,1),
D(![]() ,M(
,M(![]() ,1,0),
,1,0),
![]()
则![]() ∴CD⊥A1B,CD⊥DM.
∴CD⊥A1B,CD⊥DM.
因为A1B、DM为平面BDM内两条相交直线,所以CD⊥平面BDM.
(Ⅱ)设BD中点为G,连结B1G,则
G(![]() ),
),![]() 、
、![]() 、
、![]() ),
),![]()
![]()
![]()
所以所求的二面角等于![]()
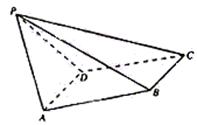
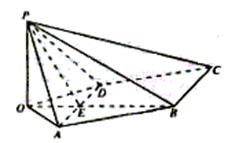
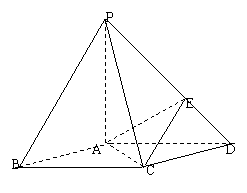 例3、(2004全国高考湖南卷)如图,在底面是菱形的四棱锥P—ABCD中,∠ABC=600,PA=AC=a,PB=PD=
例3、(2004全国高考湖南卷)如图,在底面是菱形的四棱锥P—ABCD中,∠ABC=600,PA=AC=a,PB=PD=![]() ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.
(I)证明PA⊥平面ABCD;
(II)求以AC为棱,EAC与DAC为面的二面角![]() 的大小;
的大小;
(Ⅲ)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论.
解析:证明 因为底面ABCD是菱形,∠ABC=60°,
|
由PA2+AB2=2a2=PB2 知PA⊥AB.
同理,PA⊥AD,所以PA⊥平面ABCD.
(Ⅱ)解 作EG//PA交AD于G,
由PA⊥平面ABCD.
知EG⊥平面ABCD.作GH⊥AC于H,连结EH,
则EH⊥AC,∠EHG即为二面角![]() 的平面角.
的平面角.
又PE : ED=2 : 1,所以![]()
从而 ![]()
![]()
(Ⅲ)解: 以A为坐标原点,直线AD、AP分别为y轴、z轴,过A点垂直平面PAD的直线为x轴,建立空间直角坐标系如图.由题设条件,相关各点的坐标分别为
|
![]()
所以 ![]()
![]()
![]()
设点F是棱PC上的点,![]() 则
则
![]()
![]() 令
令 ![]() 得
得
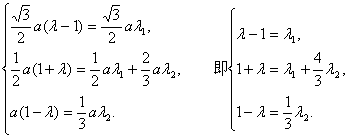
解得 ![]() 即
即 ![]() 时,
时,![]()
亦即,F是PC的中点时,![]() 、
、![]() 、
、![]() 共面.
共面.
又 BF![]() 平面AEC,所以当F是棱PC的中点时,BF//平面AEC.
平面AEC,所以当F是棱PC的中点时,BF//平面AEC.
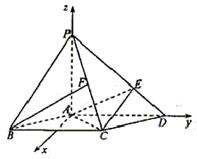
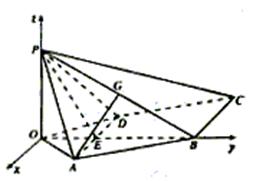
例4、 (2004全国高考河南,山西、山东等省高考题)
如图,已知四棱锥 P—ABCD,PB⊥AD侧面PAD为边长等于2的正三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120°.
|
(II)求面APB与面CPB所成二面角的大小.
解析: (I)解:如图,作PO⊥平面ABCD,垂足为点O.连结OB、OA、OD、OB与AD交于点E,连结PE.
|
∵PA=PD,∴OA=OD,
于是OB平分AD,点E为AD的中点,所以PE⊥AD.
由此知∠PEB为面PAD与面ABCD所成二面角的平面角,
∴∠PEB=120°,∠PEO=60°
由已知可求得PE=![]()
∴PO=PE·sin60°=![]() ,
,
即点P到平面ABCD的距离为![]() .
.
(II)解:如图建立直角坐标系,其中O为坐标原点,x轴平行于DA.
![]() .连结AG.
.连结AG.
|
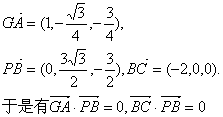
所以![]()
等于所求二面角的平面角,
于是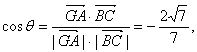
所以所求二面角的大小为![]() .
.