反函数
一、学习目标
1、了解反函数的概念;
2、掌握求一引起简单函数的反函数;
3、了解互为反函数的函数图像间的关系,能解决与反函数图像有关的简单问题;
4、培养用辩证的观念观察、分析、解决问题的能力;
5、培养探索、猜想、辨证的思维习惯。
二、例题分析
第一阶梯
[例1]![]()
分析:求反函数主要在于求解关于x的方程。
解:![]()
![]()
![]()
∵原来函数的值域就是反函数的定义域。
∴由原来函数的值域为
![]()
![]()
说明:
反函数的定义域是原来函数的值域,应先求原来函数的值域,然后得出反函数的定义域,一般情
况下,不能直接从求得的反函数的解析式中得出,例如y=x3(x≥1)的反函数为 ![]() ,定义域是
,定义域是
{xx≥1},而不是R。
[例2]![]()
分析:x的求解须先平方后开方。
解:![]()
![]()
![]()
![]()
由已知可求得原函数值域为0≤y≤5.
![]()
说明:![]()
第二阶梯
[例3]![]()
分析:
![]()
解:![]()
![]()
![]()
说明:解题时要注意条件的演变。
[例4]![]()
思路分析:
题中给出的函数的定义域有特定的限制,在求它的反函数时,要寻求使反函数存在的条件,进而
确定反函数的定义域和值域。
解答:![]()
![]()
![]()
第三阶梯
[例5]![]()
思路分析:根据反函数的概念求解。
解答:![]()
解得:![]()
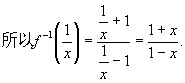
[例6]![]()
思路分析:![]()
解答:![]()
三、检测题
![]()
![]()
![]()
![]()
![]()
2.若函数y=f(x)的反函数是y=g(x),f(a)=b,ab≠0,则g(b)等于( )
A. a B. a-1 C. b D. b-1
3.若函数y=f(x)的图像经过点(1,0),则函数y=f-1(x)的图像必经过点( )
A. (0,-1) B. (1,0) C. (-1,0) D. (0,1)
4.函数y=ax+b与它的反函数是同一个函数,则系数a,b必满足条件( )
A. a=1, b=0 B. a=-1, b=0
C. a=±1,
b=0 D. a=1, b=0或a=-1,
b ![]() R
R
![]()
A. 2,1,3 B. -2,-1,-3 C. 3,-1,-2 D. -1,3,-2
6.如果f(x)的图像经过点(1,2),那么y=f-1(x)-1的图像必过点__________.
7.若函数f(x)的图像经过(0,1)点,则f(x+2)的反函数的图像恒经过点____________.
![]()
9.已知命题:
(1)若互为反函数的两个函数的图像有个交点,则交点必在直线y=x上;
(2)互为反函数的两个函数有相同的单调性;
(3)函数y=f(x)与函数x=f-1(y)的图像关于直线y=x对称;
(4)函数y=f(x)在单调区间必存在反函数。
其中,正确的命题有( )
A、1个 B、2个 C、3个 D、4个
10.若函数y=f(x)存在反函数,则方程f(x)=c(c为常数)( )
A、有且只有一个实根 B、至少有一个实根
C、至多有一个实根 D、没有实数根
11、设有三个函数,第一个函数是y=f(x),它的反函数是第二个函数,而第三个函数与第二个函数的
图像关于原点对称,那么第三个函数是( )
A. y=-f(x) B. y=f-1(-x) C. y=-f-1(-x) D. y=f-1(x)
12.函数y=f(x)的图像经过第三、四象限,则y=-f-1(x)的图像经过( )
A、第一、二象限 B、第二、三象限
C、第三、四象限 D、第一、四象限
13.函数f(x)=ax3+ax-1的反函数的图像必过点____________________.
14.已知函数f(x)是定义在R上单调递增的奇函数,又f-1(1+a)+f-1(1-a2)<0,试求a的取值范围。
15.若f(x-1)=x2-2x+3(x≤0),求f-1(x)。
答案:
1—5 B A D D B
6、(2,0)
7、(1,-2)
8、-1
9、B
10、C
11、C
12、B
13、(-1,0)
14、 a<-1或a>2.
15、解:f(x-1)=(x-1)2+2,
∵f(x)=x2+2(x≤-1),
![]()