第四节数列求和
【例1】已知
是数列
的前
项和，且
，求
【例2】已知数列的通项
是关于
的不等式
的解集中整数的个数。
（1）求数列的通项；
（2）设
，求数列
的前项和。
【例3】在数列中，
，是它的前项的和，且
）
（1）求和；
（2）求证：
【例4】设数列的首项
，前项和满足关系式：
（1）求证：数列是等比数列；
（2）设数列的公比为
，作数列，使
，求数列的通项
；
（3）求和：
。
双基训练
1、数列
，…，
的前项和是__________________
2、数列9，99，999，…的前项和是______________
3、数列的通项公式是
，则它的前51项和是_______________
4、数列
，
，3×
，…，×
，…，的前项和是_______________--
5、设是等差数列的前项和，又
，则＝______
6、数列
，
，
，…，
，…的前项和为_______
7、设
，那么和式：
=_______
8、已知数列的通项公式是
，求此数列的前项和
9、数列的前项和和满足
，求和
10、求和：
知识升华
1、设
，则数列
，
，…，
，…，的前项和为_______________
2、等比数列的公比是负数，则由前项和组成的数列
是个（ ）
A、减数列 B、增数列 C、摆动数列 D、先增后减数列
3、数列的通项公式是
，若前项和为10，则项数＝_____
4、
…+
＝_______
5、已知数列中，
，且
，则
＝______
6、设
…+
，则
______
7、设为等比数列，为等差数列，且
，
，若数列
是1，1，2，…，则的前10项和为___________________
8、定义“等和数列”：在一个数列中，如果每一项与它的后一项的和都为同一个常数，那么这个数列叫做等和数列，这个常数叫做该数列的公和。已知数列是等和数列，且，公和为5，那么
＝___________,这个数列前项和的计算公式为_____________
9、已知数列中，，
且
，则
＝______
10、已知正数数列的前项和为，且有
…+
，求与
11、求和：
…+
12、一个数列，当为奇数时，
，求这个数列前
项的和（
是正整数）
挑战高考
1、把数列
依次按第一个括号一个数，第二个括号两个数，第三个括号三个数，第四个括号四个数，第五个括号一个数，…，循环分为：（3），（5，7），（9，11，13），（15，17，19，21），（23），（25，27），（29，31，33），（35，37，39，41），（43），…，则第104个括号内各数之和为__________
2、已知数列的前项和
…），其中
是非零常数，则存在数列
，
使得（ ）
A、
，其中为等差数列，为等比数列；
B、，其中和都为等差数列
C、，其中为等差数列，为等比数列
D、，其中和都为等比数列
3、给出数阵：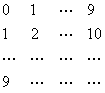
其中每行、每列均为等差数列，则此数阵中所有数的和为_____
4、已知数列、都是等差数列，
，且
分别表示数列、的前
项和
，若
，又有
，求数列
的前项和；欲使此和大于2004，正整数至少取何值？
5、若
，则
＝__________
6、设数列是数列的前项和，满足
且
，
。数列满足
（Ⅰ）求数列的通项公式；
（Ⅱ）若数列中每一项总小于它后面的项，求
的取值范围。
7、设函数
的定义域为R，当
时，
，且对任意的实数
,有
（1）求
，判断并证明函数
的单调性；
（2）数列满足
，且
①求通项公式的表达式；
②令
，
…+，
…+
，试比较欲
的大小，并加以证明。
8、已知数列中，，其前项和为，且
，当
时，
。
（1）求数列的通项公式；
（2）若
，求数列的前项和。
9、数列的前项和为，且
（1）若一等差数列恰使数列
是以
为公比的等比数列，求通项；
（2）求。
10、设函数
，已知不论
为何实数时，恒有
，
，对于正数数列，其前项和
（Ⅰ）求
的值；
（Ⅱ）求数列的通项公式；
（Ⅲ）是否存在等比数列，使得
…+
对于一切正整数都成立，并证明你的结论。
（Ⅳ）若
，且数列
的前项和为
，试比较与
的大小。并予以证明。
11、已知等差数列中，公差
，其前项和为，且满足
，
。
（Ⅰ）求数列的通项公式；
（Ⅱ）通过公式
构造一个新的数列，若也是等差数列，求非零常数
。
（Ⅲ）求
的最大值。