第四节线段的定比分点与平移
【例1】已知A、B、C三点共线，且点B分有向线段
所成的比是3，求：
（1）点A分有向线段
所成的比
；
（2）点C分有向线段
所成的比
。
【例2】已知
，连结A、B并延长至P，使
，求P点坐标。
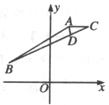【例3】如图所示，已知点
，求△ABC中
∠A的平分线AD的长。
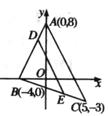【例4】已知三角形的三个顶点坐标为
，D点内分的比为1：3，E在BC上，且使△BDE的面积是△ABC面积的一半，求E点坐标。
【例5】已知两个点
和向量a =
，回答下列问题：
（1）把点P按向量a平移，求其对应点的坐标；
（2）某一点按向量a平移，得到的对应点是P/，求这个点的坐标；
（3）点P按某一向量平移，得到的对应点是P/，求这个向量的坐标。
【例6】已知抛物线
按a平移后，使得抛物线的顶点在y轴上，且在x轴上截得的弦长为4，求平移后的抛物线的方程及a
【例7】将函数
进行平移，使得到的图象与抛物线
的两个交点关于原点对称，求平移后的函数解析式。
【例8】设函数
a·b，其中向量a=
b=
（1）若
，且
，求x；
（2）若函数
的图象按向量
平移后得到函数
的图象，求实数m、n的值。
【例9】运用平移变换化简函数
为
的形式，并写出函数的单调区间。
【例10】是否存在这样的一个平移，使抛物线
平移后过原点，且以平移后的抛物线的顶点和它与
轴的两个交点为顶点的三角形的面积为1，若不存在，请说明理由；若存在，求出平移后的函数解析式。
双基训练
1、已知A、B、C三点共线，且A、B、C三点的纵坐标分别为2、5、10，则点A分所成的比是（ ）
A、
B、
C、
D、
2、设
是两个相异的点，点
的坐标由公式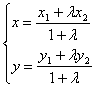
确定，则当
时，点C可表示（ ）
A、直线AB上的所有点
B、直线AB上除去点B的所有点
C、直线AB上除去点A的所有点
D、直线AB上除去点A、B的所有点
3、已知三个点
，点C在
上，且
，连结DC并延长至E，使
，则E点的坐标是（ ）
A、（0，1） B、
C、
或
D、
4、已知△ABC的顶点
和重心
，则BC边上的中点坐标是（ ）
A、
B、
C、
D、
5、把函数
的图象，按向量a=
平移后，图象的解析式是（ ）
A、
B、
C、
D、
6、设
和
两点，若点P在直线OA上，且
，P是线段OB的中点，则B的坐标是 。
7、已知点
，若直线l：
与直线MN相交于点P，
则
。
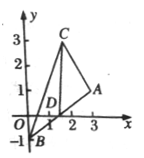8、如图，△ABC的顶点
，重心
（1）求
；
（2）若D为AB的中点，求中线CD的长。
9、已知点
，若直线l /：
与直线AB相交，求
的取值范围。
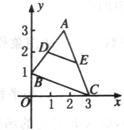10、如图，已知
，点D、E分别在AB、AC
上，DE∥BC，且DE平分△ABC的面积，求点D的坐标。
知识升华
1、点
按a平移至
，则
的图象按a平移后的图象的函数表达式为（ ）
A、
B、
C、
D、
2、函数
的图象按a=
平移，得到的图象的函数表达式为（ ）
A、
B、
C、 
D、
3、若把一个函数图象按a=
平移后得到函数
的图象，则原图象的函数解析式为（ ）
A、
B、
C、
D、
4、若曲线是由曲线按向量
平移得到的，那么是（ ）
A、
B、
C、
D、
5、将曲线上的点
平移变为
，平移后曲线的新解析式为（ ）
A、
B、
C、
D、
6、将的图象先平移，再作关于直线
的对称图象，所得图象的解析式为
，则这个平移为（ ）
A、向左平移1个单位 B、向右平移1个单位
C、向上平移1个单位 D、向下平移1个单位
7、如果直线l沿轴负方向平移了3个单位，再沿
轴正方向平移1个单位后，又回到原来的位置，那么直线的l斜率为（ ）
A、
B、
C、
D、3
8、把一个函数的图象按向量a =
平移后得到的图象的解析式为
，则原来函数的解析式是 。
9、已知
按向量
平衡到
，则
。
10、连接直角三角形的直角顶点与斜边的两个三等分点，所得两条线段的长分别为
和
，求斜边的长。
11、设函数
，试根据函数
的图象作出
的图象，并写出变换
过程。
12、已知
的图象F按a =
平移得到F /，已知
在F /上，F与F /的交点是
，试求F对应的函数解析式。
挑战高考
1、若将函数的图象按向量a平移，使图象上点的坐标由
变为
，则平移后的图象的解析式为（ ）
A、
B、
C、
D、
2、将函数
按向量a =
平移后的函数解析式为（ ）
A、
B、
C、
D、
3、将抛物
沿向量a平移得到抛物线
，则向量a为（ ）
A、
B、
C、
D、
4、将函数
的图象按向量a=
平移，得到函数
的图象，那么函数可以是（ ）
A、
B、
C、
D、
5、一函数图象沿向量a=
平移后，得到函数
的图象，则原函数在
上的最大值为（ ）
A、3 B、
6、已知抛物线
按a平移，使顶点在直线
上，且在轴上截得的弦长为6，则a = 。
7、把函数
的图象按向量a平移后，得到的图象，且a⊥b，
c =
，b·c = 4，则b = 。
8、甲船由A岛出发向北偏东45°的方向作匀速直线航行，速度为15
海里/小时，在甲船从A岛出发的同时，乙船从A鸟正南40海里外的B 岛出发，朝北偏东
的方向作匀速直线航行，速度为
海里/小时。（如图所示）。
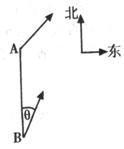（1）求出发后3小时两船相距多少海里？
（2）求两船出发后多长时间相距最近？最近距离为多少海里？