第四章复数

第四章　复　数

目录：

一．本章知识结构

二．学习内容和要求

（一）学习目标

（二）本章知识精要

三．学习方法与指导

（一）学习方法点拨

（二）典型例题讲解

1．复数的概念

2．复数的四则运算

（三）单元检测

（四）参考答案

四．2004年部分高考题回顾

一．本章知识结构

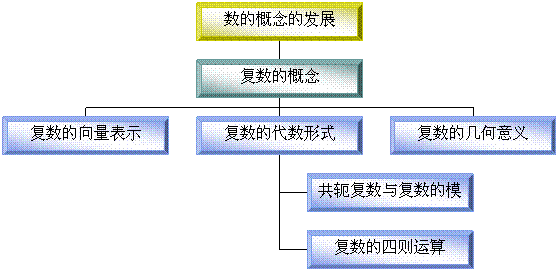
二．学习内容和要求

（一）学习目标

1．了解引进复数的必要性，数集的扩展过程及复数的分类表；

2．理解复数的有关概念；

3．掌握复数的代数形式；

4．掌握复数的代数形式的运算法则；

5．能进行复数的加、减、乘、除运算；

6．掌握某些特殊复数的运算特征

7．能在复数集中因式分解、解一元二次方程等。

（二）本章知识精要

1．复数的概念：

（1）虚数单位i；

（2）复数的代数形式z=a+bi，(a, b∈R)；

（3）复数的实部、虚部、虚数与纯虚数。

2．复数集

　　

3．复数的四则运算

　　若两个复数z₁=a₁+b₁i，z₂=a₂+b₂i，

（1）加法：z₁+z₂=(a₁+a₂)+(b₁+b₂)i；

（2）减法：z₁－z₂=(a₁－a₂)+(b₁－b₂)i；

（3）乘法：z₁·z₂=(a₁a₂－b₁b₂)+(a₁b₂+a₂b₁)i；

（4）除法：；

（5）四则运算的交换率、结合率；分配率都适合于复数的情况。

（6）特殊复数的运算：

① (n为整数)的周期性运算；　② (1±i)²=±2i；

③ 若ω=－+i，则ω³=1，1+ω+ω²=0.

4．共轭复数与复数的模

（1）若z=a+bi，则，为实数，为纯虚数(b≠0).

（2）复数z=a+bi的模，a=, 且=a²+b².

三．学习方法与指导

（一）学习方法点拨：

1．数的概念是从实践中产生和发展起来的。随着生产和科学的发展，书的概念也不断的被扩大和充实，从自然数集、整数集、有理数集到实数集的每一次扩充，推动了生产的进一步发展，也使数的理论逐步深化和发展，复数最初是由于解方程得需要产生的，后来由于在科学技术中得到应用而进一步发展。

要求熟悉我们已经学过的各种数集之间的内在联系。理解复数在其中所起到的重要作用，和各种数集之间的包含关系，即.

2．复数a+bi(a, b∈R)由两部分组成，实数a与b分别称为复数a+bi的实部与虚部，1与i分别是实数单位和虚数单位，当b=0时，a+bi就是实数，当b≠0时，a+bi是虚数，其中a=0且b≠0时称为纯虚数。

应特别注意，a=0仅是复数a+bi为纯虚数的必要条件，若a=b=0，则a+bi=0是实数。

3．根据两个复数相等的定义，设a, b, c, d∈R，两个复数a+bi和c+di相等规定为a+bi=c+di. 由这个定义得到a+bi=0.

两个复数不能比较大小，只能由定义判断它们相等或不相等。

两个复数相当的定义实际上给出了将复数问题转化为实数问题的方法，是求复数值、在复数集中解方程得重要依据。

4．复数a+bi的共轭复数是a－bi，若两复数是共轭复数，则它们所表示的点关于实轴对称。若b=0，则实数a与实数a共轭，表示点落在实轴上。

5．复数的加法、减法、乘法运算与实数的运算基本上没有区别，最主要的是在运算中将i²=－1结合到实际运算过程中去。

如(a+bi)(a－bi)=a²－(bi)²=a²－b²i²=a²+b².

6．复数的除法是复数乘法的逆运算将满足(c+di)(x+yi)=a+bi (c+bi≠0)的复数x+yi叫做复数a+bi除以复数c+di的商。

由于两个共轭复数的积是实数，因此复数的除法可以通过将分母实化得到，即.

7．复数a+bi的模的几何意义是指表示复数a+bi的点到原点的距离。

（二）典型例题讲解

1．复数的概念

例1．实数m取什么数值时，复数z=m+1+(m－1)i是（1）实数？（2）虚数？（3）纯虚数？（4）对应的点Z在第三象限？

解：复数z=m+1+(m－1)i中，因为m∈R，所以m+1，m－1都是实数，它们分别是z的实部和虚部，

∴ （1）m=1时，z是实数；　（2）m≠1时，z是虚数；

（3）当时，即m=－1时，z是纯虚数；

（4）当时，即m<－1时，z对应的点Z在第三象限。

例2．已知(2x－1)+i=y－(3－y)i，其中x, y∈R，求x, y.

解：根据复数相等的意义，得方程组，得x=, y=4.

例3．已知x与y实部相等，虚部互为相反数，且(x+y)²－3xyi=4－6i，求x, y.

解：由题意设x=a+bi，y=a－bi (a, b∈R)，则代入原式得

(2a)²－3(a²+b²)i=4－bi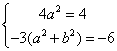，或或或，∴ 或或或.

例4．当m为何实数时，复数z＝+(m²+3m－10)i；（1）是实数；（2）是虚数；（3）是纯虚数．

　　解：此题主要考查复数的有关概念及方程（组）的解法．

　　（1）z为实数，则虚部m²+3m－10=0，即，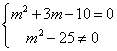

解得m=2，∴ m=2时，z为实数。

（2）z为虚数，则虚部m²+3m－10≠0，即，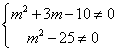

解得m≠2且m≠±5. 当m≠2且m≠±5时，z为虚数．，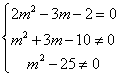

解得m=－, ∴当m=－时，z为纯虚数．

　　诠释：本题应抓住复数分别为实数、虚数、纯虚数时相应必须具备的条件，还应特别注意分母不为零这一要求．

例5．计算：i＋i²＋i³+……+i²⁰⁰⁵.

　　解：此题主要考查iⁿ的周期性．

i＋i²＋i³+……+i²⁰⁰⁵=(i+i²+i³+i⁴)+……+(i²⁰⁰¹+i²⁰⁰²+ i²⁰⁰³＋i²⁰⁰⁴)＋i²⁰⁰⁵

　 =(i－1－i+1)+ (i－1－i+1)+……+(i－1－i+1)+i

　　＝0＋0＋……＋0+i＝i.

　　或者可利用等比数列的求和公式来求解（略）

　　诠释：本题应抓住iⁿ的周期及合理分组．

例6．当θ为何值时，z₁＝z₂，其中：z₁＝1＋sinθ－icosθ，z₂=.

解：此题主要考查复数相等的充要条件及有关三角函数的知识．

∵ z₁＝z₂, ∴ 1＋sinθ－icosθ=, 即

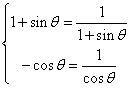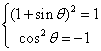，∴ ，∴ 无解，即θ不存在。

诠释：本题应抓住复数相等的充要条件．

例7．已知x、y、t∈R，t≠－1且 t≠0，求满足x＋yi=时，点(x, y)的轨迹方程。

解：此题主要考查复数相等的充要条件，轨迹方程的求法．

∵ x＋yi=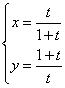，∴ ， ∴xy=1,

∴ 点(x，y)的轨迹方程为xy＝1，它是以x轴、y轴为对称轴，中心在(0，0)的等轴双曲线．

诠释：本题应抓住复数相等的充要条件及消参数来求点的轨迹方程。

例8．使不等式m²－(m²－3m)i＜(m²－4m＋3)i＋10成立的实数m＝　　　　　　 .

解：此题主要考查复数能比较大小的条件及方程组和不等式的解法．

∵ m²－(m²－3m)i＜(m²－4m＋3)i＋10, 且虚数不能比较大小，

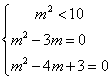∴，解得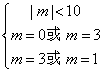，∴ m=3.

当m＝3时，原不等式成立．

诠释：本题应抓住复数能比较大小时必须都为实数这一条件。

例9．已知z=x＋yi(x，y∈R)，且 ，求z．

解：本题主要考查复数相等的充要条件及指数方程，对数方程的解法．

∵ ，∴，∴，

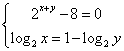解得或, ∴ z＝2＋i或z＝1＋2i．

诠释：本题应抓住复数相等的充要条件这一关键，正确、熟练地解方程（指数，对数方程）

例10．已知x为纯虚数，y是实数，且2x－1＋i＝y－(3－y)i，求x、y的值．

解：本题主要考查复数的有关概念，实数与i的运算，复数相等的充要条件，方程组的解法．

设x＝ti (t∈R，且t≠0），则2x－1＋i＝y－(3－y)i可化为

2ti－1＋i＝y－(3－y)i，即(2t＋1)i－1=y－(3－y)i，

∴, ∴y=－1, t=－, ∴ x=－i.

2．复数的四则运算

例1．计算：

（1），n∈N⁺；　

（2）若ω=－+i，ω³=1，计算；

（3）；

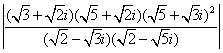（4）S=1+2i+3i²+4i³+……+100i⁹⁹.

解：（1）=

　　　　　　　　  =.

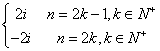（2）=

　　　　　　　　　　　 =－2.

（3）由于, ,

∴ =

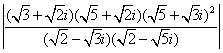　　　　　　　　　　　　　　　 =8.

（4）S=1+2i+3i²+4i³+……+100i⁹⁹

=(1+2i+3i²+4i³)+(5i⁴+6i⁵+7i⁶+8i⁷)+……+(97i⁹⁶+98i⁹⁷+99i⁹⁸+100i⁹⁹)

=(1+2i－3－4i)+(5+6i－7－8i)+……+(97+98i－99－100i)

=25(－2－2i)=－50－50i.

例2．已知复数z满足z－2=2，z+∈R，求z.

解：设z=x+yi, x, y∈R，则

z+=z+，

∵ z+∈R，∴ =0， 又z－2=2, ∴ (x－2)²+y²=4,

联立解得，当y=0时, x=4或x=0 (舍去x=0, 因此时z=0)，

当y≠0时, 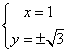, z=1±,

∴ 综上所得 z₁=4，z₂=1+i，z₃=1－i.

例3．设z为虚数，求证：z+为实数的充要条件是z=1.

证明：设z=a+bi (a, b∈R，b≠0)，于是

z+=(a+bi)+,

所以b≠0, (z+)∈Rb－=0a²+b²=1z=1.

例4．复数z满足(z+1)(+1)=²，且为纯虚数，求z.

解：设z=x+yi (x, y∈R)，则

(z+1)(+1)=²+z++1=²，∴ z++1=0，z+=－1，x=－.

==为纯虚数，

∴　x²+y²－1=0, y=±, ∴ z=－+i或z=－－i.

例5．复数z满足(1+2i)z+(3－10i)=4－34i，求z.

解：设z=x+yi (x, y∈R)，则(1+2i)(x+yi)+(3－10i)(x－yi) =4－34i，

整理得(4x－12y)－(8x+2y)i=4－34i.

∴ , 解得, ∴ z=4+i.

例6．设z是虚数，ω=z+是实数，且－1<ω<2，

（1）求z的值及z的实部的取值范围；（2）设u=，求证u为 纯虚数；

（3）求ω－u²的最小值。

解：（1）设z=a+bi (a, b∈R, b≠0)，则

ω=，由于ω是实数且b≠0，∴ a²+b²=1，

即z=1，由ω=2a, －1<ω<2, ∴ z的实部a的的取值范围是(－, 1).

（2）u==，由于a∈(－, 1), b≠0，

∴ u是纯虚数。

（3）ω－u²=2a+

　　　　  =,

由于a∈(－, 1)，∴ a+1>0，则ω－u²≥2×2－3=1，

当a+1=, 即a=0时，上式取等号，所以ω－u²的最小值为1.

例7．证明：＝1．

　　解：此题考查复数的运算、模的定义，共轭复数的性质等．

　　设z＝a＋bi，(a, b∈R)，则

　　=.

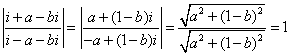　　解2：∵ ，∴ =.

诠释：此题抓住模的定义或共轭复数的性质来求解．

例8．(2002年高考)已知复数z＝1＋i，求实数a，b使az+2b＝(a＋2z)²．

　　解：此题主要考查共轭复数，复数的四则运算，复数的相等．

　　∵ z＝1＋i，∴az+2b＝(a＋2b)＋(a－2b)i，

　　(a＋2z)²＝(a＋2)²－4＋4(a＋2)i=(a²＋4a)＋4(a＋2)i．

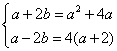∴ ，解得.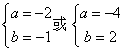

例9．若复数z满足z=(t∈R)，求z的对应点Z的轨迹方程．

　　解：此题主要考查复数的四则运算，点的轨迹方程的求法等．

　　设z＝x＋yi，(x, y∈R)，∵ z==，

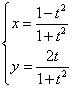∴ ，消去参数 t，得x²＋y²= 1，且x≠－1．

　　∴ 所求方程为x²＋y²＝1（x≠－1）．

　　诠释：解此题应抓住复数相等的充要条件，从而得到参数方程，消去参数，或者利用模的定义和性质，求出z即可．

例10．已知复数z满足z＝5，且(3+ 4i)z是纯虚数，求z．

　　解：此题主要考查复数的有关概念，复数的运算，模的定义及计算．

　　设 z＝x＋yi（x, y∈R）,　∵z＝5，

∴x²＋y²＝25,　又(3＋4i)z=(3＋4i)(x＋yi)＝(3x－4y)+(4x＋3y)i是纯虚数，

∴ ，　 联立三个关系式解得，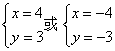

　　∴ z=4＋3i或z＝－4－3i．

诠释：解此题应抓住纯虚数的定义和模的定义而得到方程组，正确解方程组即可．

例11．设是纯虚数，求复数z对应的点的轨迹方程．

　　解：此题主要考查复数的有关概念及性质，四则运算和点的轨迹方程的求法．

∵ 是纯虚数，∴ ，即,

∴ ，∴ 2z+z+=0，(z≠0，z≠－1)，

　　设z=x＋yi，(x，y∈R)，2(x²＋y²)＋2x＝0（y≠0）

∴ (x＋)²＋y²＝（y≠0）．它为复数z对应点的轨迹方程．

　　诠释：解此题应抓住虚数的定义和共扼复数的性质，利用运算法则进行求解。

（三）单元检测

一、选择题：

1．设f(a)=(n∈N)，则集合{f(n)}中元素的个数为（　）

　　A．4　　　B．3　　　 C．2　　　 D．1

2．已知等比数列的第100项为2i，第300项为－200i，则它的第200项为（　）

　A．20　　 B．± 20　　　C．－198i　　　　D． 202i

3．设条件甲：x=0，条件乙：x＋yi（x，y∈R）是纯虚数，则（　）

　　A．甲是乙的充分非必要条件　　 B．甲是乙的必要非充分条件

　C．甲是乙的充分必要条件　　　 D．甲是乙的既不充分，又不必要条件

4．已知关于x的方程x²－(2i－1)x＋3m－i＝0有实根，则实数m应取的值是（　）

　A．m≥－　　  B．m≤－　　C．m=　　  D．m=－

5．有下列命题： ① 若z∈C，则z²≥0；② 若z₁，z₂∈C，z₁－z₂>0，则z₁>z₂；

③ 若a>b，则a＋i>b＋i．其中，正确命题的个数为（　）

　A．3　　　 B．2　　　 C．1　　　D．0

6．设R⁺，R^—，M分别表示正实数集，负实数集，纯虚数集，则集合加{m² m∈M}是（　）

　A．R⁺　　　B．R^－　　 C．R⁺∪R^－　　　　D．R^－∪{0}

7．等于（　）

　　A．0　　　 B．1　　　C．－1　　　D．i

8．设f(z)＝1+z－，若f(－)＝10－3i，则z等于（　）

　　A．5＋3i　　B．5－3i　　C．－5＋3i　　 D．－5－3i

9．方程x²＋(k+2i)x＋2＋ki＝0至少有一实根的条件是（　）

　A．－2≤k≤2　　  B．k≤－2或k≥2

　C．k=±2　　　　　 　 D．k≠2

10．若2＋3i是方程x²+mx+n＝0的一个根，则实数m，n的值为（　）

　　A．m＝4，n=－3　　　　B．m=－4，n＝13

　　C．m＝4，n=－21　　　 D．m=－4，n＝－5

11．在复平面上，复数z所对应的点在二、四象限的角平分线上，则z²所对应点的轨迹是（　）

　A．y轴　　B．y轴正半轴　　 C．y轴负半轴　　　D．x轴

二、填空题：

12．计算：i²⁹+i³⁰+ i³¹＋i³²+……＋i²⁵⁰＝　　　　　　　  .

13．设m∈R，z＝(2＋i)m²－3(1＋i)m－2(1－i)，当m=　　　　  时，z∈R；当m=　　　　　 时，z为纯虚数．

14．已知下列命题：

　　（1）在复平面中，x轴是实轴，y轴是虚轴；

　　（2）任何两个复数不能比较大小；

　　（3）任何数的偶次幂都是非负数；

　　（4）若 t＋si=3－4i，则 t=3、s=－4．

　　其中真命题为　　　　　　  　　．

15．若复数z满足z+=－1＋2i，则z=　　　　　　　　 .

16．设z∈C，z=1，则z++i的最大值为　　　　　  .

三、解答题：

17．设z=(a²－a－b)+，试判断复数z能否为纯虚数？并说明理由．

18．关于x的方程a(1+ i)x²+(1+a²i)x+a²＋i=0 (a∈R）有实根，求a的值及方程的根．

19．已知关于t的一元二次方程 t²＋(2＋i)t＋2xy＋(x－y)i=0（x、y∈R），当方程有实根时，求点(x，y)的轨迹方程．

20．已知复数z满足z＝1＋3i－z．求的值．

21．已知z=(a>0)，复数ω=z(z+i)，Re(ω)－Im(ω)=－，求ω．

22．若z∈C，满足4z＋2＝3+i，ω=sinθ－icosθ．求z的值和z－ω的取值范围。

（四）参考答案

一．选择题：

题号	1	2	3	4	5	6	7	8	9	10	11
答案	B	B	B	C	D	B	A	B	C	B	C

二．填空题：

12．i－1　　　　　  13．m=2或1；m=－　　　　　  14．①

15．－+2i　　　　 16．3

三．解答题：

四．2004年部分高考试题回顾

1．(福建1)复数的值是（ A ）

　　　 A．－1　　　　　　 B．1　　　　　　　　 C．－32　　　　　 D．32

2．(湖北2)复数的值是(  A ）

　　　 A．－16　　　　　　　　 B．16　　　　　　　　　　 C．　　　　　　　　　　D．

3．(湖南1)复数的值是（ D ）

　　　 A．　　　　　　　　　　 B．－　　　　　　　　 C．4　　　　　　　　　　　 D．－4

4．(辽宁4)设复数z满足（ C ）

　　　 A．0　　　　　　　　　　　 B．1　　　　　　　　　　　 C．　　　　　　　　　 D．2

5．(全国一．1) (1－i)²·i=（ D ）

　　　 A．2－2i　　　　　　　　B．2+2i　　　　　　　　　C．－2　　　　　　　　　 D．2

6．(全国二．3)设复数=（ C ）

　　　 A．　　　　　　　　　B．　　　　　　　　　　C．　　　　　　　　 D．

7．(全国三．6)设复数的辐角的主值为，虚部为，则=（ A ）

　　　A．　 　 B．　　C．　 　　　 D．

8．(天津1) i是虚数单位，=（ D ）

　　　 A． 　　B． 　　C． 　　D．

9．(重庆2)设复数, 则（ A ）

　　　A．–3　　　　 　　 B．3　　　　  　C．－3i　　　　 D．3i

10．(广东14)已知复数z与 (z +2)²－8i 均是纯虚数，则 z = 　　－2i　　　  .

11．（上海17）(本题满分12分)

已知复数z₁满足(1+i)z­₁=－1+5i, z­₂=a－2－i, 其中i为虚数单位,a∈R, 若<,求a的取值范围.

解：由题意得 z₁==2+3i,

　于是==,=.

　<,得a²－8a+7<0,1<a<7.