第五节数列的应用
【例1】用分期付款的方式购买一批总价为2300万元的住房,购买当天首付300万元,以后每月的这一天都交100万元,并加付此前欠款的利息,设月利息为1%,若首付300万元之后的第一个月开始算分期付款的第一个月,问分期付款的第10个月应付多少万元?全部贷款付清后,买这批住房实际支付多少万元?
【例2】某房地产开发商采用分期付款方式向社会出售商品住房,具体事宜如下:
(1)每套商品住房售价为400000元;
(2)购房者必须在一年内将款全部付清;
(3)购房者可分3次或4次付款;月利率为5%,每月利息按复利计算。
计算分4次付款购买1套商品住房:每期应付款多少元?总计应付款多少元?与一次性付款的差额为多少元?
【例3】购买售价为4万的商品,在三年内按每期付款2.4万元、两次付清总贷款的方式付款,求月利率。
【例4】购买售价均为300![]() 的两条河流A、B汇合于某处后,不断混合,它们的含
的两条河流A、B汇合于某处后,不断混合,它们的含
量分别为2kg/m3和0.2kh/m3,假设从汇合处开始,沿岸设有若干观测点,两股水流经相邻两个观测点的过程中,其混合效果相当于两股水流在单位时间内交换100m3的水量,即从A股流入B股100m3水,经混合后,又从B股流入A股100m3的水并混合,问从第几个观测站开始,两股河水的含沙量之差小于0.01kg/m3(不考虑泥沙沉淀)
【例5】甲、乙两人连续6年对某县农村养鸡业规模进行调查,提供两个不同的信息如下图所示:
甲调查表明∶从第一年每个养鸡场出产1万只鸡上升到第6年平均每个养鸡场出产2万只鸡。
乙调查表明∶由第一年养鸡场个数30个减少到第6年的10个。
请您根据提供的信息说明∶
(1)第2年养鸡场的个数及全县出产鸡的总只数。
(2)到第6年这个县的养鸡业比第一年扩大了还是缩小了?请说明理由。
(3)哪一年的规模最大?请说明理由。
【例6】设![]() 为常数,且
为常数,且![]()
(1)证明:对任意![]() ,
,![]() ;
;
(2)假设对任意![]() ,有
,有![]() ,求
,求![]() 的取值范围。
的取值范围。
双基训练
1、某种细菌在培养过程中,每20分钟分裂一次(一个分裂成2个),经过3小时,这种细菌由一个可繁殖成__________________个
2、一个工厂的产值平均每月增长率为m,则在一年中十二月份产值比一月份增长的百分数是_________________
3、若![]() 是等比数列,
是等比数列,![]() ,
,![]() ,且公比q是整数,则
,且公比q是整数,则![]() ____
____
4、若![]() 表示等差数列
表示等差数列![]() 的前
的前![]() 祥和,已知S9=18,Sn=24,若
祥和,已知S9=18,Sn=24,若![]() ,则
,则![]() =____
=____
5、项数为2m的等比数列,中间两项是方程![]() 的两根,那么这个数列的所有项的和是( )
的两根,那么这个数列的所有项的和是( )
A、![]() B、
B、![]() C、
C、![]() D、不同于以上的答案
D、不同于以上的答案
6、某种产品三次调价,单价由原来的每克512元将到216元,则这种产品平均每次降价的百分率为_______________--
7、1984年年底世界人口达到54.8亿元,若人口的平均增长率为x%,2002年底世界人口数为y 亿,那么y与x的函数关系是_______________
8、有若干台型号相同的联合收割机,收割一片土地上的小麦,若同时投入工作至收割完毕需要24小时;若它们是每隔相同的时间顺序投入工作的,每一台投入工作后都一直工作到小麦收割完毕。如果第一台收割时间是最后一台的5倍,求用这种收割方法收割完这批小麦需要多长时间?
9、已知二次函数![]()
![]()
(1)设函数![]() 的图象的顶点的横坐标构成数列
的图象的顶点的横坐标构成数列![]() ,求证:数列
,求证:数列![]() 是等差数列;
是等差数列;
(2)设函数![]() 的图象的顶点到y轴的距离构成数列
的图象的顶点到y轴的距离构成数列![]() ,求数列
,求数列![]() 的前n项和。
的前n项和。
(3)在(1)的条件下,若数列![]() 满足
满足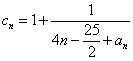
![]() ,求数列
,求数列![]() 中值最大的项和值最小的项。
中值最大的项和值最小的项。
10、已知函数![]()
![]()
(1)求函数![]() 的反函数
的反函数![]() ;
;
(2)对于数列![]() ,设
,设![]() ,
,![]() ,求通项公式
,求通项公式![]() ;
;
(3)设![]() ,
,![]() …+
…+![]() ,求
,求![]()
知识升华
1、等差数列![]() 中,
中,![]() ,它的前11项的平均值是5,若从中抽取1项,余下的平均值是4,则抽取的是( )
,它的前11项的平均值是5,若从中抽取1项,余下的平均值是4,则抽取的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、1990年我国工农业总产值为![]() 千亿元,要实现邓小平同志提出的到2010年工农业总产值翻两番的战略目标,年平均增长率至少应达到____________________
千亿元,要实现邓小平同志提出的到2010年工农业总产值翻两番的战略目标,年平均增长率至少应达到____________________
3、设数列![]() 是首项为50,公差为2的等差数列,
是首项为50,公差为2的等差数列,![]() 是首项为10,公差为4的等差数列,以
是首项为10,公差为4的等差数列,以![]() ,
,![]() 为相邻两边的矩形内最大圆的面积记为
为相邻两边的矩形内最大圆的面积记为![]() ,若
,若![]() ,那么
,那么![]() ____
____
4、从盛满![]() 升纯酒精的容器里到处
升纯酒精的容器里到处![]()
![]() 升,然后用水加满,再倒出
升,然后用水加满,再倒出![]() 升,再用水加满,这样连续倒了
升,再用水加满,这样连续倒了![]() 次后,容器里还有___________________升酒精?
次后,容器里还有___________________升酒精?
5、某人从2001年1月1日起,以后每年1月1日到银行新存入![]() 元(一年定期),若年利率为
元(一年定期),若年利率为![]() 保持不变,且每年到期存款均自动转为新一年定期,到2007年1月1日将所有存款及利息全部收回,他可取回的钱数为________________元
保持不变,且每年到期存款均自动转为新一年定期,到2007年1月1日将所有存款及利息全部收回,他可取回的钱数为________________元
6、一竹梯有11条横档,相邻的档间距离相等,已知最下一档长度为50cm,最上一档长度为40cm,从下到上第7档的应是________cm
7、某县地处水乡,县政府计划从今年起用处理过的生活垃圾填河造地,该县每年以1%的速率减少填河面积,并为保持生态平衡,使填河总面积永远不会超过现有水面的四分之一,则今年所填面积只能占现有面积的百分数为___________-
8、某工厂产量第一年比上一年增加了x%,第二年又增加了m%,为使连续三年的平均增长率为n%,则第三年比第二年应再增加_________________
9、某村镇1992年的人口为1万人,人均住房面积为5m2,若该村镇每年人口的平均增长率为1%,欲使2002年底人均住房面积达10m2,那么每年平均需新建住房________m2
10、电器城有一个体户,一月初向银行贷款10万元作开店资金,每月底获得的利润是该月初投入资金的20%,每月底需交房租和所得税为该月所得金额(含利润)的10%,每月生活费和其它开支3千元,余款作为资金全部投入再营业,如此继续,那么到这一年年底,这位个体户有现款多少元(假设没有赊销)?若银行贷款的年利率为25%,则这位个体户还清银行贷款后,纯收入还有多少?
11、某企业2003年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降,若不进行技术改造,预测从今年起每年比上一年纯利润减少20万元。今年初该企业一次性投入资金600万元进行技术改造,预测在未扣除技术改造资金的情况下,第n年(今年为第一年)的利润为500![]() )万元(n为正整数)
)万元(n为正整数)
(1)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为![]() 万元,进行技术改造后的累计纯利润为
万元,进行技术改造后的累计纯利润为![]() 万元(须扣除技术改造资金),求
万元(须扣除技术改造资金),求![]() ,
,![]() 的表达式。
的表达式。
(2)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
12、对任意函数![]() ,可按右图所示构造一个数列发生器,其工作原理如下:
,可按右图所示构造一个数列发生器,其工作原理如下:
①输入数据![]()
![]() ,经过数列发生器输出
,经过数列发生器输出![]() ;
;
②若![]() ,则数列发生器结束工作;若
,则数列发生器结束工作;若![]() ,则将
,则将![]() 反馈回输入端,再输出
反馈回输入端,再输出![]() ,并依次规律继续下去。现定义
,并依次规律继续下去。现定义![]() 。
。
(1)若输入![]() =
=![]() ,则由数列发生器产生数列
,则由数列发生器产生数列![]() ,请写出数列
,请写出数列![]() 的所有项;
的所有项;
(2)若要数列发生器产生一个无穷的常数列,试求输入的初试数据![]() 的值;
的值;
(3)若输入![]() 时,产生的无穷数列
时,产生的无穷数列![]() 满足:对任意正整数n,均有
满足:对任意正整数n,均有![]() ,求
,求![]() 的取值范围。
的取值范围。
挑战高考
1、如右图所示,在杨辉三角中,斜线AB上方箭头所示的数组成一个锯齿形的数列:1,2,3,3,6,4,10,…,记这个数列的前n项和为![]() 。则
。则![]() =______
=______
2、如图,五角星魅力无穷,一动点由A处按图中数字由小到大的顺序依次运动,当第一次运动结束回到A处时,数字为6,按此规律无限运动,则数字2004应在( )
A、B处 B、C处 C、D处 D、E处
3、某纺织厂的一个车间有n (n>7,![]() 台织布机,编号分别为1,2,3,……,n,该车间有技术工人n 名,编号分别为1,2,3,……,n。定义记号
台织布机,编号分别为1,2,3,……,n,该车间有技术工人n 名,编号分别为1,2,3,……,n。定义记号![]() ,如果第
,如果第![]() 名工人操作了第
名工人操作了第![]() 台织布机,此时规定
台织布机,此时规定![]() =1,否则
=1,否则![]() =0。若第7台织布机有且仅有一人操作,则
=0。若第7台织布机有且仅有一人操作,则![]() ……+
……+![]() =______;若
=______;若![]() +……+
+……+![]() =2说明:_______
=2说明:_______
4、一个热气球在第一分钟时间里上升了25米高度,在以后的每一分钟时间里,它上升的高度都是它在前一分钟里上升高度的80%,这个热气球最多能上升____________米
5、如图:第n个图形是由正![]() 边“扩展”而来,
边“扩展”而来,![]() …)。则第
…)。则第![]() 个图形中共有______________个顶点。
个图形中共有______________个顶点。
6、某种果树至少要培植五年才可以开始采果。有一农户于1991年初利用边角地种植了一批这种果树,1996年开始采果,当年的产量为156千克,1997年至2001年,连续5年每年的产量平均比上一年增加50%还多34千克。从2002年,由于管理等方面的原因导致产量开始下降,且平均每年比上一年减少10%,据估计这种情况还会继续下去。
(1)2001年,该农户采得这种水果多少千克?
(2)如果用![]() 表示该农户从1996年起的
表示该农户从1996年起的![]() 年内采得这种水果的总量,试求出用
年内采得这种水果的总量,试求出用![]() 表示的
表示的![]() 的表达式。并据此计算,到2003年底,该农户共采得这种水果多少千克?(精确到1千克)
的表达式。并据此计算,到2003年底,该农户共采得这种水果多少千克?(精确到1千克)
7、为了保护三峡库区的生态环境,凡是坡度在25°以上的坡荒地都要绿化造林。经初步统计,在三峡库区内坡度大于25°的坡荒地面积约有2640万亩。若从2003年初开始绿化造林,第一年造林120万亩,以后每年比前一年多绿化60万亩。
(1)若所有被绿化造林的坡荒地全部成功,问哪一年底可使库区的坡荒地全部绿化?
(2)若每万亩绿化造林所植树苗的木材量平均为0.1万立方米,每年树木木材量的自然生长率为20%,那么当整个库区25°以上坡荒地全部绿化完的那一年底,一共有木材多少万立方米?(保留一位小数,![]()
![]() )
)