第一节数列的概念
【例1】写出下面数列的一个通项公式，使它的前4项分别是下列各数：
（1）
； （2）
；
（3）
； （4）
【例2】（1）有一数列
，由递推公式
，写出这个数列的前4项，并根据前4项观察规律，写出该数列的一个通项公式。
（2）设数列
中，
，求通项公式。
【例3】数列满足
，求数列的通项公式。
【例4】设是首项为1的正项数列，且
，则它的通项公式
。
【例5】已知数列满足
（1）求
；（2）证明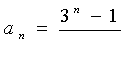
双基训练
1、已知数列
，则其通项可表示为（ ）
A、 B、
C、
D、
2、有下列5个命题：
①数列0，1，0，-1与数列-1，0，1，0是相同的数列；
②数列中不能有相等的项；
③数列2，4，6，8…可表示为
；
④数列1，3，5，2
，…可表示为
；
⑤数列1，2，3…不一定是无穷递增数列。
其中正确命题的个数为（ ）
A、1 B、2 C、3 D、4
3、已知数列中，
，则50是其（ ）
A、第3项 B、第4项
C、第5项 D、不是这个数列的项
4、数列中，
，则此数列的最大项的值是（ ）
A、107 B、108 C、108
D、109
5、数列1，3，6，10，15，…的通项公式
等于（ ）
A、
B、
C、
D、
6、数列
，则它的通项公式是 。
7、已知数列的通项公式为
，则380是这个数列的第 项。
8、若数列由
来确定，求通项公式
9、已知数列中，
，且
，对任意
恒成立，求实数
的取值范围。
10、已知数列的通项
，试问该数列有没有最大项？若有，求出最大项和最大项的项数；若没有，说明理由。
知识升华
1、数列中，
时，
，则（ ）
A、
B、
C、
D、
2、在数列
的每相邻两项中间插入3个数，使它们与原数列构成一个新数列，则新数列的第30项（ ）
A、不是原数列的项 B、是原数列的第7项
C、是原数列的第8项 D、是原数列的第9项
3、已知数列中，
，则
等于（ ）
A、
B、
C、
D、
4、在数列中，
，则该数列中相邻两项乘积是负数的项是（ ）
A、
和
B、和
C、 和
D、和
5、已知数列的前项的和为
，且
，则等于（ ）
A、
B、
C、
D、
6、已知数列的通项公式是
，则数列的最大项是（ ）
A、第12项 B、第12项或第13项
C、第13项 D、不存在
7、已知数列的前项和
，其中
是非零常数，则存在数列
、
使得（ ）
A、
，其中
为等差数列，
为等比数列
B、，其中和都为等差数列
C、
，其中为等差数列，为等比数列
D、，其中和为等比数列
8、数列的前项和
，则
。
9、有穷数列：
，把它的前后顺序改变，即
，则新数列的一个通项公式 。
10、已知数列中，
为的前项和，且
，
求
的值。
11、已知数列满足
求：（1）
的值；
（2）数列的通项公式。
12、设函数
，数列的通项满足
（1）求数列的通项公式；
（2）数列有没有最小的项，若有最小项，试求出此项和相应的项数；若没有最小项，请说明理由。
挑战高考
1、已知数列的通项公式是
，其中均为正常数，那么与
的大小关系是（ ）
A、
B、
C、
D、与的取值相关
2、数列中，
，且
，则
等于（ ）
A、3 B、-3 C、-6 D、6
3、（理）已知数列的通项
，
是数列的前项的各，
即
，当取到最大值时，的值为（ ）
A、9 B、8 C、8或9 D、7或8
（文）已知数列的前项和为
（对于所有
），且
，则的数值是
。
4、设数列的前项和为（对于所有），且，则的数值是
。
5、已知数列中，
为正实数，
（1）若
，求
的取值范围；
（2）求证：不存在，使
对任意恒成立。