第二次调研考试数学参考答案
一、选择题:本大题共10小题,每小题5分,共50分.
1.D 2.A 3.D 4.B 5.C 6.C 7.A 8.A 9.B 10.B
二、填空题:本大题共4小题;每小题4分,共16分.
11.-5 12.![]() 13.(-∞,0]
14.f(x),v(x)
13.(-∞,0]
14.f(x),v(x)
三、解答题:本大题共6小题;共84分.
15.解:(1)若q=1,S3=3 a1,S9=9 a1,S6=6 a1,a1≠0,
则S3+ S6≠2S9,这与S3,S9,S6成等差数列相矛盾. ………………………2分
若q≠1,由S3+ S6=2S9,得![]() . ……………6分
. ……………6分
整理,得 ![]() 。
。
所以 ![]() ,即
,即![]() .
.
由于![]() ,故q=
,故q=![]() . ……………………………………………………8分
. ……………………………………………………8分
(2)由于![]() ,
,
由(1)可知,![]() ,所以
,所以![]() .
.
故a4,a7的等差中项是数列{ an}的第10项.…………………………………14分
16.解:(1)x= a +(t2+1)b=(-2t2-1,t2+3),
y=-k a+![]() b=(-k-
b=(-k-![]() ,-2k+
,-2k+![]() ),………………………………………2分
),………………………………………2分
由x⊥y,得x·y=0,即(-2 t2-1)(-k-![]() ) +(t2+3)
(-2k+
) +(t2+3)
(-2k+![]() )=0.
)=0.
整理,得 ![]() . ……………………………………………………………5分
. ……………………………………………………………5分
∵ t>0,∴![]() ≥2,当且仅当t =1时,k=2.
≥2,当且仅当t =1时,k=2.
所以k的最小值为2 .……………………………………………………………7分
(2)假设存在正实数k,t,使x∥y,则(-2 t2-1)
(-2k+![]() ) =(t2+3)
(-k-
) =(t2+3)
(-k-![]() ).
).
整理,得 t k(t 2+1)+1=0.…………………………………………………………12分
满足上述等式的正实数k、t不存在,所以不存在k、t,使x∥y. ………………14分
17.解法一:(1)由已知AD⊥AB,PD⊥AB,得AB ⊥平面PAD.
点M、N分别是PA、PB的中点,∴ MN∥AB.
∴MN⊥平面PAD,MN⊥PM,MN⊥DM.
∴∠PMD为二面角P—MN—D的平面角.………………………………………4分
Rt△PAD中,由已知∠PAD=60° ,故∠MPD=30°.
∵MD是Rt△PAD斜边PA上的中线,∴MD=MP.
∴△PMD为等腰三角形,∴∠PMD=120° .
故二面角P—MN—D的大小为120° . ……………………………………………8分
(2)① 若∠CDN=90º,则CD⊥平面PDN,而CD⊥平面PAD,故平面PDN与平面PAD重合,与题意不符.……………………………………………………10分
②若∠DCN=90º,由MN∥CD,CD⊥DM,DM⊥MN,得四边形CDMN是矩形,所以 MN=CD,即![]() .………………………………………………………………12分
.………………………………………………………………12分
③ 若∠DNC=90º,连结BD.设AD=a,由已知,得AB=![]() a,从而BD=
a,从而BD=![]() a.
a.
又PD=ADtan60°=![]() a,∴PD=BD.从而DN⊥PB,DN⊥平面PBC.∴DN⊥BC.
a,∴PD=BD.从而DN⊥PB,DN⊥平面PBC.∴DN⊥BC.
又PD⊥BC,∴BC ⊥平面PBD,∴BD⊥BC.
∵CD∥AB,∴∠ABD=∠CDB,∴Rt△ABD∽Rt△CDB.
∴![]() …………………………………15分
…………………………………15分
(2)另解:令![]() 则
则![]()
∵PD⊥平面ABCD,∴Rt△PAD中,可得MD=a.
连结DB,在Rt△PDB中,可得![]()
∵点M、N分别是PA、PB的中点,∴ MN=![]()
在直角梯形MNDC中,
![]() ……10分
……10分
① 若∠CDN=90º,则![]()
∴![]() 这不可能.
这不可能.
②若∠DNC=90º,则![]()
∴![]() 即
即![]() .
.
③ 若∠DCN=90º,则![]()
∴![]() 解得x=0(不合题意,舍去),
解得x=0(不合题意,舍去),![]()
即![]() .………………………………………………………………………15分
.………………………………………………………………………15分
解法二:(1)以D为坐标原点,分别以DA,DC,DP所在直线为x轴,y
轴,z轴建立空间直角坐标系.设AD=a,则AB=![]() a,A(a,0,0),B(a,
a,A(a,0,0),B(a,![]() a,0),C(0,ta,0),P(0,0,
a,0),C(0,ta,0),P(0,0,![]() a),M(
a),M(![]() ,0,
,0,![]() ),N(
),N(![]() ,
,![]() ,
,![]() ),
),
∴![]() =(0,
=(0,![]() ,0)=
,0)=![]() ,所以
,所以![]() ∥
∥![]() .
.
由AB⊥AD,PD⊥AB,AD∩PA=D,得AB⊥平面PAD,
所以∠PMD就是二面角P-MN-D的平面角.
![]() =
=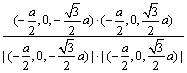 =-
=-![]() ,
,
即二面角P-MN-D的大小为120º. …………………………………………… 8分
(2)① 若∠CDN=90º,则CD⊥平面PDN,而CD⊥平面PAD,故平面PDN与平面PAD重合,与题意不符.…………………………………………………………10分
②若∠DCN=90º,![]() =0,即(0,ta,0)·(
=0,即(0,ta,0)·(![]() ,
,![]() - ta,
- ta,![]() )=0.
)=0.
解得t=![]() ,所以
,所以 ![]() . …………………………………………………12分
. …………………………………………………12分
③ 若∠DNC=90º,则![]() =0,即
=0,即
(![]() ,
,![]() ,
,![]() )·(
)·(![]() ,
,![]() - ta,
- ta,![]() )=0.所以
)=0.所以![]() .
.
解得t=![]() .所以
.所以![]() . ……………………………………………………15分
. ……………………………………………………15分
18.解:方法一 由条件知∠CMB=30 º,∠AMB=45º.
又AB=BC,所以△CBM和△ABM面积相等,
即 ![]() MC·MB·sin30 º=
MC·MB·sin30 º=![]() MA·MB·sin45º .
MA·MB·sin45º .
从而可得MC=![]() .……………………………………………………………5分
.……………………………………………………………5分
在△ACM中,由余弦定理,得 4=MC2+MA2-2MA·MC·cos75°.
所以MA2=![]() .………………………………………………………8分
.………………………………………………………8分
设点M到直线ABC的最小距离为h, h即△ACM的高,由面积关系,得
![]() . ………11分
. ………11分
![]() .
.
答:塔到直路ABC的最短距离为![]() 千米.……………………………13分
千米.……………………………13分
方法二 以点B为坐标原点,BM所在直线为x轴建立直角坐标系,
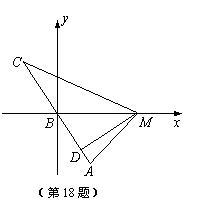 设
设![]() 则
则![]() ……………………………………………2分
……………………………………………2分
可得 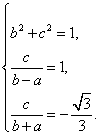
解得![]() .故
.故![]()
直线AB的方程为![]() .……………………………………………8分
.……………………………………………8分
设点M到直线AB的距离为MD,则
![]() 所以
所以![]()
答:塔到直路ABC的最短距离为![]() 千米.………………………………13分
千米.………………………………13分
19.解(1)∵函数![]() 图象向右平移1个单位即得到y=f(x)的图象,并且y=f(x+1)的图象关于点(-1,0)对称,
图象向右平移1个单位即得到y=f(x)的图象,并且y=f(x+1)的图象关于点(-1,0)对称,
∴y=f(x)的图象关于点(0,0)对称,从而对任意实数x,有![]() ,
,
∴![]() =
=![]() ,
,
即![]() 对任意实数x恒成立.
对任意实数x恒成立.
∴![]() ,
,![]()
![]() .
.
![]() 时,
时,![]() 取极大值
取极大值![]() ,
,
∴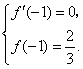 即
即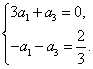 解得
解得![]() .
.
故![]() ………………………………………………………………5分
………………………………………………………………5分
(2)设![]() ,
,![]() 是函数f(x)图象上的两点,则由
是函数f(x)图象上的两点,则由![]() 知两点处的切线斜率分别为
知两点处的切线斜率分别为![]() ,且
,且![]() .
.
∵![]() ,∴
,∴![]()
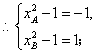 或
或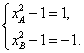
从而可求得两点为(0,0),![]() ,或(0,0),
,或(0,0),![]() . ………10分
. ………10分
(3)证明:∵![]() ( n∈N+) , ∴
( n∈N+) , ∴![]() ,即
,即![]() .
.
又![]() ,∴
,∴![]() , 即
, 即![]() .
.
由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() .
.
∴![]() 在(-1,1)上递减,在(-∞,-1)和(1,+∞)上递增.
在(-1,1)上递减,在(-∞,-1)和(1,+∞)上递增.
又![]() ,
,
![]() ,
,![]() ,
,
而![]() ,
,
∴![]() .……………………………………15分
.……………………………………15分
20.解:设M(x1,y1)为椭圆C上的任意一点(x1y1≠0),N(x2,y2),动点E的坐标为(x,y),
则P (-x1,y1),Q (-x1,-y1),T(x1,-y1).…………………………………1分
所以![]() ,……(1)
,……(1) ![]() . ……(2) …………3分
. ……(2) …………3分
(1)-(2),得![]() .
.
所以![]() ,即
,即![]() . …………………………6分
. …………………………6分
又MN⊥MQ,![]() ,
,![]() ,所以
,所以![]() .
.
直线QN的方程为![]() ,直线PT的方程为
,直线PT的方程为![]() . …10分
. …10分
从而得 ![]() .所以
.所以![]() .
.
由(1),可得![]() ,此即为所求的轨迹方程. ………………13分
,此即为所求的轨迹方程. ………………13分