第二节函数的单调性和奇偶性
【例1】利用函数单调性定义证明函数![]() 在
在![]() 上是减函数。
上是减函数。
【例2】定义在R上的函数![]() ,当
,当![]() 时,
时,![]() ,且对任意的
,且对任意的![]() ,有
,有![]()
(1)证明:![]() ;(2)证明:对任意的
;(2)证明:对任意的![]() ,恒有
,恒有![]() ;
;
(3)证明:![]() 是R上的增函数;(4)若
是R上的增函数;(4)若![]() ,求
,求![]() 的取值范围。
的取值范围。
【例3】讨论下列函数的单调性
(1)![]() (2)
(2)![]() (3)
(3)![]()
【例4】讨论函数![]() 在
在![]() 上的单调性。
上的单调性。
【例5】求函数![]() 的单调增区间。
的单调增区间。
【例6】求函数![]() 的单调区间。
的单调区间。
【例7】设二次函数![]()
(1)若![]() 的单调递增区间是
的单调递增区间是![]() ,求实数
,求实数![]() 的值;
的值;
(2)若![]() 在区间
在区间![]() 内是增函数,求实数
内是增函数,求实数![]() 的取值范围。
的取值范围。
【例8】讨论下述函数的奇偶性:
(1)![]() ;(2)
;(2)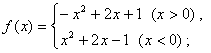
(3)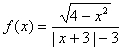 ;(4)
;(4)![]() (常数
(常数![]() )
)
【例9】设定义在![]() 上的偶函数
上的偶函数![]() 在区间
在区间![]() 上单调递减,若
上单调递减,若
![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
【例10】已知![]() 是奇函数,它在
是奇函数,它在![]() 上是增函数,且
上是增函数,且![]() ,试问
,试问![]() 在
在![]() 上是增函数还是减函数?证明你的结论。
上是增函数还是减函数?证明你的结论。
【例11】设![]() 的定义域为
的定义域为![]() ,且在
,且在![]() 上为增函数,
上为增函数,![]()
(1)求证![]() ;
;
(2)设![]() ,解不等式
,解不等式![]()
双基训练
1、下述函数中,在![]() 内为增函数的是( )
内为增函数的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、下述函数中,单调递增区间是![]() 的是( )
的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、若函数![]() 在
在![]() 内为减函数,则实数
内为减函数,则实数![]() 的取值是( )
的取值是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、若函数![]() 在
在![]() 内单调递减,而在
内单调递减,而在![]() 内为增函数,则
内为增函数,则![]() 的值为( )
的值为( )
A、1 B、
5、已知![]() 是奇函数,那么实数
是奇函数,那么实数![]() 的值等于( )
的值等于( )
A、1 B、-1 C、0 D、![]()
6、对于任意定义在R上的函数![]() ,若实数
,若实数![]() 满足
满足![]() ,则称
,则称![]() 是函数
是函数![]() 的一个不动点,若函数
的一个不动点,若函数![]() 没有不动点,则实数
没有不动点,则实数![]() 的取值范围是 。
的取值范围是 。
7、要使函数![]() 在
在![]() 上存在反函数,则
上存在反函数,则![]() 的取值范围是 。
的取值范围是 。
8、解答下列问题:
(1)定义在![]() 上的奇函数
上的奇函数![]() 在定义上是减函数,且
在定义上是减函数,且![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
(2)设函数![]() 是奇函数,在
是奇函数,在![]() 是一个恒小于零的减函数,试问
是一个恒小于零的减函数,试问![]() 在
在![]() 上是增函数还是减函数?证明你的结论。
上是增函数还是减函数?证明你的结论。
9、已知定义域为![]() 的函数
的函数![]() 满足:
满足:
①![]() 时,
时,![]() ;②
;②![]() ;③对任意的正实数
;③对任意的正实数![]() ,都有
,都有![]()
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 在定义域内为减函数;
在定义域内为减函数;
(Ⅲ)求不等式![]() 的解集。
的解集。
10、已知函数![]() 为奇函数,
为奇函数,![]() ,若
,若![]() 在
在![]() 内为增函数,而在
内为增函数,而在![]() 内为减函数,求
内为减函数,求![]() 的解析式。
的解析式。
知识升华
1、如果奇函数![]() 在区间
在区间![]() 上是增函数,且最小值为
上是增函数,且最小值为![]() ,那么
,那么![]() 在区间
在区间![]() 上是( )
上是( )
A、增函数且最小值为![]() B、增函数且最大值为
B、增函数且最大值为![]()
C、减函数且最小值为![]() D、减函数且最大值为
D、减函数且最大值为![]()
2、已知![]() 为偶函数,在
为偶函数,在![]() 上为减函数,若
上为减函数,若![]() ,则方程
,则方程
![]() 的根的个数是( )
的根的个数是( )
A、2 B、2或1 C、3 D、2或3
3、已知![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() ,那么
,那么![]() 的值是( )
的值是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、定义在R上的函数![]() 满足
满足![]() ,当
,当![]() 时,
时,![]() ,
,
则不等式![]() 的解集是( )
的解集是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
5、设![]() 是R上的减函数,则下列关系成立的是( )
是R上的减函数,则下列关系成立的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
6、已知偶函数![]() 在
在![]() 上单调递增,那么下列关系成立的是( )
上单调递增,那么下列关系成立的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
7、设函数![]() 为奇函数,
为奇函数,![]() ,则
,则![]() ( )
( )
A、0 B、1 C、![]() D、5
D、5
8、对于函数![]() ,下列性质正确的是有
,下列性质正确的是有
①对于![]() ,都有
,都有![]() ②在
②在![]() 上函数
上函数![]() 单调递减
单调递减
③在![]() 上函数
上函数![]() 单调递增 ④
单调递增 ④![]() 不是函数
不是函数![]() 的最小值
的最小值
(请把正确的序号都填上,不能多填也不能少填)
9、![]() 是定义在R上的偶函数,其图象关于
是定义在R上的偶函数,其图象关于![]() 对称,且当
对称,且当![]() 时,
时,
![]() ,则当
,则当![]() 时,
时,![]() 。
。
10、已知函数![]() 的图象与函数
的图象与函数![]() 的图象关于点
的图象关于点![]() 对称。
对称。
(1)求![]() 的值;
的值;
(2)若![]() 在区间
在区间![]() 上为减函数,求实数
上为减函数,求实数![]() 的取值范围。
的取值范围。
11、函数![]() 的定义域是R,对任意
的定义域是R,对任意![]() 都有
都有![]() ;且
;且![]() 时,
时,![]() ,求
,求![]() 在
在![]() 上的最大值和最小值。
上的最大值和最小值。
12、设函数![]() 是奇函数
是奇函数![]() ,且
,且![]()
(1)求![]() 的值;
的值;
(2)判断并证明![]() 在
在![]() 上的单调性。
上的单调性。
挑战高考
1、函数![]() 的反函数为( )
的反函数为( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
2、已知对任意![]() 都有
都有![]() ,且当
,且当![]() 时,
时,![]() ,
,
则![]() ( )
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、(理)设奇函数![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,若函数
,若函数![]() 对所有的
对所有的![]() 都成立,当
都成立,当![]() 时,则
时,则![]() 的取值范围是( )
的取值范围是( )
A、![]() B、
B、![]()
C、![]() 或
或![]() 或
或![]() D、
D、![]() 或
或![]() 或
或![]()
(文)已知函数![]() 在定义域
在定义域![]() 内存在反函数,且
内存在反函数,且![]() ,则
,则![]() ( )
( )
A、-4 B、-3 C、-2 D、-1
4、函数![]() 在区间
在区间![]() 上存在反函数的充分必要条件是( )
上存在反函数的充分必要条件是( )
A、![]() B、
B、![]()
C、![]()
![]() D、
D、![]()
5、设函数![]() 是定义在R上的奇函数,若
是定义在R上的奇函数,若![]() 的最小正周期为3,且
的最小正周期为3,且![]() ,
,
![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A、![]() B、
B、![]() 且
且![]()
C、![]() D、
D、![]() 或
或![]()
 6、已知函数
6、已知函数![]() 是R上的减函数,
是R上的减函数,![]() 是其图象上的两点,那么不等式
是其图象上的两点,那么不等式![]() 的解集是( )
的解集是( )
A、![]()
B、![]()
C、![]()
D、![]()
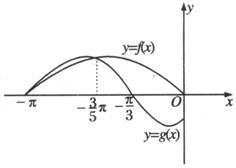
7、已知函数![]() 是奇函数,
是奇函数,![]() 是偶函数,它们的定义域为
是偶函数,它们的定义域为![]() ,且它们在
,且它们在![]() 上的图像如上图所示,则不等式
上的图像如上图所示,则不等式![]() 的解集为 。
的解集为 。
8、已知函数![]() 满足:
满足:![]() ,则
,则![]()
![]()
![]() 。
。
9、函数![]() 在
在![]() 上是减函数,函数
上是减函数,函数![]() 是偶函数,则有( )
是偶函数,则有( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
10、设函数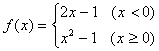 ,则
,则![]() 的值是( )
的值是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11、定义在R上的函数![]() 满足
满足![]() ,且函数
,且函数![]() 为奇函数,
为奇函数,
给出下列命题:①函数![]() 的最小正周期为
的最小正周期为![]() ;②函数
;②函数![]() 的图象关于点
的图象关于点
![]() 对称;③函数
对称;③函数![]() 的图象关于
的图象关于![]() 轴对称。其中真命题的个数是( )
轴对称。其中真命题的个数是( )
A、3 B、2 C、1 D、0
12、定义在R上的偶函数![]() 在
在![]() 上递减,且
上递减,且![]() ,则满足
,则满足
![]() 的
的![]() 的集合为( )
的集合为( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
13、若函数![]() 是奇函数,且方程
是奇函数,且方程![]() 有三个根
有三个根![]() 、
、![]() 、
、![]() ,则
,则![]() +
+![]() +
+![]() 的值
的值
( )
A、是-1 B、是3 C、是0 D、不确定