文理科续篇部分内容练习题——极坐标
一、极坐标系:
1、将下列直角坐标系的点的坐标化为极坐标(要求![]() ):
):
A![]() :_____;B
:_____;B![]() :____;C(2,-1):______;D(-2,-2):_____
:____;C(2,-1):______;D(-2,-2):_____
注意:1、![]() 时,点A的位置没有变化,只是
时,点A的位置没有变化,只是![]() 表示点A到原点的距离,
表示点A到原点的距离,![]() 表示ox轴绕着原点旋转到与OA重合的角的大小。
表示ox轴绕着原点旋转到与OA重合的角的大小。
2、![]() 时,
时,![]() 表示点A到原点的距离的相反数,
表示点A到原点的距离的相反数,![]() 表示ox轴绕着原点旋转到与OA的反向延长线重合的角的大小。
表示ox轴绕着原点旋转到与OA的反向延长线重合的角的大小。
练习:将上述四点化为极坐标(要求![]() ):
):
A![]() :_____;B
:_____;B![]() :____;C(2,-1):______;D(-2,-2):_____
:____;C(2,-1):______;D(-2,-2):_____
二、极坐标与直角坐标的互化:![]()
练习:将下列极坐标系的点的坐标化为直角坐标:
A![]() :_____;B
:_____;B![]() :______;C:
:______;C:![]() _____;D
_____;D![]() :______
:______
三、直线的极坐标方程:
(一)将下列直线的极坐标方程化为直角坐标方程:
1、![]() 2、
2、![]()
3、![]() 4、
4、![]()
5、![]()
(二)求符合下列条件的直线的极坐标方程:
1、经过极点,倾斜角为![]() ; 2、经过点A(5,0),和极轴垂直;
; 2、经过点A(5,0),和极轴垂直;
3、经过点B(3,![]() )且和极轴垂直;
)且和极轴垂直;
4、经过点B(3,![]() )且和极轴平行。
)且和极轴平行。
四、圆的极坐标方程:
(一)将下列圆的极坐标方程化为直角坐标方程:
1、![]() ; 2、
; 2、![]() ; 3、
; 3、![]()
(二)求符合下列条件的圆的极坐标方程:
1、圆心为A![]() ,半径为a; 2、圆心为A
,半径为a; 2、圆心为A![]() ,半径为a;
,半径为a;
(三)求下列圆的圆心和半径的极坐标:
1、![]() ; 2、
; 2、![]()
直线的参数方程的几何意义
一、直线的参数方程的形式: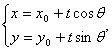 (t为参数)
(t为参数)
二、直线的参数方程的特点:
(1)点![]() 是直线上的一个已知点;
是直线上的一个已知点;
(2)点![]() 是直线上的动点;
是直线上的动点;
(3)![]() 是直线的倾斜角,且作为t的系数的
是直线的倾斜角,且作为t的系数的![]() 的平方和为1。
的平方和为1。
若直线方程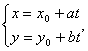 (t为参数)中的系数a,b的平方和不为1,则提取
(t为参数)中的系数a,b的平方和不为1,则提取![]() 后将方程化为
后将方程化为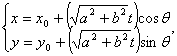
其中![]()
(4)参数t的几何意义是:动点P到定点![]() 的有向线段的长度。
的有向线段的长度。
(5)若直线与某一直线相交,在只需将直线的参数方程代入直线方程后,得到关于t的方程。求出t,在t的绝对值就是焦点到定点![]() 的距离;若直线与某一圆锥曲线相交于两点,在只需将直线的参数方程代入圆锥曲线方程后,得到关于t的一元二次方程,则
的距离;若直线与某一圆锥曲线相交于两点,在只需将直线的参数方程代入圆锥曲线方程后,得到关于t的一元二次方程,则![]() 就是两个交点间的距离。
就是两个交点间的距离。
三、直线的参数方程的应用:
1、过![]() 的直线l:
的直线l: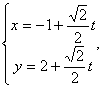 (t为参数)
(t为参数)
(1)与直线l1:![]() 交于点Q,求|PQ;
交于点Q,求|PQ;
(2)与⊙O:![]() 交于M、N两点,求
交于M、N两点,求![]() 的值及线段MN的长。
的值及线段MN的长。
2、直线l: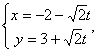 (t为参数)上到点A(-2,3)的距离等于
(t为参数)上到点A(-2,3)的距离等于![]() 的点的坐标为_________________________________。
的点的坐标为_________________________________。
3、直线l1:过点P(0,-2),且倾斜角为![]() ,直线l2:
,直线l2:![]() ,直线l1、 l2交于点Q,求|PQ。
,直线l1、 l2交于点Q,求|PQ。
4、过点A(1,3)的直线l与x,y轴分别交于P、Q两点。求使![]() 最小时直线l的方程。
最小时直线l的方程。
工序流程图练习
班级________姓名___________
1、某工程的工序流程图如下:(工时数单位:天),求出工程总时数。
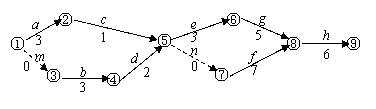 |
2、某工程由下列工序组成:
| 工序 | a | b | c | d | e | f | g | h | i |
| 紧前工序 | - | - | - | a | b,c,d | b,c,d | f | g | e,h |
| 工时数(天) | 2 | 7 | 15 | 8 | 12 | 6 | 4 | 5 | 10 |
试画出工序流程图,并求出关键路线与工程总时数。
3、某个任务包含9道工序:a,b,c,d,e,f,g,h,i,各道工序所需的时间依次是:5,6,8,9,4,7,4,5,6(天),它们之间的先后顺序及相互关系是:a完成后,b可以开工;b完成后,c,d可以同时开工;c完成后,e可以开工;d完成后,g可以开工;d,e完成后,f可以开工;g完成后,h可以开工;f,h完成后,i可以开工。画出这个任务的工序流程图,并求出关键路线和工程总时数。
4、某个任务包含8道工序:a,b,c,d,e,f,g,h ,各道工序所需的时间依次是:5,5,3,4,5,9,7,8(天),它们之间的先后顺序及相互关系是:a,b可以同时开工;a完成后,c可以开工;b完成后,d可以开工;c,d完成后,e,f可以同时开工;e完成后,g可以开工;f,g完成后,h可以开工。画出这个任务的工序流程图,并求出关键路线和工程总时数。
5、某工程由下列工序组成,试画出这个任务的工序流程图,并求出关键路线和工程总时数。
| 工序 | a | b | c | d | e | f | g | h |
| 紧前工序 | - | - | a | b | a,d | c,e | c | f,g |
| 工时数(天) | 3 | 6 | 9 | 7 | 5 | 4 | 2 | 1 |
《简单的线性规划》练习
班级________姓名___________
1、当x、y满足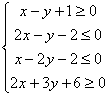 时,求目标函数k=2x-3y的最大值与最小值。
时,求目标函数k=2x-3y的最大值与最小值。
2、某造纸厂用废纸与木浆为原料,生产甲、乙两种纸。生产每种纸一吨所需原料、纯利润与每日原料限额如下表:
| 生产每吨纸 | 需废纸(吨) | 需木浆纸(吨) | 纯利润(元) |
| 甲种 | 0 | 20 | 100 |
| 乙种 | 2 | 5 | 70 |
| 每日原料限额 | 10 | 45 |
该如何安排两种纸的日产量,使每日获得的利润最高?
3、已知x,y满足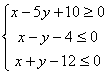 ,求目标函数
,求目标函数![]() 的最值。
的最值。
5、已知x,y满足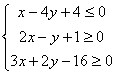 ,求目标函数
,求目标函数![]() 的最大值。
的最大值。
6、已知x,y满足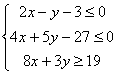 ,求目标函数
,求目标函数![]() 的最大值和最小值及此时x、y的值。
的最大值和最小值及此时x、y的值。
7、已知![]() 满足
满足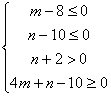 ,求目标函数
,求目标函数![]() 的最值。
的最值。
8、今有56cm的钢材余料,要截取长度为8cm和13cm两种规格的钢材,怎样截取,才能使这根钢材余料得到充分利用?
9、今有236cm的木料,要截取长度为30cm和50cm两种规格的小木料,怎样截取,才能使这根木材得到充分利用,使剩料最少?
10、某建筑工程队需要招聘技术工人和熟练工30人到60人,其中技术工人不少于熟练工人的![]() ,且技术工人的月工资为400元,熟练工的月工资为300元。在这样的条件下,应怎样招聘才能使工程队支出的月工资总数最少?
,且技术工人的月工资为400元,熟练工的月工资为300元。在这样的条件下,应怎样招聘才能使工程队支出的月工资总数最少?