1、(案中)已知平面上一点C(—1,0)和一条直线![]() =
=![]() ,P为该平面上一动点,作PQ⊥
,P为该平面上一动点,作PQ⊥![]() ,垂足为Q,(
,垂足为Q,(![]() )(
)(![]() )=0
)=0
(1) 问点P在什么曲线上,求出该曲线的方程。
(2)
点O在坐标原点,A,B两点在点P的轨迹上,若![]() (
(![]() )
)![]() ,求λ的取值范围。
,求λ的取值范围。
解(1):设P(x,y)∵(![]() )(
)(![]() )=0
)=0
∴![]() =0,代入得(x+4)2=4((x+1)2+y2)
=0,代入得(x+4)2=4((x+1)2+y2)
化简得:![]() ,所以点P在椭圆
,所以点P在椭圆![]() 上。
上。
(2)∵![]() ∴移项得
∴移项得![]() ,即
,即![]() 和
和![]() 共线
共线
∴A,B,C三点共线 ∵在椭圆方程中a2=4,b2=3
∴c2=1,c=1,C(-1,0)恰好为椭圆的左焦点,由图形可知当A,B两点分别为椭圆长轴的两个顶点时,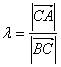 取最值,∵a+c=3, a-c=1∴λmax=
取最值,∵a+c=3, a-c=1∴λmax=![]()
∴λ∈[![]() ]
]
2、(案中)A有一只放有x个红球,y个白球,z个黄球的箱子(x、y、z≥0,![]() ),B有一只放有3个红球,2个白球,1个黄球的箱子,两人各自从自己的箱子中任取一球比颜色,规定同色时为A胜,异色时为B胜.
),B有一只放有3个红球,2个白球,1个黄球的箱子,两人各自从自己的箱子中任取一球比颜色,规定同色时为A胜,异色时为B胜.
(1)用x、y、z表示B胜的概率;
(2)当A如何调整箱子中球时,才能使自己获胜的概率最大?
解:(1)显然A胜与B胜为对立事件,A胜分为三个基本事件:
①A1:“A、B均取红球”;②A2:“A、B均取白球”;③A3:“A、B均取黄球”.
![]()
![]()
![]()
(2)由(1)知![]() ,
,![]()
于是![]() ,即A在箱中只放6个红球时,获胜概率最大,其值为
,即A在箱中只放6个红球时,获胜概率最大,其值为![]()
3、(案中)对于函数![]() (
(![]() ,
,![]() 为函数的定义域),若同时满足下列条件:①
为函数的定义域),若同时满足下列条件:①![]() 在定义域内单调递增或单调递减;②存在区间
在定义域内单调递增或单调递减;②存在区间![]() ,使
,使![]() 在
在![]() 上的值域是
上的值域是![]() .那么把
.那么把![]()
![]() 称为闭函数.
称为闭函数.
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)判断函数![]()
![]() 是否为闭函数?并说明理由.
是否为闭函数?并说明理由.
(3)若![]() 是闭函数,求实数
是闭函数,求实数![]() 的取值范围.
的取值范围.
解:(1)由![]() 在
在![]() 上为减函数,得
上为减函数,得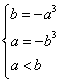 ,可得
,可得![]() ,
,![]() ,
,![]() 所求区间是
所求区间是![]() .
.
(2)∵f'(x)=![]() =
=![]() ,∴当
,∴当![]() ,f'(x)≤0,f(x)为减函数,当
,f'(x)≤0,f(x)为减函数,当![]() ,f'(x)≥0,f(x)为增函数,∴f(x)在(0,+∞)上不是单调函数。所以
,f'(x)≥0,f(x)为增函数,∴f(x)在(0,+∞)上不是单调函数。所以![]() 不是闭函数。
不是闭函数。
(3)设函数符合条件②的区间为![]() ,则
,则
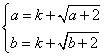 ,故
,故![]() ,
,![]() 是方程
是方程![]() 的两个实根,
的两个实根,
命题等价于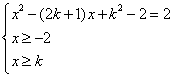 有两个不等实根.
有两个不等实根.
当![]() 时,
时,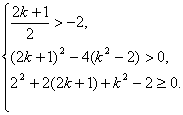 解得
解得![]() ,
,
![]()
![]() ;当
;当![]() 时,
时,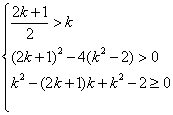 这时,
这时,![]() 无解.
无解.
所以![]() 的取值范围是
的取值范围是![]() .
.
4、(案中)由原点O向三次曲线 ![]() 引切线,切点为P1
引切线,切点为P1![]() (O,P1两点不重合),再由P1引此曲线的切线,切于点P2
(O,P1两点不重合),再由P1引此曲线的切线,切于点P2![]() (P1,P2不重合),如此继续下去,得到点列:
(P1,P2不重合),如此继续下去,得到点列:![]() .
.
(1)求![]() ;
;
(2)求![]() 与
与![]() 满足的关系式;
满足的关系式;
(3)
若![]() ,试判断
,试判断![]() 与
与![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
解:(1)由![]() 得
得![]() 过曲线上的点P1
过曲线上的点P1![]() 的切线L1的方程为
的切线L1的方程为![]() 又∵切线L1过原点O,有
又∵切线L1过原点O,有![]() 化得
化得![]() .
.
(2)过曲线上的点![]() 处的切线
处的切线![]() 方程为
方程为
![]()
![]() 过点
过点![]() 得
得![]()
由于![]() ,分解因式并约简,得
,分解因式并约简,得![]()
∴![]()
![]()
∴![]() .
.
(3)由(2)得:![]() ,∴
,∴![]()
故有数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
∴![]() ,∴
,∴![]()
∵![]() ,∴当
,∴当![]() 为偶数时,
为偶数时,![]() ;当
;当![]() 为奇数时
为奇数时![]() .
.