一、选择题
1. 设集合
，若
，则实数m的取值范围是
（A）m≥-1 （B）m>-1 （C）m≤-1 （D）m<-1
2. 命题
≤
是命题
≥
或
≤
(A)充分非必要条件 (B)必要非充分条件 (C)充分必要 (D)既非充分又非必要条件
3. 从分别写有A、B、C、D、E的5张卡片中，任取2张，这2张卡片上的字母恰好按字母顺序相邻的概率是(A)
(B)
(C)
(D)
4. 设P（x,y）是曲线
（
为参数，
）上任意一点，则
的取值范围是
（A）
（B）
（C）
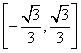（D）
5. 若
是偶函数，且在
内是增函数，又
，则
的解集是（ ）
(A)
(B)
(C)
(D)
6. 方程 x (x2 + y2－3) = 0与x2 + (x2 + y2－3)2 = 0所表示的曲线是
(A)都表示一条直线和一个圆 (B)都表示两个点
(C)前者是两个点，后者是一条直线和一个圆(D)前者是一条直线和一个圆，后者是两个点
7. 已知凸函数的性质定理：“若函数f(x)在区间D上是凸函数，则对于区间D内的任意
有：
”若函数y=sinx在区间（0，π）上是凸函数，则在△ABC中，
的最大值是（ ）（A） （B） (C）
（D）
8. 已知双曲线的中心在原点，两个焦点为F1 (－
，0)和F2 (，0)，P在双曲线上，满足
＝0且△F1PF2的面积为1，则此双曲线的方程是
A．
B．
C．
D．
9. 已知定义在
上的偶函数在
上是增函数，且
，则
的的取值范围 (A) (B)
(C)
(D)
10. 设平面
A、B∈平面
,点C∈平面
,且A、B、C均不在直线l上.给出四个命题：
①
②
③
④
其中正确的命题是（ ）
A．①与② B．②与③ C．①与③ D．②与④
11. 已知直线
与曲线
切于点（1，3），则b的值为 （ ）
A．3 B．－3 C．5 D．－5
12. 设奇函数
上是增函数，且
若函数
对所有
的
都成立，当
时，则t的取值范围是 （ ）
A．
B．
C．
D．
二、填空题
13. 若
的展形式中各项系数的和为128，则展开式中
项的系数为____________.
14. 
是正实数，如果函数
在
上是增函数，那么的取值范围是 .
15. 在数列
中,
是它的前n项和，且
则它的通项公式是
=______________________。
16. 在等差数列｛｝中，当
时，｛｝必定是常数数列。然而在等比数列｛｝中，对某些正整数
、
，当时，非常数数列｛｝的一个例子是____________.
三、解答题
17. 用分期付款的方式购买一批总价为2300万元的住房，购买当天首付300万元，以后每月的这一天都交100万元，并加付此前欠款的利息，设月利率为1%，若首付300万元之后的第一个月开始算分期付款的第一个月，问分期付款的第10个月应付多少万元？全部贷款付清后，买这批房实际支付多少万元？
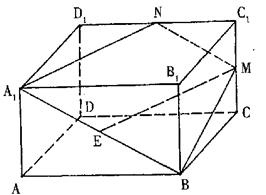
18. 如图，在正四棱柱ABCD—A1B1C1D1中，
，点E，M分别为A1B，C1C的中点，过点A1，B，M三点的平面A1BMN交C1D1于点N.(Ⅰ)求证:EM//平面A1B1C1D1;(Ⅱ)求二面角B—A1N—B1的正切值.
|
参考答案
一选择题1.D 2.A 3.B 4.C 5.C 6. D 7.C 8.C 9.B 10.D 11.A 12.C
二填空题13.-189 14.0<ω≤ 15.2n-1 16.a,-a,a,-a,…
三解答题
17. 解：购买时付款300万元，则欠款2000万元，依题意分20次付清，则每次交付欠款的数额顺次构成数列{an},（2分）
故a1=100+2000×0.01=120(万元)
a2=100+(2000-100)×0.01=119(万元)
a3=100+(2000-100×2)×0.01=118(万元)
a4=100+(2000-100×3)×0.01=117(万元)（4分）
… … …
故a10=121-10=111（万元） （8分）
a20=121-20=101（万元）
20次分期付款的总和为
实际要付出300+2210=2510（万元） （12分） 答：略
18. （Ⅰ）证明：设A1B1的中点为F，连接EF，FC1
∵E为A1B的中点 ∴EF∥
B1B
又C1M∥B1B ∴EF∥MC1
∴四边形EMC1F为平行四边形
∴EM∥FC1…………2分 ∵EM
平面A1B1C1D1，FC1
平面A1B1C1D1
∴EM∥平面A1B1C1D1………………4分
（Ⅱ）解：作B1H⊥A1N于H，连接BH
∵BB1⊥平面A1B1C1D1，∴BH⊥A1N ∴∠BHB1为二面角B—A1N—B1的平面角…………7分
∵EM∥平面A1B1C1D1，EM平面A1BMN 平面A1BMN∩平面A1B1C1D1=A1N，∴EM∥A1N
又∵EM∥FC1， ∴A1N∥FC1 又∵A1F∥NC1，∴四边形A1FC1N是平行四边形
∴NC1=A1F……10分 设AA1=α，则A1B1=2α，D1N=α
在Rt△A1D1N中，A1N=
在Rt△A1B1H中，
在Rt△BB1H中，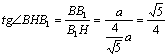
……12分