三角函数精品专题：三角函数中的三角变换
一、首变变角，即在解决三角变换的题目时，首先看看已知角与所求角有没有关系。
一般是：寻找已知角与所求角相加、相减、倍半关系及与特殊角的关系。
1、函数y=
的周期为 （ C
）
A.
B.
C.π
D.2π
2、已知sinα＝
，α∈(，π)，tan(π－β)＝
，求tan(α－2β)的值
答案： tan(α－2β)=
3、在
（ A）
A 
B 
C或 D 
4、函数
的最大值是
7
。
5、已知
，若α在第二象限内，则
值等于（ A ）
A．
B．
C．
D．以上答案都不对
6、设
为第四象限的角，若
，则
7、已知
， （1）求sin2x的值；
（2）又若
，求
的值。
答案：(1) 
(2)
二、次变变名，即在解决三角变换的题目时，要从整体上看看名称之间的联系。
一般是：切化弦（通分）、异名化同名、诱导公式、
1、已知
，则
。
2、
= 
。
3、要得到函数y＝cos(2x－
)的图象，只需将函数y＝sin2x的图象
（ A ）
A.向左平移
个单位
B.向右平移个单位
C.向左平移个单位
D.向右平移个单位
三、主变变式，即在解决三角变换的题目时，主要考查的是式子的变化。
一般是：诱导公式、巧用“1”、升幂降幂公式、黄金组合、
1、
的值为
（
B ）
A.
B.
C.
D.
2、(1+tan21°)(1+tan22°)(1+tan23°)(1+tan24°)的值是 （ C ）
A.16 B.8 C.4 D.2
3、已知tan(＋θ)＝3，则sin2θ－2cos2θ的值为 
4、已知
为第二象限角，且
，那么
的取值范围是（ D
）
A．
B．
C．
D．
5、函数
的最小值是 （ B ）
A.
B.
C.
D.
6、已知
，则
的取值范围是 
7、已知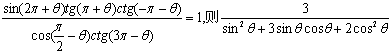
的值是（ A
）
A.1 B.2 C.3 D.6
7、设函数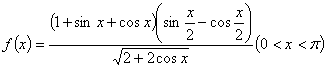
（1）化函数为最简形式 
答案：
四、三大变换的综合运用：
1、已知
，求
的值。
答案：
2、已知
，且
，求
答案：
3、在三角形ABC中，
，
，求
答案：
4、已知
，求
的值。
答案：