三角函数练习

三角函数练习

　　　　　　　　　　　　　　　　　　　　　　　　

一、选择题

1、是第二象限角，则必须有　　　　　　　　　　　　　　　　　　　　　  （　　　）

　A　　B　 C　 D　

2．设分别是的三个内角所对的边，则是的（）（A）充分条件 （B）充分而不必要条件 （C）必要而充分条件 （D）既不充分又不必要条件

3、设，若关于的不等式在区间上恒成立，则 （　　 ）

A　　　B　[-1，0]　  C　 　　D　　[0，1]

4．已知函数（、为常数，，）在处取得最小值，则函数是　　　　　　　　　　　　　　　　　  （　　 ）

A．偶函数且它的图象关于点对称 　B．偶函数且它的图象关于点对称

C．奇函数且它的图象关于点对称 D．奇函数且它的图象关于点对称

5．函数在上的最小值是，则的最小值等于（　　）

　　（A）　　　　（B）　　　　（C）2　　　　（D）3

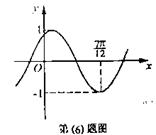6．将函数的图象按向量平移，平移后的图象如图所示，则平移后的图象所对应函数的解析式是（　 ）　　　 A．　B．

C．　D．

7、函数的图像如图，则函数在上的图像大致为（　　　）

8．如果的三个内角的余弦值分别等于的三个内角的正弦值，则（　 ）

A．和都是锐角三角形　　　B．和都是钝角三角形

C．是钝角三角形，是锐角三角形

D．是锐角三角形，是钝角三角形

9、若圆至少能盖住函数的一个最大值和一个最小值点，则的取值范围是　　　　　　　　　　　　　　　　　　　　　　 （　 ）

A　　B　 　C　 　 D　以上都不对

10、已知，是方程的两个根，则的值为　　　　　　　　　　　　　　　　　　　　　　 （　 ）

A　 　B　 　 C　 　　D　　

二、填空题

11、函数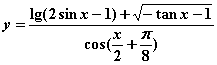的定义域为　　　　　　　　　　　　　

12、已知函数，则=　　　　　　　  ，

=　　　　　　　　　　　　 

13、已知函数，则　　　　　　　 

14、函数的反函数为，则的解是　　　　　　　　　　 

15、函数的图像与直线有且仅有两个不同的交点，则的取值范围是　　　　　　　　　　　　

16、函数，给出以下四个结论：

（1）周期为　　（2）图像关于直线　 （3）图像关于点对称

（4）在区间（）上是增函数

以其中两个论断为条件，令两个论断为结论写出一个你认为正确的一个命题：　　　　　　　 

三、解答题

17、设函数f(x)=+sincos+a(其中＞0,aR),且f(x)的图象在y轴右侧的第一个高点的横坐标为.

（Ⅰ）求ω的值；　　 （Ⅱ）如果f(x)在区间上的最小值为，求a的值.

18、已知函数

（1）求它的定义域和值域　　　 （2）判断它的奇偶性

（3）判断它的单调区间及每一区间上的单调性

（4）判断它的周期性，如果是周期函数，求出它的最小正周期

19、偶函数在有定义，且在上是减函数，设，求时的取值范围。

20、已知函数的图像与轴在原点右侧的第一个交点为N（6，0），又

（1）求这个函数的解析式　

（2）设关于的方程在[0，8]内有两个不同的根，求的值及的取值范围。