上学期高三月考试卷数学试题(三)
数学试题(理)
时间:120分钟 满分:150分
一、选择题:本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合![]() ,集
,集![]() ,则集合
,则集合![]() 为( )
为( )
A.![]() B.
B.![]() C
C![]() D.
D.![]()
2.已知直线l的方程是![]() ,与直线l垂直的一条直线的方程是( )
,与直线l垂直的一条直线的方程是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
3.已知f(x)在![]() 上是减函数,且f(1-m)<f(m-3),则m的取值范围是 ( )A.m<2
B.0<m<1 C.0<m<2
D.1<m<2
上是减函数,且f(1-m)<f(m-3),则m的取值范围是 ( )A.m<2
B.0<m<1 C.0<m<2
D.1<m<2
4.![]() 是等差数列,S10>0,S11<0,则使
是等差数列,S10>0,S11<0,则使![]() <0的最小的n值是
(
)A.5 B.6
C.7 D.8
<0的最小的n值是
(
)A.5 B.6
C.7 D.8
5.已知函数![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6..已知a>3,![]() ,则p,q的大小关系为
( )A.p<q
B.p>q C.p≤q
D.p≥q
,则p,q的大小关系为
( )A.p<q
B.p>q C.p≤q
D.p≥q
7.设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则
,则![]() 等于( )
等于( )
A.18 B.36 C.45 D.60
8.已知两点A(3,2)和B(-1,4)到直线![]() 距离相等,则m为( )
距离相等,则m为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.要得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象作下列变换,其中正确的变换是( )
的图象作下列变换,其中正确的变换是( )
A.先纵坐标不变,横坐标缩短原来的![]() 再按向量(
再按向量(![]() )平移
)平移
B.先纵坐标不变,横坐标缩短原来的![]() 再按向量(
再按向量(![]() )平移
)平移
C.先按向量(![]() )平移,再纵坐标不变,横坐标缩短原来的
)平移,再纵坐标不变,横坐标缩短原来的![]()
D.先按向量(![]() )平移,再纵坐标不变,横坐标缩短原来的
)平移,再纵坐标不变,横坐标缩短原来的![]()
10.已知x、y为正实数,且x,a1,a2,y成等差数列,x,b1,b2,y成等比数列,则![]() 的取值范围是( )
的取值范围是( )
A.R B.(0,4] C.[4,+![]() ) D. (-
) D. (-![]() ,0)
,0) ![]() [4,+
[4,+![]() )
)
11.过原点的直线与直x-y+8=0的夹角等于30°,则直线方程:( )
A. x=y B.x-2y= 0 C . x=0或x=y D. y=0或x-2y= 0
12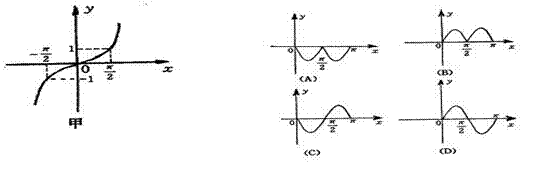 .已知函数
.已知函数![]() 图象如图甲,则
图象如图甲,则![]() 在区间[0,
在区间[0,![]() ]上大致图象是( )
]上大致图象是( )
二、填空题:本大题共5个小题,每小题4分,共20分。
13. 已知实数![]() 、
、![]() 满足约束条件
满足约束条件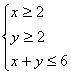 ,则
,则![]() 的最大值为_______.
的最大值为_______.
14.已知向量a=
(6,2),b = (一4,![]() ),直线m过点A(3,1)且与向量a+2b平行,则直线m的斜截式方程为_______ ______________________.
),直线m过点A(3,1)且与向量a+2b平行,则直线m的斜截式方程为_______ ______________________.
15.若![]() ,且
,且![]() ,则
,则![]() .
.
16.给出下列命题:
① 若直线x +ay-a=0与直线 ax-(2a-3)y-1=0互相垂直,则a=2;
② 若关于x的不等式x+1 -x-2 > a有实数解,则a<3;
③ 把函数y = sin2x-![]() cos2x的图象向左平移
cos2x的图象向左平移![]() 个单位,得出函数y=2sin2x的图象;
个单位,得出函数y=2sin2x的图象;
④ 若f(x)=3sin(![]() )对任意x都有f(
)对任意x都有f(![]() +x)=f(-x),则f (
+x)=f(-x),则f (![]() )的值为3 或-3.
)的值为3 或-3.
其中正确命题的序号是_________________ (把你认为正确的都填上).
三解答题(本大题共6个小题,共76分。)
17.(本小题满分12分)
![]()
(Ⅰ)求![]() 的最小正周期(6分) (Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,
的最小正周期(6分) (Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,![]() 求b,c的长(6分)
求b,c的长(6分)
18.(本小题满分12分)
已知![]() 是等差数列,其前n项和为Sn,已知
是等差数列,其前n项和为Sn,已知![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() 证明
证明![]() 是等比数列,并求其前n项和Tn.
是等比数列,并求其前n项和Tn.
19. (本小题满分12分)
甲、乙两人在罚球线投球命中的概率分别为![]() ,投中得1分,投不中得0分
,投中得1分,投不中得0分
(Ⅰ)甲、乙两人在罚球线各投球一次,求这两次投球中至少一次命中的概率;
(Ⅱ)甲、乙两人在罚球线各投球二次,求两人得分之和![]() 的分布列和数学期望
的分布列和数学期望
20.(本小题满分12分)
过定点A (2,1)任作两条互相垂直的直线l1和l2,设l1和l2分别与x轴、y轴相交于M、N两点.
(I) 求线段MN的中点P的轨迹C的方程;
(Ⅱ) 设原点为O,若点Q在轨迹C上,求OQ的最小值
21.(本小题满分12分)
设a>0为常数,函数![]() .
.
(I)求证:当x>2时,![]() ;
;
(Ⅱ) 求关于x的不等式f (x)>1的解集.
22.(本小题满分14分)
已知函数![]()
数列{a n}满足a n= f(n) (n∈N*)·
(I) 求数列{a n}的通项公式;
(Ⅱ) 设x轴、直线x=a与函数y=f(x)的图像所围成的封闭图形的面积为S(a) (a≥0),求S (n)-S (n一1) (n∈N*)关于n的表达式;
(Ⅲ) 在集合M={NN=2k,k∈Z,且1000≤k<1500}中,是否存在正整数N,使得不等式 a n一1005>S (n)-S(n一1) 对一切n>N恒成立?若存在,则这样的正整数N共有多少个?并求出满足条件的最小的正整数N;若不存在,请说明理由.