数列
1.（1）一般形式：
(2)通项公式：
(3)前n项和：
2.等差数列
(1)定义：
(2)通项公式：
推广：
(3)前n项和公式：
(4)性质
①
②
特别地：
③ 奇数项
偶数项
所以有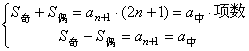
所以有
④
则有
3.等比数列
(1)定义：
(2)通项公式：
(3)前n项和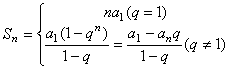
(4)性质：
①
②
特别地，
③
， 
，
则
4.数列通项
(1)等差，等比数列的通项
(2)
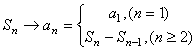
(3)迭加累加 ，迭乘累乘
，
，
，
………， ………，
，
，
注：
5.数列的求和
(1)等差与等比数列
(2)裂项相消法： 
(3)错位相减法：
, 
所以有
（4）通项分解法：
6.(1)
(2)
7.递推数列：
(1)能根据递推公式写出数列的前n项
(2)由
解题思路：利用
变化（1）已知
(2)已知
不等式
1、实数的大小顺序与运算性质之间的关系：
2、不等式的性质：
（1）
（反对称性）
（2）
（传递性）
（3）
，故
（移项法则的依据0
推论：
（同向不等式相加）
（4）
，
推论1：
推论2：
推论3：
3、常用的基本不等式和重要的不等式
（1）
当且仅当
（2）
（3）
，则
注：
（4）
4、最值定理
设
（1）如积
（2）如积
即；积定和最小，和定积最大。
注；运用最值定理求最值的三要素：一正二定三相等
5、不等式的证明方法
（1）比较法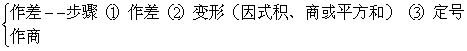
（2）综合法——由因导果
（3）分析法——执果索因
一般地常用分析法探索证题途径，然后用综合法
6、解不等式
（1）一元一次不等式 
①
②
（2）一元二次不等式 
第一册P39
判别式 
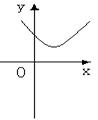
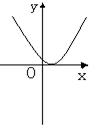
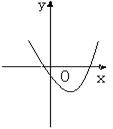二次函数
的图象
一元二次方程 相异实根 相等实根 没有实根
的根 
解集
R
解集
注：
解集为R，（ 对
恒成立）
则（Ⅰ）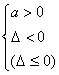
（Ⅱ）若二次函数系数含参数且未指明不为零时，需验证
若解集为R呢？
如：关于x的不等式
对恒成立，则
的取值范围
。
略解（Ⅰ）
（Ⅱ）
又如南通市二模22题
（3）绝对值不等式
（一）零点分段讨论
（二）公式法：
（4）高次不等式——序轴标根法
（5）分式不等式——序轴标根法
步骤：①形式：
②首项系数符号>0——标准式
若系数含参数时，须判断或讨论系数
，化负为正
③判断或比较根的大小。
7、（1）
（Ⅰ）基本不等式
（Ⅱ）
（2）含绝对值的不等式性质
统计
1.平均数（又称期望值）
设数据
，则
（1）
（2）设
， 
，………
,则
（3）
2.方差
衡量数据波动大小
（
较小）
（数据较小）
（数据较大）
--------标准差
3.抽样方法
(1)简单随机抽样：概率
其中n为样本容量， N为个体总数
(2)分层抽样：
其中n为样本容量， N为个体总数
n1为分层样本容量， N1为分层个体总数