普通高等学校春季招生考试高三数学卷
第Ⅰ卷
参考公式：
三角函数的积化和差公式 正棱台、圆台的侧面积公式
S 台侧=
其中 
、c 分别表示上下底面周长
表示斜高或母线长
球的体积公式
V锥
表示R表示球的半径
第I卷
一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
（1）
的共轭复数是
A．
B．
C．
D．
（2）函数
的图象是
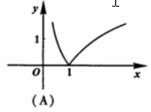
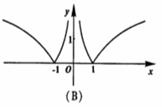
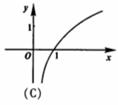
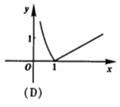
（3）有如下三个命题：
①分别在两个平面内的两条直线—定是异面直线；
②垂直于同一个平面的两条直线是平行直线；
③过平面。的一条斜线有一个平面与平面。垂直．
其中正确命题的个数为
A．0 B．1 C．2 D．3
（4）如果函数
的最小正周期是
，且当
时取得最大值，那么
A．
B．
C．
D．
（5）设
．“
”是“曲线
为椭圆”的
A．充分非必要条件 B．必要非充分条件
C．充分必要条件 D．既非充分又非必要条件
（6）已知双曲线的两个焦点为
，
，
是此双曲线上的一点，且
，
，则该双曲线的方程是
A．
B．
C．
D． 
（7）在
中，已知
，那么一定是
A．直角三角形 B．等腰三角形 C．等腰直角三角形 D．正三角形
（8）若不等式
对于任意正整数n恒成立，则实数
的取值范围是
A．
B．
C．
D．
第Ⅱ卷
二、填空题：本大题共6小题，每小题5分，共30分.把答案填在题中横线上.
（9）
．
（10）已知
，那么
的值为 ，
的值为 ．
（11）若圆
与直线
相切，且其圆心在
轴的左侧，则m的值为 ．
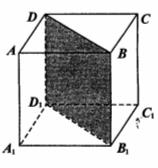（12）如图，正方体
的棱长为．将该正方体沿对角面
切成两块，再将这两块拼接成一个不是正方体的四棱柱，那么所得四棱柱的全面积为 ．
（13）从—1，０，1，2这四个数中选三个不同的数作为函数
的系数，可组成不同的二次函数共有 个，其中不同的偶函数共有 个(用数字作答)．
（14）若关于
的不等式
的解集为
，则实效
的取值范围是 ；若关于
的不等式
的解集不是空集，则实数的取值范围是 ．
三．解答题：本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步聚
(15)(本小题满分12分)
记函数
的定义域为集合M，函数
的定义域为集合
．求
（Ⅰ）集合M，；
（Ⅱ）集合
．
(16)(本小题满分14分)
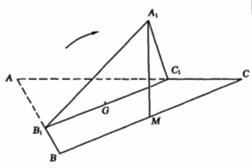如图，正三角形ABC的边长为3，过其中心G作BC边的平行线，分别交AB，AC于
．将
沿
折起到
的位置，使点
在平面
上的射影恰是线段BC的中点M．求
（Ⅰ）二面角
的大小；
（Ⅱ）异面直线
与
所成角的大小(用反三角函数表示)．
(17)(本小题满分14分)
已知
是等比数列，
；
是等差数列，
（Ⅰ）求数列的通项公式；
（Ⅱ）求数列的前
项和
的公式；
（Ⅲ）设
，
其中n＝1，2，…，试比较
与
的大小，并证明你的结论
(18)(本小题满分14分)
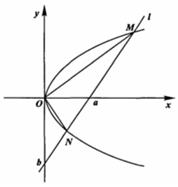如图，Ｏ为坐标原点，直线在轴和
轴上的截距分别是和
(
)，且交抛物线
于
，
两点．
（Ⅰ）写出直线的截距式方程；
（Ⅱ）证明：
（Ⅲ）当
时，求
的大小
(19)(本小题满分13分)
经过长期观测得到：在交通繁忙的时段内，某公路段汽车的车流量(千辆／小时)与汽车的平均速度
／(千米／小时)之间的函数关系为
（Ⅰ）在该时段内，当汽车的平均速度为多少时，车流量最大?最大车流量为多少? (精确到0．1千辆／小时)
（Ⅱ）若要求在该时段内车流量超过10千辆／小时，则汽车的平均速度应在什么范围内?
(20)(本小题满分13分)
现有一组互不相同且从小到大排列的数据：
其中
．为提取反映数据间差异程度的某种指标，今对其进行如下加工：记
，
，
作函数
，使其图象为逐点依次连接点
的折线．
（Ⅰ）求
和
的值；
（Ⅱ）设
的斜率为
，判断
的大小关系；
（Ⅲ）证明：当
时，
；
（Ⅳ）求由函数y=x与的图象所围成图形的面积(用
表示)．
普通高等学校春季招生考试
数学参考答案
一．选择题：本大题主要考查基本知识和基本技能．每小题5分，满分40分．
(1)D (2)A (3)C (4)A (5)B (6)C (7)B (8)A
二．填空题：本大题主要考查基本知识和基本运算．每小题5分，满分30分．
(9)
(10)
(11)
(12)
(13)
(14) 
三．解答题：本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤
(15)本小题主要考查集合的基本知识，考查逻辑思维能力和运算能力．满分12分．
解：（Ⅰ）
；
（Ⅱ）
，
(16)本小题主要考查直线与平面的位置关系等基本知识，考查空间想象能力，逻辑思维能力和运算能力．满分14分．
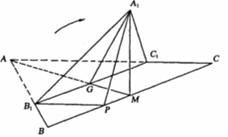
解：（Ⅰ）连接AM，
∵Ｇ是正三角形ABC的中心．且Ｍ为ＢC的中点，
∴Ａ，Ｇ，Ｍ三点共线，AM⊥BC．
∵∥BC，
∴⊥AM于Ｇ，即GM⊥，
⊥，
∴
是二面角的平面角．
∵点在平面上的射影为Ｍ，
∴
，
．
在Rt
中，由
得
，即二面角的大小是
．
(Ⅱ)过
作
的平行线交BC于Ｐ，则
等于异面直线与所成的角．
由
是平行四边形得
，PM=BM－BP＝，
．
∵
⊥面于Ｍ，
∴⊥BC，
．
在
中，
在
中，
在
中，由余弦定理得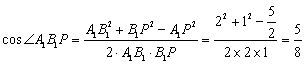
∴异面直线与所成角的大小为
(17)本小题主要考查等差数列、等比数列等基本知识，考查逻辑思维能力，分析问题和解决问题的能力．满分14分．
解：（Ⅰ）设的公比为
，由
得
当
时，
，这与
矛盾，故舍去；
当
时，
，故符合题意．
设数列的公差为d，由
得
又，解得
，所以
．
(Ⅱ)
(Ⅲ) 
组成以3d为公差的等差数列，所以
组成以2d为公差的等差数列，
，
所以
所以，对于正整数n，当
时，
；当
时，
；当
时，
．
(18)本小题主要考查直线、抛物线等基本知识，考查运用解析几何的方法分析问题和解决问题的能力．满分14分。
（Ⅰ）解：直线的截距式方程为
①
(Ⅱ)证明：由①及
消去可得
②
点Ｍ，N的纵坐标
为②的两个根，故
，
．
所以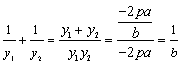
(Ⅲ) 解：设直线OM，ON的斜率分别为
，则
当时，由(Ⅱ)知
，
由
，
相乘得
，则
因此
所以
，即
．
(19)本小题主要考查函数、不等式等基本知识，考查应用数学知识分析问题和解决问题的能力．满分13分．
解：（Ⅰ）依题意，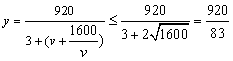
，当且仅当
，即=40时，等号成立，
所以
(千辆／小时)．
(Ⅱ)由条件得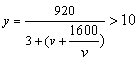
，整理得
，即
解得 25<<64．
答：当=40千米／小时时，车流量最大，最大车流量约为11．1千辆／小时．如果要求在该时段内车流量超过10千辆／小时，则汽车的平均速度应大于25千米／小时且小于64千米／小时．
(20)本小题主要考查函数、不等式等基本知识，考查逻辑思维能力、分析问题和解决问题的能力．满分13分．
（Ⅰ）解：
，
(Ⅱ)解：
，
因为
，所以
．
(Ⅲ)证明：由于
的图象是连接各点的折线，要证明，只需证明
（
1，2，3，4)．
事实上，当
时，
下面证明．
证法一：对任何n(n＝1，2，3，4)，5(
)＝
≤
所以
证法二：对任何n(n＝1，2，3，4)，
当
时，
当
时，
综上．
(Ⅳ)解：设
为[0，1]上折线与轴及直线
所围成图形的面积，则
直线
与折线所围成图形的面积为