普通高等学校春季招生考试数学卷2
数 学 试 卷
考生注意：1.答卷前，考生务必将姓名、高考座位号、校验码等填写清楚.
|
一. 填空题（本大题满分48分）本大题共有12题，只要求直接
填写结果，每题填对得4分，否则一律得零分.
1. 方程
的解集是
.
2. 
.
3. 若
，且
，则
.
4. 函数
的反函数
.
5. 在△
中，若
，
，则
.
6. 某班共有40名学生，其中只有一对双胞胎，若从中一次随机抽查三位学生的作业，则
这对双胞胎的作业同时被抽中的概率是 (结果用最简分数表示).
7. 双曲线
的焦距是
.
8. 若
，且
，则
.
9. 设数列
的前
项和为
（
）. 关于数列有下列三个命题：
（1）若既是等差数列又是等比数列，则
；
（2）若
，则是等差数列；
（3）若
，则是等比数列.
这些命题中，真命题的序号是 .
10. 若集合
，
，则
= .
11. 函数
的值域是
.
12. 已知函数
，数列
的通项公式是
（），当
取得最小值时， .
|
四个结论，其中有且只有一个结论是正确的，必须把正确结论的
代号写在题后的圆括号内，选对得 4分，否则一律得零分.
13. 已知直线
及平面
，下列命题中的假命题是
（A）若
，
，则
. （B）若
，
，则
.
（C）若
，，则. （D）若
，，则.
[答] ( )
14. 在△中，若
，则△是
（A）直角三角形. （B）等边三角形.
（C）钝角三角形. （D）等腰直角三角形.
[答] ( )
15. 若
是常数，则“
”是“对任意
，有
”
的
（A）充分不必要条件. （B）必要不充分条件.
（C）充要条件. （D）既不充分也不必要条件.
[答] ( )
16. 设函数
的定义域为
，有下列三个命题：
（1）若存在常数
，使得对任意，有
，则
是函数的最大值；
（2）若存在
，使得对任意，且
，有
，则
是函数
的最大值；
（3）若存在，使得对任意，有
，则是函数的最大值.
这些命题中，真命题的个数是
（A）0个. （B）1个. （C）2个. （D）3个.
[答] ( )
三．解答题（本大题满分86分）本大题共有6题，解答下列各题必须写出必要的步骤.
|
已知
是复数，
均为实数（
为虚数单位），且复数
在复平面上对应的点在第一象限，求实数
的取值范围.
[解]
|
已知
是方程
的两个根中较小的根，求
的值.
[解]
|
第2小题满分8分.
已知正三棱锥
的体积为
，侧面与底面所成的二面角的大小为
.
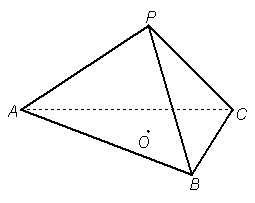（1）证明：
；
（2）求底面中心
到侧面的距离.
[证明]（1）
[解]（2）
|
第2小题满分8分.
某市2004年底有住房面积1200万平方米，计划从2005年起，每年拆除20万平方米的旧住房. 假定该市每年新建住房面积是上年年底住房面积的5%.
（1）分别求2005年底和2006年底的住房面积 ；
（2）求2024年底的住房面积.（计算结果以万平方米为单位，且精确到0.01）
[解]（1）
（2）
|
第2小题满分6分，第3小题满分7分.
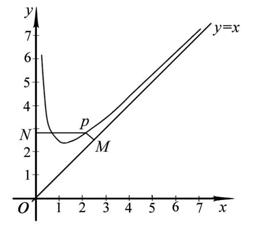已知函数
的定义域为
，且
. 设点
是函数图象上的任意一点，过点分别作直线
和
轴的垂线，垂足分别为
.
（1）求的值；
（2）问：
是否为定值？若是，则求出该定值，若不是，则说明理由；
（3）设为坐标原点，求四边形
面积的最小值.
[解]（1）
（2）
（3）
|
第2小题满分8分. 第3小题满分5分.
（1）求右焦点坐标是
，且经过点
的椭圆的标准方程；
（2）已知椭圆
的方程是
. 设斜率为
的直线
，交椭圆于
两点，
的中点为. 证明：当直线平行移动时，动点在一条过原点的定直线上；
（3）利用（2）所揭示的椭圆几何性质，用作图方法找出下面给定椭圆的中心，简要写出作图步骤，并在图中标出椭圆的中心.
[解]（1）
[证明]（2）
[解]（3）
普通高等学校春季招生考试
数 学 试 卷
参考答案及评分标准
说明
1.本解答列出试题的一种或几种解法,如果考生的解法与所列解法不同,可参照解答中评分标准的精神进行评分.
2.评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅,当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解答未改变这一题的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过后面部分应给分数之半,如果有较严重的概念性错误,就不给分.
3.第17题至第22题中右端所注的分数,表示考生正确做到这一步应得的该题的累加分数.
4.给分或扣分均以1分为单位.
答案及评分标准
一．（第1至12题）每一题正确的给4分，否则一律得零分.
1. 
. 2. 0. 3. 
. 4. 
.
5. 16. 6.
. 7. 
. 8. 11.
9. （1）、（2）、（3）. 10.
.
11. 
. 12. 110
二．（第13至16题）每一题正确的给4分，否则一律得零分.
| 题 号 | 13 | 14 | 15 | 16 |
| 代 号 | D | B | A | C |
三．（第17至22题）
17. [解] 设
，
，由题意得 
.
…… 2分
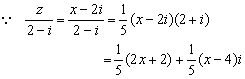
由题意得 
.
…… 6分
∴ 
.
∵ 
，
…… 9分
根据条件，可知
，解得 
，
∴ 实数的取值范围是
.
…… 12分
18. [解] ∵ 是方程
的较小根，
∴ 方程的较大根是
.
∵ +=
，即
∴ 
.
…… 5分
解得 
，或
.
…… 8分
当
时，
，
；
当
时，
，
，不合题意.
∴ 
.
…… 12分
19. [证明]（1）取
边的中点
，连接
、
，
则
，
，故
平面
.
…… 4分
∴ .
…… 6分
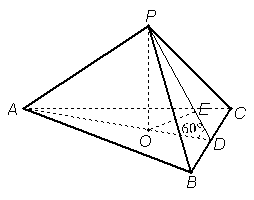[解]（2）如图， 由（1）可知平面
平面，则
是侧面与底面所成二面角的平面角.
过点作
为垂足，则
就是点到侧面的距离.
…… 9分
设为
，由题意可知点在上，
∴ 
，
.
, …… 11分
∴ 
，
∵ 
，∴ 
.
即底面中心到侧面的距离为3.
…… 14分
20. [解]（1）2005年底的住房面积为
（万平方米）,
2006年底的住房面积为
（万平方米）
∴ 2005年底的住房面积为1240万平方米，2006年底的住房面积约为1282万平方米. …… 6分
（2）2024年底的住房面积为
…… 10分
（万平方米）
∴ 2024年底的住房面积约为2522.64万平方米. …… 14分
21. [解]（1）∵ 
，∴ 
.
…… 3分
（2）设点的坐标为
，则有
，
，
由点到直线的距离公式可知：
，
故有
，即为定值，这个值为1.
…… 9分
（3）由题意可设
，可知
.
∵ 
与直线垂直，∴ 
，即 
，解得
，又，∴ 
.
∴
，
，
∴ 
，
当且仅当
时，等号成立.
∴ 此时四边形面积有最小值
.
…… 16分
22. [解]（1）设椭圆的标准方程为，
，
∴ 
，即椭圆的方程为
，
∵ 点（
）在椭圆上，∴ 
，
解得 
或
（舍），
由此得
，即椭圆的标准方程为
. …… 5分
（2）设直线
的方程为
，
…… 6分
与椭圆的交点
(
)、
(
)，
则有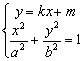
，
解得 
，
∵ 
，∴ 
，即 
.
则 
，
∴ 
中点的坐标为
.
…… 11分
∴ 线段的中点在过原点的直线 
上.
…… 13分
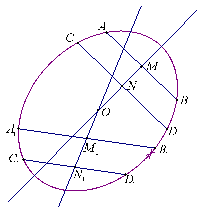（3）如图，作两条平行直线分别交椭圆于、和
，并分别取、
的中点
，连接直线
；又作两条平行直线（与前两条直线不平行）分别交椭圆于
、
和
，并分别取
、
的中点
，连接直线
，那么直线和的交点即为椭圆中心.
…… 18分