普通高等学校招生全国统一考试安数学卷
数学
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.第I卷1至2页.第II卷3至9页.共150分.考试时间120分钟.
第I卷(选择题共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)设集合A和B都是自然数集合N,映射![]() 把集合A中的元素
把集合A中的元素![]() 映射到集合B 中的元素
映射到集合B 中的元素![]() ,则在映射
,则在映射![]() 下,象20的原象是
下,象20的原象是
(A) 2 (B) 3 (C) 4 (D) 5
(2)在复平面内,把复数![]() 对应的向量按顺时针方向旋转
对应的向量按顺时针方向旋转![]() ,所得向量对应的复数是
,所得向量对应的复数是
(A) 2![]() (B)
(B)
![]() (C)
(C)
![]() (D)
3
(D)
3![]()
(3)一个长方体共一顶点的三个面的面积分别是![]() ,
,![]() ,
,![]() ,这个长方体对角线的长是
,这个长方体对角线的长是
(A) 2![]() (B) 3
(B) 3![]() (C)
6 (D)
(C)
6 (D)
![]()
(4)已知![]() ,那么下列命题成立的是
,那么下列命题成立的是
(A)若![]() 、
、![]() 是第一象限角,则
是第一象限角,则![]()
(B)若![]() 、
、![]() 是第二象限角,则
是第二象限角,则![]()
(C)若![]() 、
、![]() 是第三象限角,则
是第三象限角,则![]()
(D)若![]() 、
、![]() 是第四象限角,则
是第四象限角,则![]()
(5)函数![]() 的部分图象是
的部分图象是
|
|
(6)《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过800元的部分不必纳税,超过800元的部分为全月应纳税所得额.此项税款按下表分段累进计算:
| 全月应纳税所得额 | 税率 |
| 不超过500元的部分 | 5% |
| 超过500元至2000元的部分 | 10% |
| 超过2000元至5000元的部分 | 15% |
| … | … |
某人一月份应交纳此项税款26.78元,则他的当月工资、薪金所得介于
(A) 800~900元 (B) 900~1200元
(C) 1200~1500元 (D) 1500~2800元
(7)若![]() ,P=
,P=![]() ,Q=
,Q=![]() ,R=
,R=![]() ,则
,则
(A) R![]() P
P![]() Q (B)
P
Q (B)
P![]() Q
Q ![]() R
R
(C) Q ![]() P
P![]() R (D)
P
R (D)
P ![]() R
R![]() Q
Q
(8)以极坐标系中的点![]() 为圆心,1为半径的圆的方程是
为圆心,1为半径的圆的方程是
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
(9)一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
(10)过原点的直线与圆![]() 相切,若切点在第三象限,则该直线的方程是
相切,若切点在第三象限,则该直线的方程是
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
(11)过抛物线![]() 的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是
的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是![]() 、
、![]() ,则
,则![]() 等于
等于
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
|
|
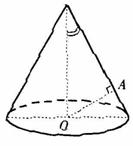
(12)如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转 一 周所得曲面将圆锥分成体积相等的两部分,则母线与轴的夹角为
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
第II卷(非选择题共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线.
(13)乒乓球队的10名队员中有3名主力队员,派5名参加比赛.3名主力队员要安排在第一、三、五位置,其余7名队员选2名安排在第二、四位置,那么不同的出场安排共有_____种(用数字作答).
(14)椭圆![]() 的焦点为
的焦点为![]() 、
、![]() ,点P为其上的动点,当
,点P为其上的动点,当![]() 为钝角时,点P 横坐标的取值范围是________.
为钝角时,点P 横坐标的取值范围是________.
 |
(15)设
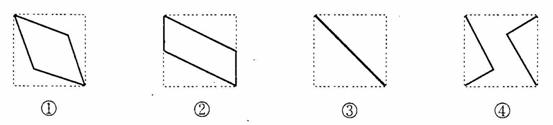
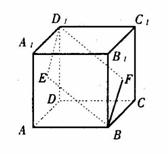
(16)如图,E、F分别为正方体的面![]() 、面
、面![]() 的中心,则四边形
的中心,则四边形![]() 在该正方体的面上的射影可能 是_______.(要求:把可能的图的序号都填上)
在该正方体的面上的射影可能 是_______.(要求:把可能的图的序号都填上)
|
|
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
(17)(本小题满分12分)
已知函数![]() ,
,![]() .
.
(I)当函数![]() 取得最大值时,求自变量
取得最大值时,求自变量![]() 的集合;
的集合;
(II)该函数的图象可由![]() 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
(18)(本小题满分12分)
|
|
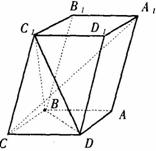
如图,已知平行六面体ABCD-![]() 的底面ABCD是菱形,且
的底面ABCD是菱形,且![]() =
=![]() =
=![]() =
=![]() .
.
(I)证明:![]() ⊥BD;
⊥BD;
(II)假定CD=2,![]() =
=![]() ,记面
,记面![]() 为
为![]() ,面CBD为
,面CBD为![]() ,求二面角
,求二面角 ![]() 的平面角的余弦值;
的平面角的余弦值;
(III)当![]() 的值为多少时,能使
的值为多少时,能使![]() 平面
平面![]() ?请给出证明.
?请给出证明.
(19)(本小题满分12分)
设函数![]() ,其中
,其中![]() .
.
(I)解不等式![]() ;
;
(II)求![]() 的取值范围,使函数
的取值范围,使函数![]() 在区间
在区间![]() 上是单调函数.
上是单调函数.
(20)(本小题满分12分)
(I)已知数列![]() ,其中
,其中![]() ,且数列
,且数列![]() 为等比数列,求常数
为等比数列,求常数![]() ;
;
(II)设![]() 、
、![]() 是公比不相等的两个等比数列,
是公比不相等的两个等比数列,![]() ,证明数列
,证明数列![]() 不是等比数列.
不是等比数列.
(21)(本小题满分12分)
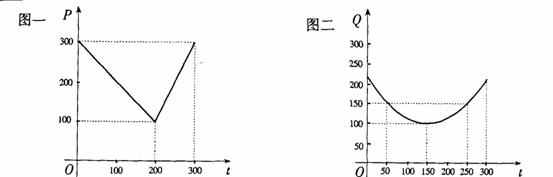
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示.
|
|
(Ⅰ)写出图一表示的市场售价与时间的函数关系式P=![]() ;
;
写出图二表示的种植成本与时间的函数关系式Q=![]() ;
;
(Ⅱ)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?
(注:市场售价和种植成本的单位:元/![]() kg,时间单位:天)
kg,时间单位:天)
(22)(本小题满分14分)
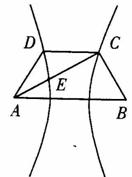
如图,已知梯形ABCD中![]() ,点E分有向线段
,点E分有向线段![]() 所成的比为
所成的比为![]() ,双曲线过C、D、E三点,且以A、B为焦点.当
,双曲线过C、D、E三点,且以A、B为焦点.当![]() 时,求双曲线离心率
时,求双曲线离心率![]() 的取值范围.
的取值范围.
普通高等学校招生全国统一考试
数学试题(理工农医类)参考解答及评分标准
一、选择题:本题考查基本知识和基本运算,每小题5分,满分60分.
(1)C (2)B (3)D (4)D (5)D (6)C
(7)B (8)C (9)A (10)C (11)C (12)D
二、填空题:本题考查基本知识和基本运算,每小题4分,满分16分.
(13)252 (14)-![]() (15)
(15)![]() (16)②③
(16)②③
三、解答题
(17)本小题主要考查三角函数的图象和性质,考查利用三角公式进行恒等变形的技能以及运算能力.满分12分.
解:(Ⅰ)
y=![]() cos2x+
cos2x+![]() sinxcosx+1
sinxcosx+1
=![]() (2cos2x-1)+
(2cos2x-1)+![]() +
+![]() (2sinxcosx)+1
(2sinxcosx)+1
=![]() cos2x+
cos2x+![]() sin2x+
sin2x+![]() =
=![]() (cos2x·sin
(cos2x·sin![]() +sin2x·cos
+sin2x·cos![]() )+
)+![]()
=![]() sin(2x+
sin(2x+![]() )+
)+![]() ——6分
——6分
y取得最大值必须且只需
2x+![]() =
=![]() +2kπ,k∈Z,
+2kπ,k∈Z,
即 x=![]() +kπ,k∈Z.
+kπ,k∈Z.
所以当函数y取得最大值时,自变量x的集合为
{xx=![]() +kπ,k∈Z
}
——8分
+kπ,k∈Z
}
——8分
(Ⅱ)将函数y=sinx依次进行如下变换:
(i)把函数y=sinx的图象向左平移![]() ,得到函数y=sin(x+
,得到函数y=sin(x+![]() )的图象;
)的图象;
(ii)把得到的图象上各点横坐标缩短到原来的![]() 倍(纵坐标不变),得到函数y=sin(2x+
倍(纵坐标不变),得到函数y=sin(2x+![]() )的图象;
)的图象;
(iii)把得到的图象上各点纵坐标缩短到原来的![]() 倍(纵坐标不变),得到函数y=
倍(纵坐标不变),得到函数y=![]() sin(2x+
sin(2x+![]() )的图象;
)的图象;
(iv)把得到的图象向上平移![]() 个单位长度,得到函数y=
个单位长度,得到函数y=![]() sin(2x+
sin(2x+![]() )+
)+![]() 的图象;综上得到函数y=
的图象;综上得到函数y=![]() cos2x+
cos2x+![]() sinxcosx+1的图象.
——12分
sinxcosx+1的图象.
——12分
(18)本小题主要考查直线与直线、直线与平面的关系,逻辑推理能力,满分12分.
(Ⅰ)证明:连结A1C1、AC、AC和BD交于O,连结C1O.
∵ 四边形ABCD是菱形,
∴ AC⊥BD,BD=CD.
又∵∠BCC1=∠DCC1,C1C= C1C,
∴ △C1BC≌△C1DC
∴ C1B=C1D,
∵ DO=OB
∴ C1O⊥BD, ——2分
但AC⊥BD,AC∩C1O=O,
∴ BD⊥平面AC1,
又C1C![]() 平面AC1
平面AC1
∴ C1C⊥BD. ——4分
(Ⅱ)解:由(Ⅰ)知AC⊥BD,C1O⊥BD,
∴ ∠C1OC是二面角α—BD—β的平面角.
在△C1BC中,BC=2,C1C=![]() ,∠BCC1=60º,
,∠BCC1=60º,
∴ C1B2=22+(![]() )2-2×2×
)2-2×2×![]() ×cos60º=
×cos60º=![]() ——6分
——6分
∵ ∠OCB=30º,
∴ OB=![]() BC=1.
BC=1.
∴C1O2= C1B2-OB2=![]() ,
,
∴ C1O=![]() 即C1O= C1C.
即C1O= C1C.
作 C1H⊥OC,垂足为H.
∴ 点H是OC的中点,且OH=![]() ,
,
所以cos∠C1OC=![]() =
=![]() .
——8分
.
——8分
(Ⅲ)当![]() =1时,能使A1C⊥平面C1BD
=1时,能使A1C⊥平面C1BD
证明一:
∵ ![]() =1,
=1,
∴ BC=CD= C1C,
又∠BCD=∠C1CB=∠C1CD,
由此可推得BD= C1B = C1D.
∴ 三棱锥C-C1BD是正三棱锥. ——10分
设A1C与C1O相交于G.
∵ A1 C1∥AC,且A1 C1∶OC=2∶1,
∴ C1G∶GO=2∶1.
又C1O是正三角形C1BD的BD边上的高和中线,
∴ 点G是正三角形C1BD的中心,
∴ CG⊥平面C1BD.
即A1C⊥平面C1BD. ——12分
证明二:
由(Ⅰ)知,BD⊥平面AC1,
∵ A1 C![]() 平面AC1,∴BD⊥A1 C.
——10分
平面AC1,∴BD⊥A1 C.
——10分
当![]() =1时,平行六面体的六个面是全等的菱形,
=1时,平行六面体的六个面是全等的菱形,
同BD⊥A1 C的证法可得BC1⊥A1C,
又BD⊥BC1=B,
∴ A1C⊥平面C1BD. ——12分
(19)本小题主要考查不等式的解法、函数的单调性等基本知识,分类讨论的数学思想方法和运算、推理能力.满分12分.
解:(Ⅰ)不等式f(x) ≤1即
![]() ≤1+ax,
≤1+ax,
由此得1≤1+ax,即ax≥0,其中常数a>0.
所以,原不等式等价于
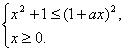
即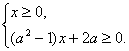 ——3分
——3分
所以,当0<a<1时,所给不等式的解集为{x0![]() };
};
当a≥1时,所给不等式的解集为{xx≥0}. ——6分
(Ⅱ)在区间[0,+∞]上任取x1、x2,使得x1<x2.
f(x1)-f(x2)=![]() -
-![]() -a(x1-x2)
-a(x1-x2)
=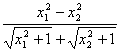 -a(x1-x2)
-a(x1-x2)
=(x1-x2)(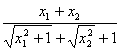 -a).
——8分
-a).
——8分
(ⅰ)当a≥1时
∵ 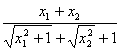 <1
<1
∴ 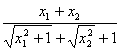 -a<0,
-a<0,
又x1-x2<0,
∴ f(x1)-f(x2)>0,
即f(x1)>f(x2).
所以,当a≥1时,函数f(x)在区间![]() 上是单调递减函数. ——10分
上是单调递减函数. ——10分
(ii)当0<a<1时,在区间![]() 上存在两点x1=0,x2=
上存在两点x1=0,x2=![]() ,满足f(x1)=1,f(x2)=1,即f(x1)=f(x2),所以函数f(x)在区间
,满足f(x1)=1,f(x2)=1,即f(x1)=f(x2),所以函数f(x)在区间![]() 上不是单调函数.
上不是单调函数.
综上,当且仅当a≤1时,函数f(x)在区间![]() 上是单调函数.
——12分
上是单调函数.
——12分
(20)本小题主要考查等比数列的概念和基本性质,推理和运算能力,满分12分.
解:(Ⅰ)因为{cn+1-pcn}是等比数列,故有
(cn+1-pcn)2=( cn+2-pcn+1)(cn-pcn-1),
将cn=2n+3n代入上式,得
[2n+1+3n+1-p(2n+3n)]2
=[2n+2+3n+2-p(2n+1+3n+1)]·[2n+3n-p(2n-1+3n-1)], ——3分
即[(2-p)2n+(3-p)3n]2
=[(2-p)2n+1+(3-p)3n+1][ (2-p)2n-1+(3-p)3n-1],
整理得![]() (2-p)(3-p)·2n·3n=0,
(2-p)(3-p)·2n·3n=0,
解得p=2或p=3. ——6分
(Ⅱ)设{an}、{bn}的公比分别为p、q,p≠q,cn=an+bn.
为证{cn}不是等比数列只需证![]() ≠c1·c3.
≠c1·c3.
事实上,![]() =(a1p+b1q)2=
=(a1p+b1q)2=![]() p2+
p2+![]() q2+2a1b1pq,
q2+2a1b1pq,
c1·c3=(a1+b1)(a1 p2+b1q2)= ![]() p2+
p2+![]() q2+a1b1(p2+q2).
q2+a1b1(p2+q2).
由于p≠q,p2+q2>2pq,又a1、b1不为零,
因此![]() c1·c3,故{cn}不是等比数列.
——12分
c1·c3,故{cn}不是等比数列.
——12分
(21)本小题主要考查由函数图象建立函数关系式和求函数最大值的问题,考查运用所学知识解决实际问题的能力,满分12分.
解:(Ⅰ)由图一可得市场售价与时间的函数关系为
f(t)=![]() ——2分
——2分
由图二可得种植成本与时间的函数关系为
g(t)=![]() (t-150)2+100,0≤t≤300.
——4分
(t-150)2+100,0≤t≤300.
——4分
(Ⅱ)设t时刻的纯收益为h(t),则由题意得
h(t)=f(t)-g(t)
即h(t)=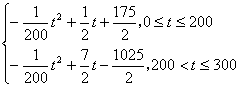 ——6分
——6分
当0≤t≤200时,配方整理得
h(t)=-![]() (t-50)2+100,
(t-50)2+100,
所以,当t=50时,h(t)取得区间[0,200]上的最大值100;
当200<t≤300时,配方整理得
h(t)=-![]() (t-350)2+100
(t-350)2+100
所以,当t=300时,h(t)取得区间[200,300]上的最大值87.5. ——10分
综上,由100>87.5可知,h(t)在区间[0,300]上可以取得最大值100,此时t=50,即从二月一日开始的第50天时,上市的西红柿纯收益最大. ——12分(22)本小题主要考查坐标法、定比分点坐标公式、双曲线的概念和性质,推理、运算能力和综合应用数学知识解决问题的能力,满分14分.
解:如图,以AB的垂直平分线为y轴,直线AB为x轴,建立直角坐标系xoy,则CD⊥y轴.
因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于x轴对称. ——2分
依题意,记A(-c,0),C(![]() ,h),E(x0, y0),其中c=
,h),E(x0, y0),其中c=![]() AB为双曲线的半焦距,h是梯形的高.
AB为双曲线的半焦距,h是梯形的高.
由定比分点坐标公式得
x0=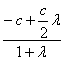 =
= ![]() ,
,
![]() .
.
设双曲线的方程为![]() ,则离心率
,则离心率![]() .
.
由点C、E在双曲线上,将点C、E的坐标和![]() 代入双曲线方程得
代入双曲线方程得
![]() ,
①
,
①
![]() . ②
——7分
. ②
——7分
由①式得 ![]() ,
③
,
③
将③式代入②式,整理得
![]() ,
,
故 ![]() .
——10分
.
——10分
由题设![]() 得,
得,![]() .
.
解得![]() .
.
所以双曲线的离心率的取值范围为![]() .
——14分
.
——14分