普通高等学校招生全国统一考试高考数学86

普通高等学校招生全国统一考试高考数学86

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。第Ⅰ卷1至2页，第Ⅱ卷3至4页，共4页。全卷共150分。考试用时120分钟。

第Ⅰ卷（选择题　共50分）

一、选择题:本大题共10小题，每小题5分，共50分散。在每个小题给出的四个选项中，只有一项是符合题目要求的。

1、集合P＝｛x」x²－16<0｝,Q＝｛x」x＝2n，nZ｝,则PQ＝

A.｛-2,2｝　　 B.｛－2，2，－4，4｝　　 C.｛2，0，2｝　　　D.｛－2，2，0，－4，4｝

2、已知非零向量a、b，若a＋2b与a－2b互相垂直，则

A. 　　　　　　　 B.　4　　　　　　  C. 　　　　　　　D. 2

3、已知＝，A∈（0，），则

A.　　　　　　  B．　　　　 C．　　　　　　  D．

4、在等比数列｛a_n｝中，a₁＝1，a₁₀＝3，则a₂a₃a₄a₅a₆a₇a₈a₉

A. 81　　　　　　  B.　27　　　　　　 C. 　　　　　　　D. 243

5、甲：A₁、A₂是互斥事件；乙：A₁、A₂是对立事件，那么

A. 甲是乙的充分但不必要条件　　　　B. 甲是乙的必要但不充分条件

C. 甲是乙的充要条件　　　　　　　  D. 甲既不是乙的充分条件，也不是乙的必要条件

6、关于直线m、n与平面与，有下列四个命题：

①若且，则；

②若且，则；

③若且，则；

④若且，则；

其中真命题的序号是

A．①②　　B．③④　　C．①④　　D．②③

7、设f(x)＝，则的定义域为

A. 　 B.(－4,－1)(1，4)　 C. (－2,－1)(1，2)　D. (－4,－2)(2，4)

8、在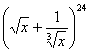的展开式中，x的幂的指数是整数的有

A. 3项　　　　　　  B. 4项　　　　　　　 C. 5项　　　　　　 D. 6项

9、设过点P（x，y）的直线分别与x轴的正半轴和y轴的正半轴交于A、B两点，若，则点P的轨迹方程是

A. 　　　　　　B.　

C. 　　　　　　D.

10、关于x的方程，给出下列四个命题：

①存在实数，使得方程恰有2个不同的实根；

②存在实数，使得方程恰有4个不同的实根；

③存在实数，使得方程恰有5个不同的实根；

④存在实数，使得方程恰有8个不同的实根；

其中假命题的个数是

A．0　　　　　　  B．1　　　　　　　　  C．2　　　　　　　　 D．3

第Ⅱ卷（非选择题　 共100分）

注意事项：

第Ⅱ卷用0.5毫米黑色的签字笔或黑色墨水钢笔直接答在答题卡上。答在试题卷上无效。

二、填空题：本大题共5小题，每小题5分，共25分，把答案填在答题卡相应位置上。

11、在ABC中，已知，b＝4，A＝30°，则sinB＝　　　　　  .

12．接种某疫苗后，出现发热反应的概率为0．80，现有5人接种了该疫苗，至少有3人出现发热反应的概率为　　　　  。（精确到0．01）

13、若直线y＝kx＋2与圆(x－2)²＋(y－3)²＝1有两个不同的交点，则k 的取值范围是　　　.

14、安排5名歌手的演出顺序时，要求某名歌手不第一个出场，另一名歌手不最后一个出场，不同排法的总数是　　　　　　  .(用数字作答)

15、半径为r的圆的面积S(r)＝r²,周长C(r)=2r，若将r看作(0，＋∞)上的变量，则(r²)`＝2r　1，

1式可以用语言叙述为：圆的面积函数的导数等于圆的周长函数。

对于半径为R的球，若将R看作(0，＋∞)上的变量，请你写出类似于1的式子：　　　　　　　　　　　　　  2

2式可以用语言叙述为：　　　　　　　　　　　　　　　　　　　  。

答案

一、选择题：1.C　2.D　3.A  4.A　5.B　6.D  7.B　8.C　9.D  10.A

二、填空题：11.　12.　0.94　　13. (0，)　 14.　78 

15.（R³）`＝4R²，球的体积函数的导数等于球的表面积函数。

三、解答题：本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤。

16、（本小题满分12分）

设向量a＝(sinx，cosx)，b＝(cosx，cosx)，x∈R，函数f(x)＝a·(a＋b).

（Ⅰ）求函数f(x)的最大值与最小正周期；

（Ⅱ）求使不等式f(x)≥成立的x的取值集。

点评：本小题主要考查平面向量数量积的计算方法、三角公式、三角函数的基本知识，以及运用三角函数的图像和性质的能力。

解：（Ⅰ）∵f(x)＝a·(a＋b)＝a·a＋a·b＝sin²x＋cos²x＋sinxcosx＋cos²x

＝1＋sin2x＋(cos2x＋1)＝＋sin(2x+)

∴f(x)的最大值为＋，最小正周期是＝

（Ⅱ）要使f(x)≥成立，当且仅当＋sin(2x+)≥，

即sin(2x+)≥02k≤2x+≤2k+k－≤x≤k+，kZ.

即f(x)≥成立的x的取值集合是｛k－≤x≤k+，kZ｝

17、（本小题满分12分）

某单位最近组织了一次健身活动，活动分为登山组和游泳组，且每个职工至多参加了其中一组。在参加活动的职工中，青年人占42.5％，中年人占47.5％，老年人占10％。登山组的职工占参加活动总人数的，且该组中，青年人占50％，中年人占40％，老年人占10％。为了了解各组不同的年龄层次的职工对本次活动的满意程度，现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本。试确定

（Ⅰ）游泳组中，青年人、中年人、老年人分别所占的比例；

（Ⅱ）游泳组中，青年人、中年人、老年人分别应抽取的人数。

点评：本小题主要考查分层抽样的概念和运算，以及运用统计知识解决实际问题的能力。

解：（Ⅰ）设登山组的人数为x，游泳组中，青年人、中年人、老年人各占比例分别为a、b、c，依题意，总人数为4x，游泳组人数为3x，则

，，

且a＋b＋c＝100％，将以上各式联立，解得

a＝40％，b＝50％，c＝10％.

故游泳组中，青年人、中年人、老年人各占比例分别为40％，50％和10％；

（Ⅱ）游泳组中，抽取的青年人数是200××40％＝60（人），抽取的中年人数是200××50％＝75（人），抽取的老年人数是200××10％＝15（人）。

18、（本小题满分12分）

如图，已知正三棱柱ABC-A₁B₁C₁的侧棱长和底面边长均为1，M是底面BC边上的中点，N是侧棱CC₁上的点，且CN＝2C₁N.

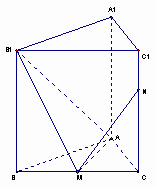（Ⅰ）求二面角B₁－AM－N的平面角的余弦值；

（Ⅱ）求点B₁到平面AMN的距离。

点评：本小题主要考查线面关系、二面角和点到平面距离的有关知识及空间想象能力以及推理运算能力。考查运用向量知识解决数学问题的能力。

解：（Ⅰ）因为点M是底面BC边上的中点，

所以AM⊥B₁M，AM⊥BB₁，则AM⊥平面B₁BCC₁，

从而，AM⊥B₁M ，AM⊥NM.

所以∠B₁M N是二面角B₁－AM－N的平面角。

又B₁M ＝,

MN＝,

连B₁N，B₁N＝.

在B₁M N中，由余弦定理得

cosB₁M N=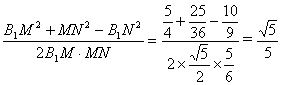

故所求二面角B₁－AM－N的平面角的余弦值为。

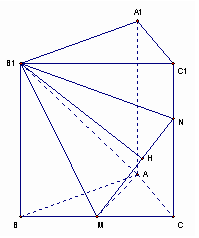
（Ⅱ）过点B₁在平面B₁BCC₁内作直线B₁H⊥MN　 ，H为垂足，

又AM⊥平面B₁BCC₁，所以AM⊥B₁H，

　　 所以，B₁H⊥平面AMN，故B₁即为B₁到平面AMN的距离。

在rtB₁HM中，B₁H＝B₁MsinB₁MH＝.

故点B₁到平面AMN的距离为1。　

19、（本小题满分12分）

设函数f(x)=x³+ax²+bx+c在x＝1处取得极值－2，试用c表示a和b，并求f(x)的单调区间。

点评：本小题主要考查导数的概念和计算，考查运用导数研究函数的性质的方法及推理和运算能力。

解：根据题意，得f(1)＝－2，f `(1)＝0，而f `(x)＝3x²+2ax+b.

则，解得

从而f `(x)=3x²+2cx－2c－3＝(3x＋2c＋3)(x－1)

令f `(x)＝0，得x₁＝1或x₂＝，由于x＝1是极值点，

所以3x+2c+3≠1，那么c≠－3.

当c<－3时，x₂>1＝x₁，则

在区间（－∞，1）上，f `(x)>0， f (x)为增函数；

在区间（1，）上，f `(x)<0，f (x)为减函数；

在区间（，＋∞）上，f `(x)>0，f (x)为增函数。

当c>－3时，x₂<1＝x₁，则

在区间（－∞，）上，f `(x)>0， f (x)为增函数；

在区间（，1）上，f `(x)<0，f (x)为减函数；

在区间（1，＋∞）上，f `(x)>0，f (x)为增函数。

20、（本小题13分）

设数列的前n项和为，点均在函数y＝3x－2的图像上。

（Ⅰ）求数列的通项公式；

（Ⅱ）设，是数列的前n项和，求使得对所有都成立的最小正整数m。

点评：点评：本小题考查二次函数、等差数列、数列求和、不等式等基础知识和基本的运算技能，考查分析问题的能力和推理能力。

解：（Ⅰ）依题意得，即S_n=3n²－2n.

当n≥2时，a_n＝S_n－S_n－1＝（3n²－2n）－＝6n－5.

当n＝1时，a₁＝S₁＝3×1²－2＝6×1－5，所以，a_n＝6n－5 （）

（Ⅱ）由（Ⅰ）得知＝＝，

故T_n＝＝＝（1－）.

因此，要使（1－）<（）成立的m,必须且仅须满足≤，即m≥10，所以满足要求的最小正整数m为10.

21、（本小题满分13分）

设分别为椭圆的左、右顶点，椭圆长半轴的长等于焦距，且为它的右准线。

（Ⅰ）、求椭圆的方程；

（Ⅱ）、设为右准线上不同于点（4，0）的任意一点，若直线分别与椭圆相交于异于的点，证明点在以为直径的圆内。

（此题不要求在答题卡上画图）

点评：本小题主要考查直线、圆和椭圆等平面解析几何的基础知识，考查综合运用数学知识进行推理运算的能力和解决问题的能力。

解：（Ⅰ）依题意得 a＝2c，＝4，解得a＝2，c＝1，从而b＝.

故椭圆的方程为 .

（Ⅱ）解法1：由（Ⅰ）得A（－2，0），B（2，0）.设M（x₀，y₀）.

∵M点在椭圆上，∴y₀＝（4－x₀²）.　　　　　　　　　　　 1

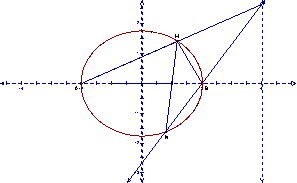又点M异于顶点A、B，∴－2<x₀<2，由P、A、M三点共线可以得

P（4，）.

从而＝（x₀－2，y₀），

＝（2，）.

∴·＝2x₀－4＋＝（x₀²－4＋3y₀²）.　　　2

将1代入2，化简得·＝（2－x₀）.

∵2－x₀>0，∴·>0，则∠MBP为锐角，从而∠MBN为钝角，

故点B在以MN为直径的圆内。

解法2：由（Ⅰ）得A（－2，0），B（2，0）.设M（x₁，y₁），N（x₂，y₂），

则－2<x₁<2，－2<x₂<2，又MN的中点Q的坐标为（，），

依题意，计算点B到圆心Q的距离与半径的差

－＝(－2）²＋（）²－[(x₁－x₂)²＋(y₁－y₂)²]

　　　　　　　　 ＝（x₁－2) (x₂－2)＋y₁y₁　　　　　　　　 　　3

又直线AP的方程为y＝，直线BP的方程为y＝，

而点两直线AP与BP的交点P在准线x＝4上，

∴，即y₂＝　　　　　　　　　　　 4

又点M在椭圆上，则，即　　　　5

于是将4、5代入3，化简后可得－＝.

从而，点B在以MN为直径的圆内。