高三数学综合练习二
一、选择题(每小题5分,共50分)
1.函数![]() 的定义域是(D)
的定义域是(D)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设集合![]() ,若
,若![]() ,则实数
,则实数![]() 的取值范围是(B)
的取值范围是(B)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.对于函数![]() ,下列结论正确的是(B)
,下列结论正确的是(B)
A.有最大值而无最小值 B.有最小值而无最大值
C.有最大值且有最小值 D.既无最大值又无最小值
4.已知映射![]() ,其中集合
,其中集合![]() ,集合B中元素都是A中元素在映射
,集合B中元素都是A中元素在映射![]() 下的像,且对任意的
下的像,且对任意的![]() ,在B中与它对应的元素是
,在B中与它对应的元素是![]() ,则集合B是( )
,则集合B是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.在下列函数中,定义域和值域不同的函数是(D)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.函数![]() 在闭区间
在闭区间![]() 上的最大值、最小值分别是(C)
上的最大值、最小值分别是(C)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
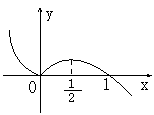 7.函数
7.函数![]() 的图象如右图所示,则当
的图象如右图所示,则当![]() 时,函数
时,函数![]() 的单调减区间是(A)
的单调减区间是(A)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.二次函数满足![]() ,又
,又![]() ,若在
,若在![]() 有最小值1,最大值3,则
有最小值1,最大值3,则![]() 的取值范围是(D)
的取值范围是(D)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.函数![]() 的图象与直线
的图象与直线![]() 相切,则
相切,则![]() 等于(B)
等于(B)
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
10.设数集![]() ,且M、N都是集合
,且M、N都是集合![]() 的子集,如果把
的子集,如果把![]() 叫做集合
叫做集合![]() 的“长度”,那么
的“长度”,那么![]() 的“长度”的最小值是(C)
的“长度”的最小值是(C)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(每小题5分,共20分)
11.函数![]() 的值域是
。[0,2]
的值域是
。[0,2]
12.已知![]() ,当
,当![]() 只有一个元素时,
只有一个元素时,![]() 的关系式是
。
的关系式是
。![]()
13.若![]() 成等比数列,则函数
成等比数列,则函数![]() 的图象与
的图象与![]() 轴的公共点有 个。0
轴的公共点有 个。0
14.若![]() 是偶函数,则
是偶函数,则![]() 。
。![]()
三、解答题(6小题,共80分)
15.(本小题满分12分)证明:![]() 在定义域内为减函数。
在定义域内为减函数。
(3。5模拟P41)
16.(本小题满分13分)定义在R上的奇函数![]() 有最小正周期2,且
有最小正周期2,且![]() 时,
时,![]() 。
。
(1)求![]() 在
在![]() 上的解析式;
上的解析式;
(2)判断![]() 在(0,1)上的单调性,并给予证明。
在(0,1)上的单调性,并给予证明。
(3。5模拟P29)
17.(本小题满分13分)已知定义域为R的函数![]() 是奇函数。
是奇函数。
(1)求![]() 的值;
的值;
(2)若对任意的![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围。
的取值范围。
(3。5模拟P57)
18.(本小题满分14分)已知函数![]() 的图象与
的图象与![]() 轴分别相交于A、B,
轴分别相交于A、B,![]() 分别是与
分别是与![]() 轴正半轴同方向的单位向量),函数
轴正半轴同方向的单位向量),函数![]() 。
。
(1)求![]() 的值;
的值;
(2)当![]() 满足
满足![]() 时,求函数
时,求函数![]() 的最小值。
的最小值。
(3。5模拟P53)
19.已知二次函数![]() 的定义域为R,
的定义域为R,![]() ,且在
,且在![]() 处(
处(![]() 为实数)取得最值,若
为实数)取得最值,若![]() 为一次函数,且
为一次函数,且![]()
(1)求![]() 解析式;
解析式;
(2)若![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围。
的取值范围。
(金P21。8)
20.(本小题满分14分)设![]() ,若
,若![]() ,求证:
,求证:
(1)方程![]() 有实根;
有实根;
(2)![]() ;
;
(3)设![]() 是方程
是方程![]() 的两个实根,则
的两个实根,则![]()
(06渐江20)