高三数学综合练习三
一、选择题（每小题5分，共50分）
1．已知集合
，则
的取值范围是（D）
A．[0，1]
B．
C．
D．
2．若
，则
等于（D）
A．0 B．2 C．8 D．16
3．已知
，则函数
的图象必定不经过（B）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
4．方程
的解集为M，方程
的解集为N，那么M与N 的关系是（A）
A．M=N
B．
C．
D．
5．函数
，则函数
是（A）
A．奇函数 B．偶函数 C．非奇非偶函数 D．既是奇函数又是偶函数
6．对于函数
，若
，则函数在区间
内（C）
A．一定有零点 B．一定没有零点
C．可能有两个零点 D．至多有一个零点
7．下列说法：①任取
都有
；②当
时，任取都有
；③
是增函数；④
的最小值为1；⑤在同一坐标系中，
与
的图象对称于
轴。其中正确的是（B）
A．①②④ B．④⑤ C．②③④ D．①⑤
8．已知函数
图象恒过点（2，0），则
的最小值为（B）
A．5
B．
C．4
D．
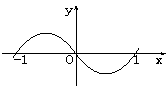
9．已知
的图象如图所示，今考虑
，则方程式
（A）
A．当
时，恰有一实根
B．当
时，恰有一实根
C．当
时，恰有一实根
D．当
时恰有一实根
10．已知是奇函数，且在
上是递减函数，在（0，1）上是单调增函数，则
的大小关系是（A）
A．
B．
C．
D．不确定
二、填空题（每小题5分，共20分）
11．若集合
，且
，那么集合P的子集个数有
个。8
12．关于
的方程
有负根，则实数的取值范围是
。
13．函数
的单调递增区间是
；其值域为
。
14．已知函数
满足：（1）对任意
，都有
；（2）
，写出一个同时满足这些条件的函数解析式
。（只要写出一个即可） 
三、解答题（6小题，共80分）
15．（本小题满分12分）已知二次函数满足
，且的最大值是8，试确定此二次函数的解析式。
16．（本小题满分13分）设
，且
，如果函数
在
上的最大值为14，求的值。
17．（本小题满分13分）某租赁公司拥有汽车100辆，当每辆车的月租金为3000元时，可全部租出。当每辆车的月租金增加50元时，未租出的车将会增加一辆，租出的车每辆每月需维护费150元，未租出的车每辆每月需要维护费50元。
（1）当每辆车的月租金定为3600元时，能租出多少辆车？
（2）当每辆车的月租金定为多少时，租赁公司的月收益最大？最大月收益是多少？
18．（本小题满分14分）定义在实数集上的函数，对任意
，有
，且
。
（1）求证：
；
（2）求证：
是偶函数；
（3）若存在常数
，使
。①求证对任意，有
成立；②试问函数是不是周期函数，如果是，找出它的一个周期；如果不是，请说明理由。
19．（本小题满分14分）已知函数的图象与函数
的图象关于点A（0，1）对称。
（1）求的解析式；
（2）若
，且
在区间
上为减函数，求实数的取值范围。
20．（本小题满分14分）已知函数
，点
是函数 图象上的任意两点，且线段
的中点P的横坐标为
。
（1）求证：点P的纵坐标为定值；
（2）在数列
中，若 
，求数列的前
项和
。