普通高等学校招生全国统一数学考试
数学（理工农医类）
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第1卷1至2页．第Ⅱ卷3至8页．共150分．考试时间120分钟．
第Ⅰ卷（选择题共60分）
注意事项：
1． 答第Ⅰ卷前，考生务必将自己的姓名、准考证号填写在试题卷指定地方．并将姓名、考试科目、准考证号用铅笔涂写在答题卡上．
2． 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号徐黑．如需改动，用橡皮擦干净后，再选涂其它答案．不能答在试题卷上．
3． 
考试结束，监考人员将本试卷和答题卡一并收回．
一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
（1）若
＞0，则
在
（A）第一、二象限 （B）第一、三象限 （C）第一、四象限 （D）第二、四象限
（2）过点A（1，—1）、B（—1，1）且圆心在直线x十y—2＝0上的圆的方程是
（A）
（B）
（C）
（D）
（3）设｛an｝是递增等差数列，前三项的和为12，前三项的积为48，则它的首项是
（A）1 （B）2 （C）4 （D）6
（4）若定义在区间（—1，0）内的函数
满足
＞0，则a的取值范围是
（A）
（B）
（C）
（D）
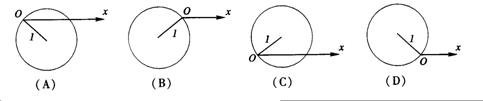
（5）极坐标方程
的图形是
（6）函数y＝x＋1
的反函数是
（A）y＝－arccos（x－1） （0≤x≤2） （B）y＝
－arccos（x－1） （0≤x≤2）
（C）y＝arccos（x－1） （0≤x≤2） （D）y＝＋arccos（x－1） （0≤x≤2）
（7）若椭圆经过原点，且焦点为F1（1，0），F2（3，0），则其离心率为
（A）
（B）
（C）
（D）
（8）若
，则
（A）a＜b （B）a＞b （C）ab＜1 （D）ab＞2
（9）在正三棱柱ABC—A1B1C1中，若AB＝
BB1，则AB1与C1B所成的角的大小为
（A）60° （B）90° （C）105° （D）75°
（10）设f （x）、g （x）都是单调函数，有如下四个命题：
①若f （x）单调递增，g （x）单调递增，则f （x）－g （x）单调递增；
②若f （x）单调递增，g （x）单调递减，则f （x）－g （x）单调递增；
③若f （x）单调递减，g （x）单调递增，则f （x）－g （x）单调递减；
④若f （x）单调递减，g （x）单调递减，则f （x）－g （x）单调递减．
其中，正确的命题是
（A）①③ （B）①④ （C）②③ （D）②④
（11）一间民房的屋顶有如图三种不同的盖法：①单向倾斜；②双向倾斜；②四向倾斜．记三种盖法屋顶面积分别为P1、P2、P3 ．
若屋顶斜面与水平面所成的角都是
，则
（A）P3＞P2＞P1 （B）P3＞P2＝P1 （C）P3＝P2＞P1 （D）P3＝P2＝P1
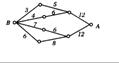（12）如图，小圆圈表示网络的结点，结点之间的连线表示它们有网
线相联．连线标注的数字表示该段网线单位时间内可以通过的最大信息量．现从结点A
向结点B传递信息，信息可以分开沿不同的路线同时传递．则单位时间内传递的最大信息量为
（A）26 （B）24 （C）20 （D）19
第Ⅱ卷（非选择题共90分）
注意事项：
1． 第Ⅱ卷共6页，用钢笔或圆珠笔将答案直接答在试卷上．
2． 答卷前将密封线内的项目填写清楚．
3． 座位号填写准考证号最末尾两位数．
二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．
（13）若一个圆锥的轴截面是等边三角形，其面积为
，则这个圆锥的侧面积是
．
（14）双曲线
的两个焦点为F1、F2，点P在双曲线上．若PF1⊥PF2，则点P到x轴的距离为
．
（15）设｛an｝是公比为q的等比数列，Sn是它的前n项和．若｛Sn｝是等差数列，则q＝ ．
（16）圆周上有2n个等分点（n＞1），以其中三个点为顶点的直角三角形的个数为 ．
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
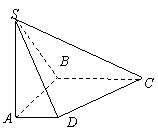（17）（本小题满分12分）
如图，在底面是直角梯形的四棱锥S—ABCD中，∠ABC＝90°，SA⊥面ABCD，SA＝AB＝BC＝1，AD＝
．
（Ⅰ）求四棱锥S—ABCD的体积；
（Ⅱ）求面SCD与面SBA所成的二面角的正切值．
（18）（本小题满分12分）
已知复数z1＝i （1—i ）3．
（Ⅰ）求arg z1及 z ；
（Ⅱ）当复数z满足 z ＝1，求 z—z1 的最大值．
（19）（本小题满分12分）
设抛物线
的焦点为F，经过点F的直线交抛物线于A、B两点，点C在抛物线的准线上，且BC∥x轴．证明直线AC经过原点O．
（20）（本小题满分12分）
已知i，m，n是正整数，且1＜i≤m＜n．
（Ⅰ）证明
；
（Ⅱ）证明
．
（21）（本小题满分12分）
从社会效益和经济效益出发，某地投入资金进行生态环境建设，并以此发展旅游产业．根据规划，本年度投入800万元，以后每年投入将比上年减少
．本年度当地旅游业收入估计为400万元，由于该项建设对旅游业的促进作用，预计今后的旅游业收入每年会比上年增加
．
（Ⅰ）设n年内（本年度为第一年）总投人为an万元，旅游业总收入为bn万元．写出an，bn的表达式；
（Ⅱ）至少经过几年旅游业的总收人才能超过总投入?
（22）（本小题满分12分）
设f （x）是定义在R上的偶函数。其图象关于直线y＝x对称，对任意x1，x2
，都有f （x1＋x2）＝f （x1）·f （x2），且f （
1 ）＝a＞0．
（Ⅰ）求
及
；
（Ⅱ）证明f （x）是周期函数；
（Ⅲ）记
，求
．
普通高等学校招生全国统一考试
数学（理工农医类）参考答案及评分标准
说明：
一．本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．
二．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答末改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．
三．解答右端所注分数，表示考生正确做到这一步应得的累加分数．
四．只给整数分数．选择题和填空题不给中间分．
一、选择题：本题考查基本知识和基本运算，每小题5分，满分60分．
（1）B （2）C （3）B （4）A （5）C （6）A
（7）C （8）A （9）B （10）C （11）D （12）D
二、填空题：本题考查基本知识和基本运算，每小题4分，满分16分．
（13）2 （14）
（15）1 （16）2n（n－1）
三、解答题
（17）本小题考查线面关系和棱锥体积计算，考查空间想象能力和逻辑推理能力，满分12分．
解：（Ⅰ）直角梯形ABCD的面积是：
∴四棱锥S－ABCD的体积是：
（Ⅱ）延长BA、CD相交于点E，连结SE，则SE是所求二面角的棱；
∵AD∥BC，BC＝2AD ∴EA＝AB＝SA，∴SE⊥S（B）
∵SA⊥面ABCD，得面SEB⊥面EBC，EB是交线，又BC⊥EB，
∴BC⊥平面SEB，故SB是SC在面SEB上的射影，
∴CS⊥SE，故∠BSC是所求二面角的平面角．
∵
，BC＝1，BC⊥SB
∴
即所求二面角的正切值为
．
（18）本小题考查复数的基本性质和基本运算，以及分析问题和解决问题的能力，满分12分．
解：（Ⅰ）
∴
， z1 ＝
．
（Ⅱ）设
，则
当
时，
取得最大值
，从而得到
的最大值为
．
|
|
（19）本小题考查抛物线的概念和性质，直线的方程和性质，运算能力和逻辑推理能力，满分12分．
证明：因为抛物线
（p＞0）的焦点为F（
，0），所以经过点F的直线AB的方程可设为：
4分
代入抛物线方程得：
若记A（x1，y1），B（x2，y2），则y1、y2是该方程的两根，所以
．
因为BC∥x轴，且点C在准线
上，∴点C的坐标为（
），故直线CO的斜率为
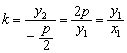，即k也是直线OA的斜率，所以直线AC经过原点O．
（20）本小题考查排列、组合、二项式定理、不等式的基本知识和逻辑推理能力，满分12分．
（Ⅰ）证明：对于1＜i≤m，有
同理
由于m＜n，对整数k＝1，2，…，i－1，有
∴
，即
．
（Ⅱ）由二项式定理有
，
由（Ⅰ）知，而
1＜i≤m＜n
∴
，因此
又
（m＜i≤n）
∴
，即．
（21）本小题主要考查建立函数关系式、数列求和、不等式等基础知识；考查综合运用数学知识解决实际问题的能力，满分12分．
解：（Ⅰ）第一年投入为800万元，第二年投入为800×
万元，…，第n年投入为800×
万元．
∴n年内的总投入为：
；
第一年旅游业收入为400，第二年旅游业收入为400×
万元，…，第n年旅游业收入为400×
万元
∴n年内旅游业总收入为：
（Ⅱ）设至少经过n年旅游业的总收入才能超过总投入，由此bn－an＞0
即
，化简得：
令
，代入上式得：5x2－7x＋2＞0，解得：x＜
或x＞1（舍去）
∴
，由此得n≥5．
答：至少经过5年旅游业的总收入才能超过总投入．
（22）本小题主要考查函数的概念、图象，函数的奇偶性和周期性以及数列极限等基础知识，考查运算能力和逻辑思维能力，满分14分．
（Ⅰ）解：由
知：
≥0，x∈[0，1]
∵
，f （1）＝a＞0，∴
∵
，∴
（Ⅱ）证明：依题设y＝f （x）关于直线x＝1对称，
故f （x）＝f （1＋1－x），即f （x）＝f （2－x），x∈R
又由f （x）是偶函数知f （－x）＝f （x），x∈R
将上式中－x以x代换，得f （x）＝f （x＋2），x∈R
这表明f （x）是R上的周期函数，且2是它的一个周期．
（Ⅲ）解：由（Ⅰ）知f （x）＞0，x∈[0，1]
∴
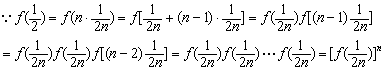
∵f （x）的一个周期是2，∴
，因此
∴
．