普通高考测试题数学(二)
本试卷分第一部分(选择题)和第二部分(非选择题)两部分.第一部分1至2页,第二部分3至4页,满分![]() 分,考试时间
分,考试时间![]() 分钟.
分钟.
第一部分(选择题,共50分)
注意事项:
1. 答第一部分前,考生务必将自己的姓名、考生号、考试科目用铅笔涂写在答题卡上.
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡
皮擦干净后,再选涂其它答案,不能答在试题卷上.
3. 考试结束,监考人员将本试卷和答题卡一并收回.
参考公式:
如果事件![]() 、
、![]() 互斥,那么 球的表面积公式
互斥,那么 球的表面积公式
![]() ,
, ![]()
如果事件![]() 、
、![]() 相互独立,那么 其中
相互独立,那么 其中![]() 表示球的半径
表示球的半径
![]() ,
,
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合![]() ,
,![]() ,则
,则![]() 的元素个数为
的元素个数为
A.0 个 B.1 个 C.2 个 D.无穷多个
2.![]()
A.![]() B.
B.![]() C.
C.![]() D.不存在
D.不存在
3.设复数:![]() 为实数,则b=
为实数,则b=
A.2 B.1 C.-1 D.-2
4.在平面直角坐标系中,函数![]() 的图象
的图象
A.关于![]() 轴对称 B.关于原点轴对称 C.关于
轴对称 B.关于原点轴对称 C.关于![]() 轴对称 D.关于直线
轴对称 D.关于直线![]() 轴对称
轴对称
5.在△ABC中,D分BC的比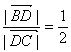 ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.设三棱锥的3个侧面两两互相垂直,且侧棱长均为![]() ,则其外接球的表面积为
,则其外接球的表面积为
A.![]() B.
B. ![]() C.
C.
![]() D.
D.![]()
7.已知集合A![]() ,那么
,那么![]() 为区间
为区间
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8.设a,b,c表示三条直线,![]() 表示两个平面,下列命题中不正确的是
表示两个平面,下列命题中不正确的是
A. ![]()
![]() B.
B.
C. 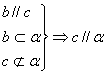 D.
D.
![]()
9. 设![]() 是双曲线
是双曲线![]() 上任一点,过P作双曲线两条渐近线的平行线分别交另一条渐近线于Q、R,O为坐标原点,则平行四边形OQPR的面积为
上任一点,过P作双曲线两条渐近线的平行线分别交另一条渐近线于Q、R,O为坐标原点,则平行四边形OQPR的面积为
A.![]() B.
B. ![]() C.
C.
![]() D.不能确定
D.不能确定
10.定义在R上的函数![]() ,满足
,满足![]() ,且
,且![]() ,那么在下面四个式子 ①
,那么在下面四个式子 ①![]() ②
②![]() ③
③![]() ④
④![]() 中与
中与![]() 相等的是
相等的是
A.①③ B. ①② C. ①②③④ D.①②③
第二部分(非选择题,共100分)
注意事项:
1. 第二部分共2页,用黑色钢笔或圆珠笔直接答在答题卷中.
2. 答卷前将密封线内的项目填写清楚.
二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷相应题目上.
11.已知函数![]() 和
和![]() 互为反函数,则
互为反函数,则![]() = ,
= ,![]() .
.
12.已知一盒子中有散落的围棋棋子10粒,其中7粒黑子,3粒白子,从中任意取出2粒,若![]() 表示取得白子的个数,则E
表示取得白子的个数,则E![]() 等于 .
等于 .
13.已知![]() 的展开式中第5项为含有
的展开式中第5项为含有![]() 的项,则展开式中倒数第二项的系数是
.
的项,则展开式中倒数第二项的系数是
.
14.在条件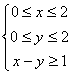 下,
下, ![]() 的取值范围是________ .
的取值范围是________ .
三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.
15.(本题满分12分)
已知函数![]() 恒过点
恒过点![]() .
.
(1)求![]() 的值;
的值;
(2)求函数![]() 的最小正周期及单调递减区间.
的最小正周期及单调递减区间.
16.(本题满分13分)
我省某校要进行一次月考,一般考生必须考5 门学科,其中语、数、英、综合这四科是必考科目,另外一门在物理、化学、政治、历史、生物、地理、英语Ⅱ中选择.为节省时间,决定每天上午考两门,下午考一门学科,三天半考完.
(1)若语、数、英、综合四门学科安排在上午第一场考试,则“考试日程安排表”有多少种不同的安排方法;
(2)如果各科考试顺序不受限制,求数学、化学在同一天考的概率是多少?
17.(本题满分13分)
一个计算装置有一个数据入口A和一输出运算结果的出口B,将自然数列![]()
![]() 中的各数依次输入A口,从B口得到输出的数列
中的各数依次输入A口,从B口得到输出的数列![]() ,结果表明:①从 A口输入
,结果表明:①从 A口输入![]() 时,从B口得
时,从B口得![]() ;②当
;②当![]() 时,从A口输入
时,从A口输入![]() ,从B口得的结果
,从B口得的结果![]() 是将前一结果
是将前一结果![]() 先乘以自然数列
先乘以自然数列![]() 中的第
中的第![]() 个奇数,再除以自然数列
个奇数,再除以自然数列![]() 中的第
中的第![]() 个奇数.试问:
个奇数.试问:
⑴从 A口输入2和3时,从B口分别得到什么数?
⑵从 A口输入100时,从B口得到什么数?说明理由.
18、(本题满分14分)
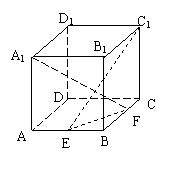 在棱长为2的正方体
在棱长为2的正方体![]() —
—![]() 中E、F 分别是棱AB、BC上
中E、F 分别是棱AB、BC上
的动点,且AE=BF.
(1)求证:![]() ;
;
(2)当AE为何值时,三棱锥![]() 的体积最大,
的体积最大,
求此时二面角![]() —EF—B的大小(结果用反三角函数表示).
—EF—B的大小(结果用反三角函数表示).
![]() 19、(本题满分14分)
19、(本题满分14分)
![]()
![]()
![]()
![]()
![]()
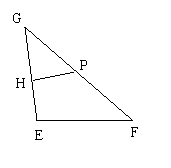
![]() 如图,已知E、F为平面上的两个定点
如图,已知E、F为平面上的两个定点![]() ,
,![]() ,且
,且![]() ,
,![]() ·
·![]() ,(G为动点,P是HP和GF的交点)
,(G为动点,P是HP和GF的交点)
(1)建立适当的平面直角坐标系求出点![]() 的轨迹方程;
的轨迹方程;
 (2)若点
(2)若点![]() 的轨迹上存在两个不同的点
的轨迹上存在两个不同的点![]() 、
、![]() ,且线段
,且线段![]() 的中垂线与
的中垂线与![]()
![]() (或
(或![]() 的延长线)相交于一点
的延长线)相交于一点![]() ,则
,则![]() <
<![]() (
(![]() 为
为![]() 的中点).
的中点).
20、(本小题满分14分)
设函数![]() 、
、![]() R).
R).
(1)若![]() ,过两点(0,0)、(
,过两点(0,0)、(![]() ,0)的中点作与
,0)的中点作与![]() 轴垂直的直线,与函数
轴垂直的直线,与函数![]() 的图象交于点
的图象交于点![]() ,求证:函数
,求证:函数![]() 在点P处的切线过点(
在点P处的切线过点(![]() ,0);
,0);
(2)若![]() ),且当
),且当![]() 时
时![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
普通高考测试题(二)
数学
答案及评分意见
一、选择题:本大题共10小题,每小题5分,共50分.
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 | C | A | D | B | C | B | A | D | C | D |
二、填空题:本大题共4小题,每小题5分,共20分.
11.1,3
12.![]() 13.
13.![]() 14.
14.![]()
三、解答题:
15、(本题满分12分)
解(1)依题意得
![]() -------------------2分
-------------------2分
解得![]() ---------------------------4分
---------------------------4分
(2)由![]()
![]() ----6分
----6分
∴函数![]() 的最小正周期
的最小正周期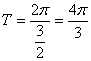 -------8分
-------8分
由![]() ,得
,得
![]()
![]() ---------10分
---------10分
∴函数![]() 的单调递减区间为
的单调递减区间为![]() ----12分
----12分
16、解:(1)语、数、英、综合四门学科安排在上午第一场考试共有:
![]() 种排法,
-------------1分
种排法,
-------------1分
其它七科共有![]() 种排法, -------------2分
种排法, -------------2分
由![]()
![]()
![]() =
=![]() ,得 -------------3分
,得 -------------3分
“考试日程安排表”有![]() 种不同的安排方法.-------------4分
种不同的安排方法.-------------4分
(2)数学、化学安排第四天上午考共有:![]() 种方法,---------6分
种方法,---------6分
安排前三天同一天考共有:![]() 种方法 ---------8分
种方法 ---------8分
∴所求的概率![]() -----12分
-----12分
17、(本题满分13分)
解:(1)由题意知
![]()
![]() -----------2分
-----------2分
![]() -------------3分
-------------3分
所以从 A口输入2和3时,从B口分别得到![]() 和
和![]() -------4分
-------4分
(2)猜想![]() ---------------6分
---------------6分
下面用数学归纳法证明
ⅰ)当![]() 时,猜想显然成立.
---------------7分
时,猜想显然成立.
---------------7分
ⅱ)假如![]() 时,猜想成立,
时,猜想成立,
即![]() ,
,
那么![]() 时,
时,![]()
![]() =
=![]()
=![]() ---------------10分
---------------10分
猜想成立,因此对一切正整数![]() ,猜想也成立
,猜想也成立
当![]() 时,即在从
A口输入2006时,从B口得到
时,即在从
A口输入2006时,从B口得到
![]() ---------------13分
---------------13分
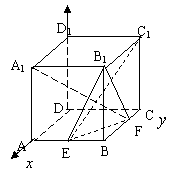 18、(本题满分14分)
18、(本题满分14分)
(1)证明:如图,以D为原点建立空间直角坐标系.-------1分
设 AE=BF=![]() ,则
,则![]() 、
、![]() 、
、
![]() 、
、![]() , ------------------3分
, ------------------3分
![]()
![]()
![]() ,
,![]()
![]()
![]() ∵
∵![]() ·
·![]()
![]() ,-----5分
,-----5分
∴![]() ⊥
⊥![]()
![]() ----------------6分
----------------6分
(2)解:记![]() ,
,![]() ,则
,则![]() ,-----8分
,-----8分
三棱锥![]() 的体积
的体积
![]()
当且仅当![]() 时,等号成立
时,等号成立
故当AE=1时,三棱锥![]() 的体积取得最大值-----10分
的体积取得最大值-----10分
此时,![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连
,连![]() ,可知
,可知![]() ,
,
∴![]() 是二面角
是二面角![]() 的平面角,------12分
的平面角,------12分
在直角三角形![]() 中,直角边
中,直角边![]() ,
,![]() 是斜边上的高,
是斜边上的高,
∴![]() ,
,![]() ,
,
故二面角![]() 的大小为
的大小为![]() 。---------14分
。---------14分
 19、(本题满分12分)
19、(本题满分12分)
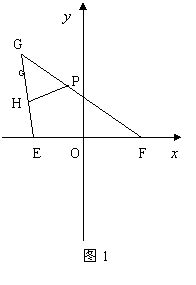
解:(1)如图1,以![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 的中垂线为
的中垂线为![]() 轴,
轴,
建立平面直角坐标系。----------------------------------------1分
![]()
![]()
![]()
![]() 由题设
由题设![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() ∴
∴![]() ,而
,而![]() -------------3分
-------------3分
∴点![]() 是以
是以![]() 、
、![]() 为焦点、长轴长为10的椭圆,
为焦点、长轴长为10的椭圆,
故点![]() 的轨迹方程是:
的轨迹方程是:![]() -----------------4分
-----------------4分
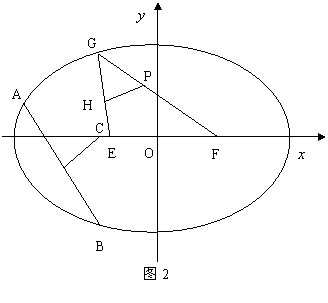
(2)如图2 ,设![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ∴
∴![]() ,且
,且![]() ,--------------------------------6分
,--------------------------------6分
即![]()
![]()
又![]() 、
、![]() 在轨迹上,
在轨迹上,
 ∴
∴![]() ,
,![]()
即![]() ,
,
![]() ---------------8分
---------------8分
代入整理得:
![]()
∵![]() ,∴
,∴![]() .---------------------10分
.---------------------10分
∵![]() ,
,![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]()
![]() ∴
∴![]() ,即
,即![]() <
<![]() .---------------14分
.---------------14分
20、(本题满分14分)
解:
(1)由已知![]() …………2分
…………2分
![]()
所求,所求切线斜率为![]() …………4分
…………4分
切线方程为![]()
所以,函数![]() 过点P的切线过点(
过点P的切线过点(![]() ,0) …………6分
,0) …………6分
(2)因为![]() ,所以
,所以![]() ,
,
![]()
当![]() 时,函数
时,函数![]() 上单调递增,在(
上单调递增,在(![]() ,
,![]() )单调递减,
)单调递减,
在![]() 上单调递增. …………8分
上单调递增. …………8分
![]() 所以,根据题意有
所以,根据题意有 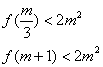 即
即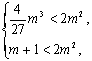
解之得![]() ,结合
,结合![]() ,所以
,所以![]() .…………10分
.…………10分
当![]() 时,函数
时,函数![]() 单调递增.
单调递增.
所以,根据题意有![]()
即![]() , 整理得
, 整理得![]() (
(![]() )
)
令![]() ,
,![]()
![]() ,所以“
,所以“![]() ”不等式无解. …13分
”不等式无解. …13分
综上可知:![]() .
…………14分
.
…………14分