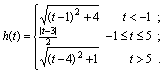普通高校春季高考数学试卷
一、填空题（本大题满分48分）
1．若复数
满足
，则的实部是__________.
2．方程
的解
__________.
3．在
中，
分别是
、
、
所对的边。若
，
，
，
则
__________.
4．过抛物线
的焦点
作垂直于
轴的直线，交抛物线于
、
两点，则以为圆心、
为直径的圆方程是________________.
5．已知函数
，则方程
的解__________.
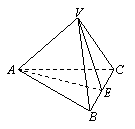
6．如图，在底面边长为2的正三棱锥
中，
是
的中点，若
的面积是
，则侧棱
与底面所成角的大小为_____________
(结果用反三角函数值表示).
7．在数列
中，
，且对任意大于1的正整数
，点
在直线
上，则
_____________.
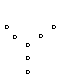
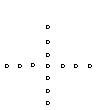8．根据下列5个图形及相应点的个数的变化规律，试猜测第个图中有___________个点.
 | |||||
 | |||||
| |||||
（1） （2） （3） （4） （5）
9．一次二期课改经验交流会打算交流试点学校的论文5篇和非试点学校的论文3篇。若任意排列交流次序，则最先和最后交流的论文都为试点学校的概率是__________（结果用分数表示）.
10．若平移椭圆
，使平移后的椭圆中心在第一象限，且它与轴、
轴分别
只有一个交点，则平移后的椭圆方程是___________________.
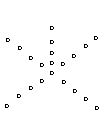
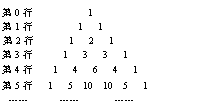11．如图，在由二项式系数所构成的杨辉三角形中，第
_____行中从左至右第14与第15个数的比为
.
12．在等差数列中，当
时，
必定是常数数列。然而在等比数列中，对某
些正整数
、
，当时，非常数数
列的一个例子是____________.
二、填空题（本大题满分16分）
13．下列函数中，周期为1的奇函数是 （ ）
（A）
（B）
（C）
（D）
14．若非空集合
，则“
或
”是“
”的
（ ）
（A）充分非必要条件 （B）必要非充分条件 （C）充要条件 （D）既非充分又非必要条件
15．在中，有命题
①
；②
；③若
，则为等
腰三角形；④若
，则为锐角三角形.
上述命题正确的是 （ ）
（A）①② （B）①④ （C）②③ （D）②③④
16．若
，
，则下列不等式恒成立的是 （ ）
（A）
（B）
（C）
（D）
三、解答题（本大题满分86分）
17. （本题满分12分） 在直角坐标系
中，已知点
和点
，其中
. 若向量
与
垂直，求的值.
18. （本题满分12分）已知实数
满足不等式
，试判断方程
有无实根，并给出证明.
19. (本题满分14分) 本题共有2个小题，第一小题满分6分，第2小题满分8分.
某市2003年共有1万辆燃油型公交车。有关部门计划于2004年投入128辆电力型公交车，
随后电力型公交车每年的投入比上一年增加50%，试问：
(1) 该市在2010年应该投入多少辆电力型公交车？
(2) 到哪一年底，电力型公交车的数量开始超过该市公交车总量的
？
20. (本题满分14分) 本题共有2个小题，第一小题满分6分，第2小题满分8分.
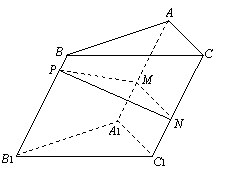
如图，点
为斜三棱柱
的侧棱
上一点，
交
于点
，
交
于点
.
(1) 求证：
；
(2) 在任意
中有余弦定理：
. 拓展到空间，
类比三角形的余弦定理，写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角
之间的关系式，并予以证明.
 |
21.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分，第3小题满分6分.
已知函数
，
（
为正常数），且函数
与
的图象在轴上的截距相等。
（1）求的值；
（2）求函数
的单调递增区间；
（3）若为正整数，证明：
.
22.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分，第3小题满分8分.
已知倾斜角为
的直线
过点
和点，在第一象限，
.
(1) 求点的坐标；
(2) 若直线与双曲线
相交于、两点，且线段
的中点坐标为
，求的值；
(3) 对于平面上任一点，当点
在线段上运动时，称
的最小值为与线段的距离. 已知点在轴上运动，写出点
到线段的距离
关于
的函数关系式.
普通高校春季高考数学试卷参考答案
一、填空题
1．1
2．2 3．2
4．
5．1
6．
7．3
8．
9．
10．
11．34
12．
，
与
同为奇数或偶数
二、选择题 13．D 14．B 15．C 16．B
三、解答题
17. 由
，得
，利用
，化简后得
，于是
或
，
，
.
18. 由
，解得
，
. 方程
的判别式
.
，
，
，由此得方程无实根.
19.(1)该市逐年投入的电力型公交车的数量组成等比数列
，其中
则在2010年应该投入的电力型公交车为
（辆）。
(2)记
，依据题意，得
。于是
（辆），即
，
则有
因此
。所以，到2011年底，电力型公交车的数量开始超过该市公交车总量的
。
20. (1) 证：
；
(2) 解：在斜三棱柱
中，有
，其中
为
平面
与平面
所组成的二面角.
上述的二面角为
,在
中，
，
由于
，
有.
21.(1)由题意，
，
又
，所以
。
(2)
当
时，
，它在
上单调递增；
当
时，
，它在
上单调递增。
(3)设
，考查数列
的变化规律：
解不等式
，由
，上式化为
解得
，因
得
，于是
，而
所以
。
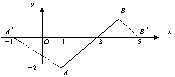
22. (1) 直线
方程为
，设点
，由
及
，
得
，
，点
的坐标为
。
（2）由
得
，设
，则
，得
。
（3）(解法一)设线段上任意一点
坐标为
，
，
记
，
当
时，即
时，
，
当
，即
时，
在
上单调递减，∴
；
当
，即
时，在上单调递增，
。
综上所述，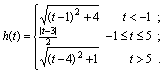
(解法二) 过
、两点分别作线段的垂线，交
轴于
、
，
当点
在线段
上，即
时，由点到直线的距离公式得：
；
当点的点在点
的左边，时，
；
当点的点在点的右边，
时，
。
综上所述，