全国普通高考高等学校招生统一考试数学卷(新课程卷)
数 学(理工农医类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页.第Ⅱ卷3至10页.共150分.考试时间120分钟.
第Ⅰ卷(选择题共60分)
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一项是符合题目要求的.
(1)设集合A和B都是坐标平面上的点集![]() ,映射
,映射![]() 把集合A中的元素
把集合A中的元素![]() 映射成集合B中的元素
映射成集合B中的元素![]() ,则在映射
,则在映射![]() 下,象
下,象![]() 的原象是
的原象是
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
(2)在复平面内,把复数![]() 对应的向量按顺时针方向旋转
对应的向量按顺时针方向旋转![]() ,所得向量对应的复数是
,所得向量对应的复数是
(A) 2![]() (B)
(B)
![]() (C)
(C)
![]() (D)
3
(D)
3![]()
(3)一个长方体共一顶点的三个面的面积分别是![]() ,
,![]() ,
,![]() ,这个长方体对角线的长是
,这个长方体对角线的长是
(A) 2![]() (B) 3
(B) 3![]() (C)
(C)
![]() (D)
6
(D)
6
(4)设![]() 、
、![]() 、
、![]() 是任意的非零平面向量,且相互不共线,则
是任意的非零平面向量,且相互不共线,则
①![]() ②
②![]()
③![]() 不与
不与![]() 垂直
④
垂直
④![]()
中,是真命题的有
(A) ①② (B) ②③ (C) ③④ (D) ②④
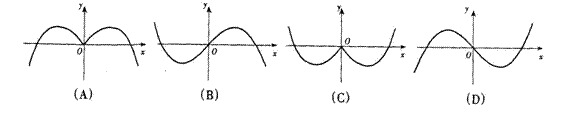
(5)函数![]() 的部分图象是
的部分图象是
|
|
(6)《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过800元的部分不必纳税,超过800元的部分为全月应纳税所得额.此项税款按下表分段累进计算:
全月应纳税所得额 税率
不超过500元的部分 5%
超过500元至2000元的部分 10%
超过2000元至5000元的部分 15%
… …
某人一月份应交纳此项税款26.78元,则他的当月工资、薪金所得介于
(A) 800~900元 (B) 900~1200元
(C) 1200~1500元 (D) 1500~2800元
(7)若![]() ,P=
,P=![]() ,Q=
,Q=![]() ,R=
,R=![]() ,则
,则
(A) R![]() P
P![]() Q (B)
P
Q (B)
P![]() Q
Q ![]() R
R
(C) Q ![]() P
P![]() R (D)
P
R (D)
P ![]() R
R![]() Q
Q
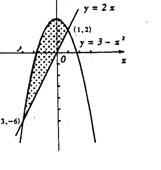 (8)右图中阴影部分的面积是
(8)右图中阴影部分的面积是
(A)
![]()
(B)
![]()
(C)
![]()
(D)
![]()
(9)一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
(10)过原点的直线与圆![]() 相切,若切点在第三象限,则该直线的方程是
相切,若切点在第三象限,则该直线的方程是
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
(11)过抛物线![]() 的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是
的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别是![]() 、
、![]() ,则
,则![]() 等于
等于
(A)
![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
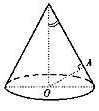 (12)如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分,则母线与轴的夹角的余弦值为
(12)如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分,则母线与轴的夹角的余弦值为
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D)
![]()
第Ⅱ卷(非选择题共90分)
二.填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
(13)某厂生产电子元件,其产品的次品率为5%,现从一批产品中任意地连续取出2件,其中次品数![]() 的概率分布是
的概率分布是
![]() 0 1 2
0 1 2
![]()
(14)椭圆![]() 的焦点为
的焦点为![]() 、
、![]() ,点P为其上的动点,当
,点P为其上的动点,当![]() 为钝角时,点P 横坐标的取值范围是________.
为钝角时,点P 横坐标的取值范围是________.
(15)设![]() 是首项为1的正项数列,且
是首项为1的正项数列,且![]() (
(![]() =1,2,3,…),则它的通项公式是
=1,2,3,…),则它的通项公式是![]() =________.
=________.
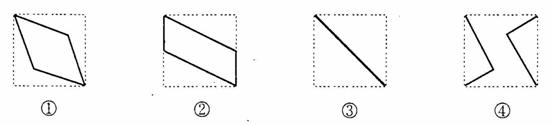
(16)如图,E、F分别为正方体的面![]() 、面
、面![]() 的中心,则四边形
的中心,则四边形![]() 在该正方体的面上的射影可能是_______.(要求:把可能的图的序号都填上)
在该正方体的面上的射影可能是_______.(要求:把可能的图的序号都填上)
 |
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
(17)(本小题满分10分)
甲、乙二人参加普法知识竞答,共有10个不同的题目,其中选择题6个,判断题4个.甲、乙二人依次各抽一题.
(I)甲抽到选择题、乙抽到判断题的概率是多少?
(II)甲、乙二人中至少有一人抽到选择题的概率是多少?
注意:考生在(18甲)、(18乙)两题中选一题作答,如果两题都答,只以(18甲)计分.
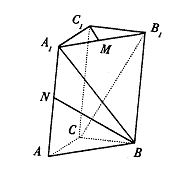 (18甲)(本小题满分12分)
(18甲)(本小题满分12分)
如图,直三棱柱ABC-![]() ,底面ΔABC中,CA=CB=1,∠BCA=
,底面ΔABC中,CA=CB=1,∠BCA=![]() ,棱
,棱![]() =2,M、N分别是
=2,M、N分别是![]() 、
、![]() 的中点.
的中点.
(I)求![]() 的长;
的长;
(II)求![]() ,
,![]()
![]() 的值;
的值;
(III)求证![]() .
.
(18乙)(本小题满分12分)
|
|
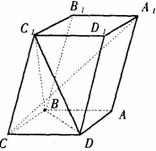
如图,已知平行六面体ABCD-![]() 的底面ABCD是菱形,且
的底面ABCD是菱形,且![]() =
=![]() =
=![]() =
=![]() .
.
(I)证明:![]() ⊥BD;
⊥BD;
(II)假定CD=2,![]() =
=![]() ,记面
,记面![]() 为
为![]() ,面CBD为
,面CBD为![]() ,求二面角
,求二面角 ![]() 的平面角的余弦值;
的平面角的余弦值;
(III)当![]() 的值为多少时,能使
的值为多少时,能使![]() 平面
平面![]() ?请给出证明.
?请给出证明.
(19)(本小题满分12分)
设函数![]() ,其中
,其中![]() .
.
(I)解不等式![]() ;
;
(II)求![]() 的取值范围,使函数
的取值范围,使函数![]() 在区间
在区间![]() 上是单调函数.
上是单调函数.
(20)(本小题满分12分)
用总长14.8m的钢条制成一个长方体容器的框架,如果所制做容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积.
(21)(本小题满分14分)
(I)已知数列![]() ,其中
,其中![]() ,且数列
,且数列![]() 为等比数列,求常数
为等比数列,求常数![]() .
.
(II)设![]() 、
、![]() 是公比不相等的两个等比数列,
是公比不相等的两个等比数列,![]() ,证明数列
,证明数列![]() 不是等比数列.
不是等比数列.
 (22)(本小题满分14分)
(22)(本小题满分14分)
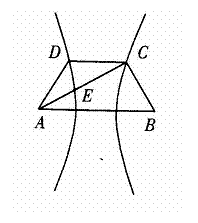
如图,已知梯形ABCD中![]() ,点E满足
,点E满足![]() =
=![]() ,双曲线过C、D、E三点,且以A、B为焦点.当
,双曲线过C、D、E三点,且以A、B为焦点.当![]() 时,求双曲线离心率
时,求双曲线离心率![]() 的取值范围.
的取值范围.
全国普通高等学校招生统一考试江西、天津卷
数学试题(理工农医类)参考答案
一、选择题:本题考查基本知识和基本运算.每小题5分,满分60分.
(1)B (2)B (3)C (4)D (5)D (6)C
(7)B (8)C (9)A (10)C (11)C (12) D
二、填空题:本题考查基本知识和基本运算.每小题4分,满分16分.
(13)![]() 0 1 2
0 1 2
![]() 0.9025 0.095 0.0025
0.9025 0.095 0.0025
(14)![]() (15)
(15)![]() (16)②③
(16)②③
三、解答题
(17)本小题主要考查等可能事件的概率计算及分析和解决实际问题的能力.满分10分.
解:(I)甲从选择题中抽到一题的可能结果有![]() 个,乙依次从判断题中抽到一题的可能结果有
个,乙依次从判断题中抽到一题的可能结果有![]() 个,故甲抽到选择题、乙依次抽到判断题的可能结果有
个,故甲抽到选择题、乙依次抽到判断题的可能结果有![]()
![]() 个;又甲、乙依次抽一题的可能结果有
个;又甲、乙依次抽一题的可能结果有![]()
![]() 个,所以甲抽到选择题、乙依次抽到判断题的概率为
个,所以甲抽到选择题、乙依次抽到判断题的概率为![]() ,所求概率为
,所求概率为![]() ; ——5分
; ——5分
(II)甲、乙二人依次都抽到判断题的概率为![]() ,故甲、乙二人中至少有一人抽到选择题的概率为
,故甲、乙二人中至少有一人抽到选择题的概率为![]() ,所求概率为
,所求概率为![]() .
.
或![]()
![]()
![]()
![]() ,所求概率为
,所求概率为![]() . ——10分
. ——10分
注意:考生在(18甲)、(18乙)两题中选一题作答,如果两题都答,只以(18甲)计分.
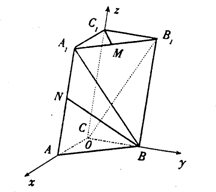
(18甲)本小题主要考查空间向量及运算的基本知识.满分12分.
如图,以C为原点建立空间直角坐标系O![]() .
.
 |
(I)解:依题意得B
∴![]() ——2分
——2分
(II)解:依题意得![]()
![]() ,B
,B![]() ,C
,C![]() ,
,![]()
![]() .
.
∴![]() ,
,![]() .
.
![]()
![]() ,
,![]() ,
,![]() . ——5分
. ——5分
∴![]()
![]()
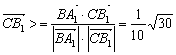 ——9分
——9分
(III)证明:依题意得![]()
![]() ,M
,M![]()
![]()
![]() ,
,![]()
![]() ,
,
∴ ![]()
![]()
![]() ,∴
,∴![]()
![]() , ∴A1B⊥C1M. ——12分
, ∴A1B⊥C1M. ——12分
(18乙)本小题主要考查直线与直线、直线与平面的关系,逻辑推理能力.满分12分.
(I)证明:连结![]() 、AC,AC和BD交于O,连结
、AC,AC和BD交于O,连结![]() .
.
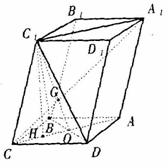 ∵ 四边形ABCD是菱形,
∵ 四边形ABCD是菱形,
∴ AC⊥BD,BC=CD.
又∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∵ DO=OB,
∴ ![]() BD, ——2分
BD, ——2分
但 AC⊥BD,AC∩![]() =O,
=O,
∴ BD⊥平面![]() .
.
又 ![]() 平面
平面![]() ,
,
∴ ![]() BD.
——4分
BD.
——4分
(II)解:由(I)知AC⊥BD,![]() BD,
BD,
∴ ![]() 是二面角
是二面角![]() 的平面角.
的平面角.
在![]() 中,BC=2,
中,BC=2,![]() ,
,![]() ,
,
∴ ![]() .
——6分
.
——6分
∵ ∠OCB=![]() ,
,
∴ OB=![]() BC=1.
BC=1.
∴ ![]() ,
,
∴ ![]() 即
即![]() .
.
作![]() ⊥OC,垂足为H.
⊥OC,垂足为H.
∴ 点H是OC的中点,且OH![]() ,
,
所以 ![]() .
——8分
.
——8分
(III)当![]() 时,能使
时,能使![]() ⊥平面
⊥平面![]() .
.
证法一:
∵ ![]() ,
,
∴ BC=CD=![]() ,
,
又 ![]() ,
,
由此可推得BD=![]() .
.
∴三棱锥C- ![]() 是正三棱锥 ——10分
是正三棱锥 ——10分
设![]() 与
与![]() 相交于G.
相交于G.
∵![]() ∥AC,且
∥AC,且![]() ∶OC=2∶1,
∶OC=2∶1,
∴![]() ∶GO=2∶1.
∶GO=2∶1.
又![]() 是正三角形
是正三角形![]() 的BD边上的高和中线,
的BD边上的高和中线,
∴点G是正三角形![]() 的中心,
的中心,
∴CG⊥平面![]() .
.
即![]() ⊥平面
⊥平面![]() ——12分
——12分
证法二:
由(I)知,BD⊥平面![]() ,
,
∵![]()
![]() 平面
平面![]() ,∴BD⊥
,∴BD⊥![]() . ——10分
. ——10分
当![]() 时 ,平行六面体的六个面是全等的菱形,
时 ,平行六面体的六个面是全等的菱形,
同BD⊥![]() 的证法可得
的证法可得![]() ⊥
⊥![]() .
.
又 BD∩![]() =B,
=B,
∴![]() ⊥平面
⊥平面![]() . ——12分 (19)本小题主要考查不等式的解法、函数的单调性等基本知识、分类讨论的数学思想方法和运算、推理能力.满分12分.
. ——12分 (19)本小题主要考查不等式的解法、函数的单调性等基本知识、分类讨论的数学思想方法和运算、推理能力.满分12分.
思路1:(I)不等式![]() 即
即
![]() ,
,
由此得![]() ,即
,即![]() ,其中常数
,其中常数![]() .
.
所以,原不等式等价于
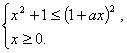
即![]() ——3分
——3分
所以,当![]() 时,所给不等式的解集为
时,所给不等式的解集为![]() ;
;
当![]() 时,所给不等式的解集为
时,所给不等式的解集为![]() . ——6分(II)在区间
. ——6分(II)在区间![]() 上任取
上任取![]() ,
,![]() ,使得
,使得![]() <
<![]() .
.
![]()
![]()
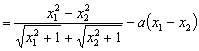
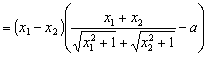 . ——8分
. ——8分
(i) 当![]() 时,
时,
∵![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
即![]() .
.
所以,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是单调递减函数.
——10分
上是单调递减函数.
——10分
(ii)当![]() 时,在区间
时,在区间![]() 上存在两点
上存在两点![]() ,
,![]() ,满足
,满足
![]() ,
,![]() ,即
,即![]()
![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上不是单调函数.
上不是单调函数.
综上,当且仅当![]() 时,函数
时,函数![]() 为区间
为区间![]() 上的单调函数. ——12分
上的单调函数. ——12分
思路2:![]() ——4分
——4分
(i)当![]() 时,有
时,有
![]() ,
,
此时![]() .函数
.函数![]() 在区间(—∞,+∞)上是单调递减函数.
在区间(—∞,+∞)上是单调递减函数.
但f(0)=1,因此,当且仅当x≥0时
f(x)≤1 ——8分
(ii)当0<a<1时:
解不等式![]() 得
得![]() ,f(x)在区间
,f(x)在区间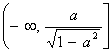 上是单调递减函数;
上是单调递减函数;
同理,解不等式![]() 得
得![]() ,f(x)在区间
,f(x)在区间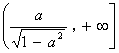 上是单调递增函数.
上是单调递增函数.
解方程f(x)=1得
![]() .
.
因为![]() ,
,
所以,当且仅当![]() .
.
综上:(Ⅰ)当a≥1时,![]() 的解集为
的解集为![]() ;
;
当0<a<1时 ![]() 的解集为
的解集为![]() .
.
(Ⅱ)当且仅当a≥1时,f(x)在区间[0,+∞]上是单调函数. ——12分
(20)本小题主要考查应用所学导数的知识、思想和方法解决实际问题的能力,建立函数式、解方程、不等式、最大值等基础知识.满分12分.
解:设容器底面短边长为![]() m,则另一边长为
m,则另一边长为![]() m,高为
m,高为
![]() .
.
由![]() 和
和![]() ,得
,得![]() ,
,
设容器的容积为![]() ,则有
,则有
![]()
![]() .
.
整理,得
![]() , ——4分
, ——4分
∴![]() . ——6分
. ——6分
令![]() ,有
,有
![]() ,
,
即![]() ,
,
解得![]() ,
,![]() (不合题意,舍去). ——8分
(不合题意,舍去). ——8分
从而,在定义域(0,1.6)内只有在![]() 处使
处使![]() .由题意,若
.由题意,若![]() 过小(接近0)或过大(接近1.6)时,
过小(接近0)或过大(接近1.6)时,![]() 值很小(接近0),因此,当
值很小(接近0),因此,当![]() 时
时![]() 取得最大值
取得最大值
![]() ,
,
这时,高为![]() .
.
答:容器的高为1.2m时容积最大,最大容积为![]() . ——12分(21)本小题主要考查等比数列的概念和基本性质,推理和运算能力.满分14分.
. ——12分(21)本小题主要考查等比数列的概念和基本性质,推理和运算能力.满分14分.
解:(I)因为![]() 是等比数列,故有
是等比数列,故有
![]() ,
,
将![]() 代入上式,得
代入上式,得
![]()
=![]() ——4分
——4分
即![]()
=![]() ,
,
整理得![]() ,
,
解得![]() =2或
=2或![]() =3. ——8分
=3. ——8分
(II)设![]() 、
、![]() 的公比分别为
的公比分别为![]() 、
、![]() ,
,![]() ≠
≠![]() ,
,![]() .
.
为证![]() 不是等比数列只需证
不是等比数列只需证![]() .
.
事实上,![]() ,
,
![]()
![]() . ——12分
. ——12分
由于![]() ,
,![]() ,又
,又![]() 、
、![]() 不为零,
不为零,
因此,![]() ,故
,故![]() 不是等比数列. ——14分
不是等比数列. ——14分
(22)本小题主要考查坐标法、定比分点坐标公式、双曲线的概念和性质,推理、运算能力和综合应用数学知识解决问题的能力.满分14分.
解:如图,以AB的垂直平分线为![]() 轴,直线AB为
轴,直线AB为![]() 轴,建立直角坐标系
轴,建立直角坐标系![]() ,则CD⊥
,则CD⊥![]() 轴.因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于
轴.因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于![]() 轴对称.
轴对称.
——2分
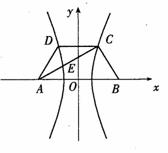 依题意,记A
依题意,记A![]() ,C
,C![]() ,E
,E![]() ,其中
,其中![]() 为双曲线的半焦距,
为双曲线的半焦距,![]() 是梯形的高.
是梯形的高.
由![]() ,即
,即![]() 得
得
![]() . ——5分
. ——5分
设双曲线的方程为![]() ,则离心率
,则离心率![]() .
.
由点C、E在双曲线上,将点C、E的坐标和![]() 代入双曲线的方程得
代入双曲线的方程得
|
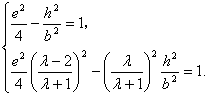
由①式得![]() , ③
, ③
将③式代入②式,整理得
![]() ,
,
故 ![]() .
——10分
.
——10分
由题设![]() 得,
得,![]() .
.
解得
![]() .
.
所以,双曲线的离心率的取值范围为![]() .
——14分
.
——14分