普通高等学校春季招生考试数学试题
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷1至2页．第Ⅱ卷3至8页．共150分．考试时间120分钟．
第Ⅰ卷（选择题 共60分）
注意事项：
1.答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上．
2.每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用像皮擦干净后，再选涂其它答案，不能答在试题卷上．
3.考试结束，监考人将本试卷和答题卡一并收回．
参考公式： 正棱台、圆台的侧面积公式
三角函数的积化和差公式
其中
、
分别表示上、下底面周长，
表示斜高或母线长
球体的体积公式 
其中
表示球的半径
一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
（1）集体
的子集个数是
（A）32 （B）31 （C）16 （D）15
（2）函数
对于任意的实数
都有
（A）
（B）
（C）
（D）
（3）
（A）0 （B）2 （C）
（D）
（4）函数
的反函数是
（A）
（B）
（C）
（D）
（5）已知
、
是椭圆
的两焦点，过点的直线交椭圆于点A、B，若
，则
（A）11 （B）10 （C）9 （D）16
（6）设动点P在直线
上，O为坐标原点．以OP为直角边、点O为直角顶点作等腰
，则动点Q的轨迹是
（A）圆 （B）两条平行直线 （C）抛物线 （D）双曲线
（7）已知
，那么
等于
（A）
（B）8 （C）18 （D）
（8）若A、B是锐角
的两个内角，则点
在
（A）第一象限 （B）第二象限 （C）第三象限 （D）第四象限
（9）如果圆锥的侧面展开图是半圆，那么这个圆锥的顶角（圆锥轴截面中两条母线的夹角）是
（A）
（B）
（C）
（D）
（10）若
为实数，且
，则
的最小值是
|
（D）
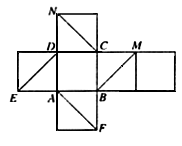
（11）右图是正方体的平面展开图．在这个正方体中，
①
平行
②CN与BE是异面直线
③CN与BM成角
④DM与BN垂直
以上四个命题中，正确命题的序号是
（A）①②③ （B）②④
（C）③④ （D）②③④
（12）根据市场调查结果，预测某种家用商品从年初开始的
个月内累积的需求量
（万件）近似地满足
按此预测，在本年度内，需求量超过1.5万件的月份是
（A）5月、6月 （B）6月、7月 （C）7月、8月 （D）8月、9月
第Ⅱ卷（非选择题共90分）
注意事项：
1.第Ⅱ卷共6页，用钢笔或圆珠笔直接答在试题卷中．
2.答卷前将密封线内的项目填写清楚．
二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．
（13）已知球内接正方体的表面积为S，那么球体积等于_______________．
（14）椭圆
长轴上一个顶点为A，以A为直角顶点作一个内接于椭圆的等腰直角三角形，该三角形的面积是_______________．
（15）已知
、
、
均为锐角），那么
的最大值等于____________________．
（16）已知
、是直线，
、、是平面，给出下列命题：
① 若
，则
；
②若
∥，
，则∥；
③若不垂直于，则不可能垂直于内的无数条直线；
④若
，∥，且
，则∥
∥．
其中正确的命题的序号是_______________（注：把你认为正确的命题的序号都填上）
三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．
（17）方程
有实根，且2、、为等差数列的前三项．求该等差数列公差
的取值范围．
（18）设函数
，求
的单调区间，并证明在其单调区间上的单调性．
（19）已知
．
（Ⅰ）证明
；
（Ⅱ）设
的辐角为，求
的值．
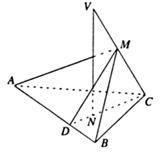
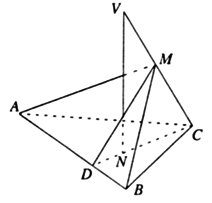
（20）已知VC是所在平面的一条斜线，点N是V在平面ABC上的射影，且N位于的高CD上．
之间的距离为
．
（Ⅰ）证明∠MDC是二面角M–AB–C的平面角；
（Ⅱ）当∠MDC=∠CVN时，证明VC
；
|
，求四面体MABC的体积．
（21）某摩托车生产企业，上年度生产摩托车的投入成本为1万元/辆，出厂价为1.2万元/辆，年销售量为1000辆．本年度为适应市场需求，计划提高产品档次，适度增加投入成本．若每辆车投入成本增加的比例为
，则出厂价相应提高的比例为0.75
，同时预计年销售量增加的比例为0.6．已知年利润=（出厂价–投入成本）
年销售量．
（Ⅰ）写出本年度预计的年利润
与投入成本增加的比例的关系式；
（Ⅱ）为使本年度的年利润比上年有所增加，问投入成本增加的比例应在什么范围内？
（22）已知抛物线
．过动点M（
，0）且斜率为1的直线与该抛物线交于不同的两点A、B．
（Ⅰ）若
的取值范围；
（Ⅱ）若线段AB的垂直平分线交AB于点Q，交轴于点N，试求
的面积．
普通高等学校春季招生考试
数学试题参考解答及评分标准
说明：
一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．
二、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．
三、解答右端所注分数，表示考生正确做到这一步应得的累加分数．
四、只给整数分数．选择题和填空题不给中间分．
一、选择题：本题考查基本知识和基本运算．每小题5分，满分60分．
（1）A （2）C （3）D （4）C （5）A （6）B
（7）D （8）B （9）C （10）B （11）C （12）C
二、填空题：本题考查基本知识和基本运算．每小题4分，满分16分．
（13）
（14）
（15）
（16）②④
三、解答题
（17）本小题主要考查等差数列，一元二次方程与不等式的基本知识．考查综合运用数学基础知识的能力．满分12分．
解：依题意，有
， ……2分
由方程有实根，得
，
即 
， ……6分
整理，得
， ……8分
解得 
，
∴ 
． ……12分
（18）本小题主要考查函数的基本性质，考查推理能力．满分12分．
解：函数
的定义域为
．
内是减函数
内也是减函数． ……4分
证明内是减函数．
取
，且
，那么
， ……6分
∵ 
，
∴ 
，
即内是减函数． ……9分
同理可证内是减函数． ……12分
（19）本小题考查复数的基本概念和运算．满分12分．
解：（Ⅰ）由 
，
得
． ……4分
因为 
，
所以 ． ……6分
（Ⅱ）因为
，
所以 
，而
，所以
，
，同理
，
．
由（Ⅰ）知 
，
即 
，
所以
的实部为
， ……8分
而的辐角为时，复数的实部为
，
所以 
……12分
（20）本小题考查运用直线与直线、直线与平面的基本性质证明线面关系的能力．满分12分．
（Ⅰ）证明：由已知，
，
∴
．
∴
． ……2分
又V、M、N、D都在VNC所在平面内，
所以，DM与VN必相交，且
，
∴∠MDC为二面角
的平面角． ……4分
（Ⅱ）证明：由已知，∠MDC=∠CVN，
在
中，
∠NCV=∠MCD，
又∵∠VNC=，
∴∠DMC=∠VNC=．
故有
， ……6分
∴
． ……8分
（Ⅲ）解：由（Ⅰ）、（Ⅱ），
，
∴
．
又∵∠
．
在
中，
． ……10分
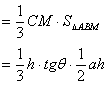
． ……12分
（21）本小题主要考查建立函数关系、运用不等式的性质和解法等数学知识解决实际问题的能力．满分12分．
解：（Ⅰ）由题意得
，
……4分
整理得
． ……6分
（Ⅱ）要保证本年度的利润比上年度有所增加，必须
即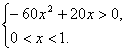 
……9分
解不等式得
．
答：为保证本年度的年利润比上年度有所增加，投入成本增加的比例应满足
． ……12分
（22）本小题考查直线与抛物线的基本概念及位置关系，考查运用解析几何的方法解决数学问题的能力．满分14分．
解：（Ⅰ）直线的方程为：
，
将 
，
得 
． ……2分
设直线与抛物线两个不同交点的坐标为
、
，
则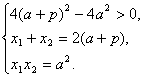 
……4分
又
，
∴ 
． ……6分
∵ 
，
∴ 
．
解得 
． ……8分
（Ⅱ）设
，由中点坐标公式，得
，
． ……10分
∴ 
．
又 
为等腰直角三角形，
∴ 
． ……14分