普通高等学校数学招生全国统一考试5

普通高等学校数学招生全国统一考试5数学

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷1至2页．第Ⅱ卷3至9页．共150分．考试时间120分钟．

第Ⅰ卷（选择题共60分）

注意事项：

1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上．

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．

3．考试结束，监考人将本试卷和答题卡一并收回．

正棱台、圆台的侧面积公式 其中c′、c分别表示上、下底面周长，l表示斜高或母线长 球体的体积公式 其中R表示球的半径

参考公式：

三角函数的积化和差公式

一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

（1）满足条件的集合M的个数是

（A）1　　　　　　　　 （B）2　　　　　　　　 （C）3　　　　　　　　 （D）4

（2）在平面直角坐标系中，已知两点A（cos80°，sin80°），B（cos20°，sin20°），则AB的值是

（A）　　　　　　　 （B）　　　　　　 （C）　　　　　　 （D）1

（3）下列四个函数中，以p为最小正周期，且在区间（，p）上为减函数的是

（A）y=cos²x　　　　　　　　　　　　　　　　　　　　　 （B）y=2sinx

（C）　　　　　　　　　　　　　　 　　　 （D）y=－cot x

（4）64个直径都为的球，记它们的体积之和为V_甲，表面积之和为S_甲；一个直径为a的球，记其体积为V_乙，表面积为S_乙，则

（A）V_甲>V_乙且S_甲>S_乙　　　　　　　　　　　　　　（B）V_甲<V_乙且S_甲<S_乙

（C）V_甲=V_乙且S_甲>S_乙　　　　　　　　　　　　　　（D）V_甲=V_乙且S_甲=S_乙

（5）已知某曲线的参数方程是（j为参数）．若以原点为极点，x轴的正半轴为极轴，长度单位不变，建立极坐标系，则该曲线的极坐标方程是

（A）r =1　　　　　　（B）rcos2q =1　　（C）r²sin2q =1　 （D）r²cos2q =1　

（6）给定四条曲线：①②③④其中与直线仅有一个交点的曲线是

（A）①②③　　　　（B）②③④　　　　 （C）①②④　　　　（D）①③④

（7）已知z₁，z₂∈C且 z₁=1．若z₁＋z₂=2i，则 z₁－z₂的最大值是

（A）6　　　　　　　　 （B）5　　　　　　　　 （C）4　　　　　　　　 （D）3

（8）若，则的值为

（A）3　　　　　　　　 （B）－3　　　　　　　（C）－2　　　　　　 （D）－

（9）12名同学分别到三个不同的路口进行车流量的调查，若每个路口4人，则不同的分配方案共有

（A）种 　　　　　　　　　　　　　　　　　 （B）3种

（C）种　　　　　　　　　　　　　　　　　　 （D）种　　　

（10）设命题甲：“直四棱柱ABCD－A₁B₁C₁D₁中，平面ACB₁与对角面BB₁D₁D垂直”；命题乙：“直四棱柱ABCD－A₁B₁C₁D₁是正方体”．那么，甲是乙的

（A）充分必要条件　　　　　　　　　　　　　　　　 （B）充分非必要条件

（C）必要非充分条件　　　　　　　　　　　　　　 （D）既非充分又非必要条件

（11）已知f（x）是定义在（－3，3）上的奇函数，当0<x<3时，f（x）的图象如图所示，那么不等式f（x）cosx<0的解集是

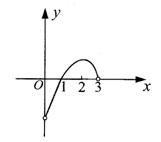（A）

（B）

（C）

（D）

（12）如图所示，fi（x）（i=1，2，3，4）是定义在［0，1］上的四个函数，其中满足性质：“对［0，1］中任意的x₁和x₂，任意l∈［0，1］，恒成立”的只有

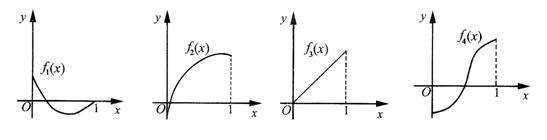
（A）f₁（x），f₃（x）　　　　　　　　　　　　　　　（B）f₂（x）

（C）f₂（x），f₃（x）　　　　　　　　　　　　　　　（D）f₄（x）

第Ⅱ卷（非选择题共90分）

注意事项：

1．第Ⅱ卷共7页，用钢笔或圆珠笔直接答在试题卷中．

2．答卷前将密封线内的项目填写清楚．

二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．

（13），，从小到大的顺序是_____________________．

（14）等差数列｛a_n｝中，a₁=2，公差不为零，且a₁，a₃，a₁₁恰好是某等比数列的前三项，那么该等比数列公比的值等于_____________．

（15）关于直角AOB在定平面a 内的射影有如下判断：①可能是0°的角；②可能是锐角；　 ③可能是直角；④可能是钝角；⑤可能是180°的角．其中正确判断的序号是________________（注：把你认为是正确判断的序号都填上）．

（16）已知P是直线3x＋4y＋8=0上的动点，PA，PB是圆x²＋y²－2x－2y＋1=0的两条切线，A，B是切点，C是圆心，那么四边形PACB面积的最小值为____________．

三、解答题：本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．

（17）（本小题满分12分）

解不等式．

（18）（本小题满分12分）

如图，在多面体ABCD－A₁B₁C₁D₁中，上、下底面平行且均为矩形，相对的侧面与同一底面所成的二面角大小相等，侧棱延长后相交于E，F两点，上、下底面矩形的长、宽分别为c，d与a，b，且a>c，b>d，两底面间的距离为h．

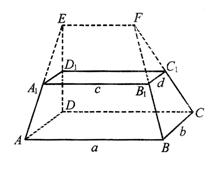
（Ⅰ）求侧面ABB₁ A₁与底面ABCD所成二面角的大小；

（Ⅱ）证明：EF∥面ABCD；

（Ⅲ）在估测该多面体的体积时，经常运用近似公式

V_估=S_中截面·h来计算．已知它的体积公式是

（S_上底面＋4S_中截面＋S_下底面）

试判断V_估与V的大小关系，并加以证明．

（注：与两个底面平行，且到两个底面距离相等的截面称为该多面体的中截面．）

（19）（本小题满分12分）

数列｛x_n｝由下列条件确定：，n∈N．

（Ⅰ）证明：对n≥2，总有；

（Ⅱ）证明：对n≥2，总有；

（Ⅲ）若数列｛x_n｝的极限存在，且大于零，求的值．

（20）（本小题满分12分）

在研究并行计算的基本算法时，有以下简单模型问题：

用计算机求n个不同的数v₁，v₂，…，v_n的和．计算开始前，n个数存贮在n台由网络连接的计算机中，每台机器存一个数．计算开始后，在一个单位时间内，每台机器至多到一台其他机器中读数据，并与自己原有数据相加得到新的数据，各台机器可同时完成上述工作．

为了用尽可能少的单位时间，使各台机器都得到这n个数的和，需要设计一种读和加的方法．比如n=2时，一个单位时间即可完成计算，方法可用下表表示：

机器号	初始时	第一单位时间		第二单位时间		第三单位时间
		被读机号	结　果	被读机号	结　果	被读机号	结　果
1	v1	2	v1＋v2
2	v2	1	v2＋v1

（Ⅰ）当n=4时，至少需要多少个单位时间可完成计算？

把你设计的方法填入下表

机器号	初始时	第一单位时间		第二单位时间		第三单位时间
		被读机号	结　果	被读机号	结　果	被读机号	结　果
1	v1
2	v2
3	v3
4	v4

（Ⅱ）当n=128时，要使所有机器都得到，至少需要多少个单位时间可完成计算？（结论不要求证明）

（21）（本小题满分12分）

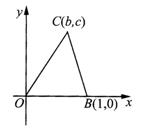
已知O（0，0），B（1，0），C（b，c）是△OBC的三个顶点．

（Ⅰ）写出△OBC的重心G，外心F，垂心H的坐标，并证明G，F，H三点共线；

（Ⅱ）当直线FH与OB平行时，求顶点C的轨迹．

（22）（本小题满分14分）

已知f（x）是定义在R上的不恒为零的函数，且对于任意的a，b∈R都满足：

f（a · b）=af（b）＋bf（a）

（Ⅰ）求f（0），f（1）的值；

（Ⅱ）判断f（x）的奇偶性，并证明你的结论；

（Ⅲ）若（n∈N），，求数列｛u_n｝的前n项的和S_n．

普通高等学校招生全国统一考试数学试题（理工农医类）参考解答

说明：

一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．

二、对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．

三、解答右端所注分数，表示考生正确做到这一步应得的累加分数．

四、只给整数分数．选择题和填空题不给中间分．

一、选择题：本题考查基本知识和基本运算．每小题5分，满分60分．

（1）B　　　　　　　　 （2）D　　　　　　　　 （3）B　　　　　　　　　（4）C

（5）D　　　　　　　　 （6）D　　　　　　　　 （7）C　　　　　　　　　（8）A

（9）A　　　　　　　　 （10）C　　　　　　　 （11）B　　　　　　　　（12）A

二、填空题：本题考查基本知识和基本运算．每小题4分，满分16分．

（13）　　　

（14）4

（15）①②③④⑤　　　　　　　　　　　　　　　　　 （16）

三、解答题:本大题共6小题，共74分．解答应写出文字说明，证明过程或演算步骤．

（17）本小题考查不等式的解法等基本知识，考查运算能力和逻辑思维能力．满分12分．

解：原不等式

因为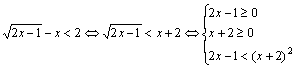　

　

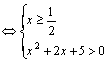
又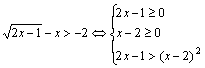　或　

　或　

　或　

　或　

所以，原不等式组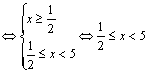

因此，原不等式的解集为

（18）本小题主要考查直线、平面的位置关系，考查不等式的基本知识，考查空间想象能力和逻辑推理能力．满分12分．

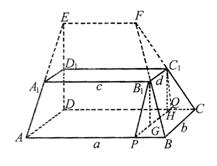（Ⅰ）解：过B₁C₁作底面ABCD的垂直平面，交底面于PQ，过B₁作B₁G⊥PQ，垂足为G．

∵　平面ABCD∥平面A₁B₁C₁D₁，

∠A₁B₁C₁= 90°

∴　AB⊥PQ，AB⊥B₁P．

∴　∠B₁PG为所求二面角的平面角．

过C₁作C₁H⊥PQ，垂足为H．由于相对侧面与底面所成二面角的大小相等，故四边形B₁PQC₁为等腰梯形．

∴　，

又B₁G=h，

∴　，∴,即所求二面角的大小为．

（Ⅱ）证明：∵　AB，CD是矩形ABCD的一组对边，有AB∥CD，

又CD是面ABCD与面CDEF的交线，

∴　AB∥面CDEF．

∵　EF是面ABFE与面CDEF的交线，

∴　AB∥EF．

∵　AB是平面ABCD内的一条直线，EF在平面ABCD外，

∴　EF∥面ABCD．

（Ⅲ）V_估<V．

证明：∵　a>c，b>d，

∴　

∴　V_估<V．

（19）本小题主要考查数列、数列极限、不等式等基本知识，考查逻辑思维能力．满分12分．

（Ⅰ）证明：由x₁=a>0，及，可归纳证明x_n>0（没有证明过程不扣分）．

从而有（n∈N），

所以，当n≥2时，成立．

（Ⅱ）证法一：当n≥2时，因为，

所以　，

故当n≥2时，x_n≥x_n＋1成立．

证法二：当n≥2时，因为，，

所以  ，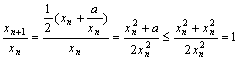

故当n≥2时，x_n≥x_n＋1成立．

（Ⅲ）解：记，则，且A>0．

由　，

得　，

即　．

由  A>0，解得，

故　．

（20）本小题主要考查运用数学思想方法，分析和解决科学问题的能力．满分12分．

（Ⅰ）解：当n=4时，只用2个单位时间即可完成计算．

方法之一如下：

机 器 号	初 始 时	第一单位时间		第二单位时间		第三单位时间
		被读机号	结　果	被读机号	结　果	被读机号	结　果
1	v1	2	v1＋v2	3	v1＋v2＋v3＋v4
2	v2	1	v2＋v1	4	v2＋v1＋v4＋v3
3	v3	4	v3＋v4	1	v3＋v4＋v1＋v2
4	v4	3	v4＋v3	2	v4＋v3＋v2＋v1

（Ⅱ）解：当n=128=2⁷时，至少需要7个单位时间才能完成计算．

（21）本小题主要考查直线与椭圆等基本知识，考查分析问题和解决问题的能力．满分13分．

（Ⅰ）解：由△OBC三顶点坐标O（0，0），B（1，0），C（b，c）（c≠0），可求得

重心，外心，垂心．

当时，G，F，H三点的横坐标均为，故三点共线；

当时，设G，H所在直线的斜率为k_GH，，F，G所在直线的斜率为k_FG．

因为　，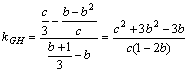

，

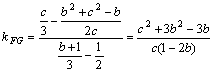所以　，G，F，H，三点共线．

综上可得，G，F，H三点共线．

（Ⅱ）解：若FH∥OB，由，得

配方得　，即．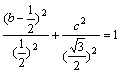

即　．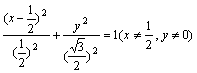

所以，顶点C的轨迹是中心在，长半轴长为，短半轴长为，且短轴在x轴上的椭圆，除去（0，0），（1，0），，，四点．

（22）本小题主要考查函数与数列等基本知识，考查分析问题和解决问题的能力．满分13分．

（Ⅰ）解：f(0)=f（0·0）=0·f（0）＋0·f（0）=0．

因为　f(1)=f（1·1）=1·f（1）＋1·f（1）

所以　f(1)=0．

（Ⅱ）f（x）是奇函数．

证明：因为　f（1）=f〔〕=－f（－1）－f（－1）=0，

所以　，f（－1）=0

f（－x）=f（－1·x）=－f（x）＋xf（－1）=－f（x），

因此，f（x）为奇函数．

（Ⅲ）解法一：由f（a²）=af（a）＋af（a）=2af（a），

f（a³）=a²f（a）＋af（a²）=2a²f（a），

猜测f（aⁿ）=na^n－1f（a）．

下面用数学归纳法证明：

1°．当n=1时，f（a¹）=1·a⁰·f（a），公式成立；

2°．假设当n=k时，f（a^k）=ka^k－1f（a）成立，

那么当n=k＋1时，

f（a^k＋1）=a^kf（a）＋af（a^k）

= a^kf（a）＋ka^kf（a）

=（k＋1）a^kf（a），公式仍成立．

由上两步可知，对任意n∈N，f（aⁿ）=na^n－1f（a）成立．

所以　．

因为　f（2）=2，，

所以　，

（n∈N），

因此　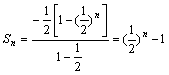（n∈N）．

解法二： 当ab≠0时，

令，则g（a·b）=g（a）＋g（b），

故g（aⁿ）=ng（a），

所以　f（aⁿ）=aⁿ·g（aⁿ）=naⁿg（a）=na^n－1f（a）．

所以　．

（以下同解法一）